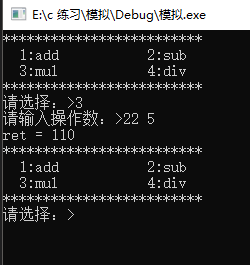
皮尔逊相关系数可以用来表述两个序列的相关性。

常常用来做数据分析、数据挖掘等工作。

如何简单快捷的实现皮尔逊相关，并得到结果？
需要应用MATLAB中的corr(X, Y)或者 corrcoef(X,Y)函数。

其中corr(X, Y)既可以计算矩阵相关也可以计算序列相关，而corrcoef(X,Y)中如果X, Y为矩阵，则会将其转换为序列再进行计算。

CORR

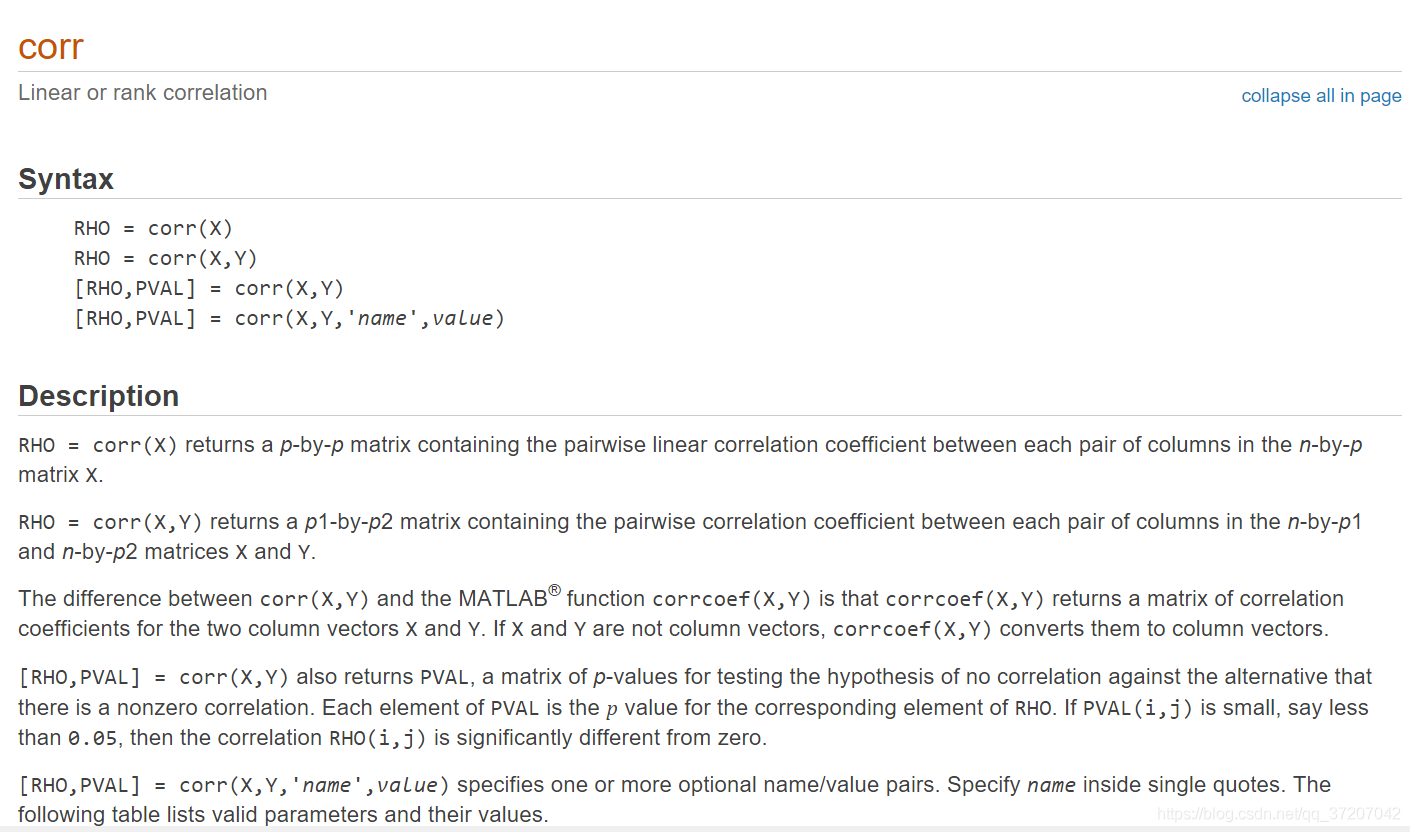
伪代码

X,Y  # 为两个序列并且都是列向量.
pearson_corr = corr(X, Y)   #  求X, Y序列的皮尔逊相关系数.

该函数同样可以设置参数计算不同的相关系数。

'Pearson' (the default) computes Pearson's linear correlation coefficient
'Kendall' computes Kendall's tau
'Spearman' computes Spearman's rho

Example 1

A = randn(10,1);
B = randn(10,1);
R = corrcoef(A,B)
X = corr(A,B)

如果corr()输入为向量则其输出为两个向量相关性的标量系数。

R =1.000000000000000   0.3275140344559130.327514034455913   1.000000000000000
X =0.327514034455913

即R（1，2）= R（2，1）= X

Example 2

rng('default')
x = randn(30,4);
y = randn(30,4);
y(:,4) = sum(x,2); % introduce correlation
[r,p] = corr(x,y)

其中 r 为两个矩阵中列向量间的相关系数，p 为非零相关的假设检验值（位置与 r 对应），如果值小于 0.05 则相关性显著。

r =-0.1686   -0.0363    0.2278    0.69010.3022    0.0332   -0.0866    0.2617-0.3632   -0.0987   -0.0200    0.3504-0.1365   -0.1804    0.0853    0.4908p =0.3731    0.8489    0.2260    0.00000.1045    0.8619    0.6491    0.16240.0485    0.6039    0.9166    0.05770.4721    0.3400    0.6539    0.0059

CORRCOEF

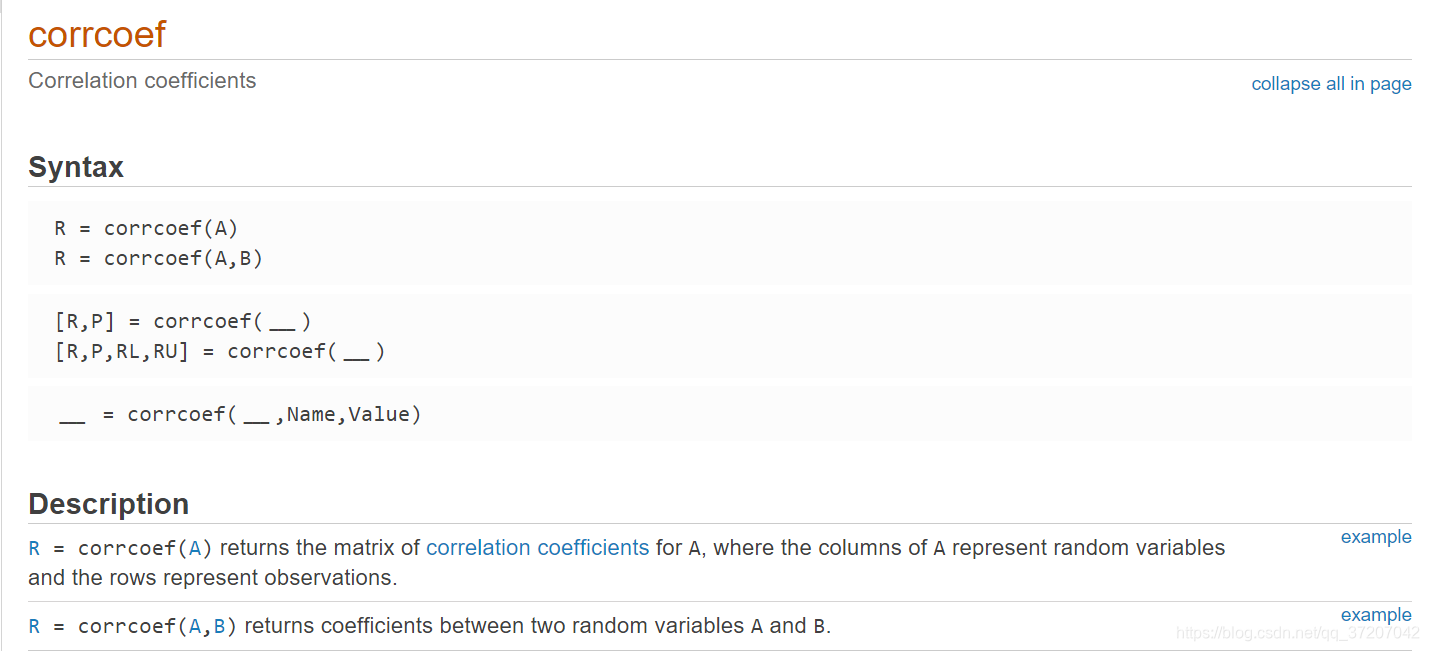
其中corrcoef( )返回的 P 值同样为假设检验值，在corr()中解释过不再解释，详情请见MATLAB帮助文档。

Example 1

x = randn(6,1);
y = randn(6,1);
A = [x y 2*y+3];
R = corrcoef(A)

上述例子中A为（6，3）矩阵，将其每列看作一组变量的序列，进行相关性计算，得到结果

 R = 1.0000   -0.6237   -0.6237-0.6237    1.0000    1.0000-0.6237    1.0000    1.0000

对角线上由于是变量自相关所以都是1，元素(2,3)由于 y 与 2*y+3 是线性相关所以相关系数也是1。

Example 2

A = randn(10,1);
B = randn(10,1);
R = corrcoef(A,B)

上述A,B分别为长度为10的列向量，函数将两个列向量看作两个变量进行相关性分析。

R = 1.0000    0.45180.4518    1.0000