0. 简介
传统的地图生成方法一般是依靠Lidar和IMU结合的,但是问题在于,目前Lidar和IMU的紧耦合主要集中在前端里程计,基本没有涉及到后端全局优化以及建图的融合。为此文章《Globally Consistent and Tightly Coupled 3D LiDAR Inertial Mapping》提出了一种改进的地图生成方法,并设计一个在所有阶段(前端里程计+后端全局优化和建图),IMU和LIDAR都紧耦合的SLAM系统。这是作者实验室的官网,后续应该其后续工作应该会在官网中查到。
Globally Consistent and Tightly Coupled 3D LiDAR Inertial Mapping
1. 文章贡献
本文的LiDAR-IMU紧耦合方法贯穿所有状态估计阶段。是目前为止第一个在全局轨迹规划上同时利用了LiDAR和IMU的约束的工作。与此前的LiDAR-IMU SLAM框架相比有以下几点不同:
- 不同于此前的LiDAR SLAM从点云中提取平面和边缘特征来进行匹配,本文使用体素化的GICP匹配代价因子(voxelized GICP matching cost factor),可以在GPU上并行计算;
- 本方法中的紧耦合里程计模块使用固定滞后平滑;
- 激光雷达和IMU的紧密耦合,这里的紧耦合不仅体现在前端,而且在后端的因子图优化中也大量体现了紧耦合。
2. 详细内容
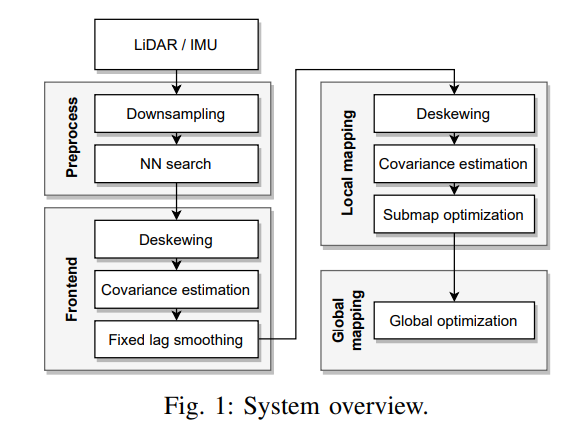
系统框架如下图,主要包括4个模块,预处理模块,前端里程计模块,局部建图模块,全局建图模块,所有模块都是LIDAR-IMU紧耦合的。里程计估计(即前端)模块鲁棒地估计传感器运动,并提供最新传感器状态的初始估计。通过后续的局部映射模块对估计的传感器状态进行细化,并将多个局部帧合并为一个子地图。然后,全局映射模块优化子地图位姿,使全局配准误差最小化,同时保持地图的一致性。我们通过多线程并行运行这些模块。
将在估计模块中被估计的传感器状态 x t x_t xt定义为
x t = [ T t , v t , b t ] T x_t = [T_t, v_t, b_t]^T xt=[Tt,vt,bt]T
其中 T t = [ R t ∣ T t ] ∈ S E ( 3 ) T_t = [R_t| T_t]∈SE(3) Tt=[Rt∣Tt]∈SE(3)为传感器位姿, v t ∈ R 3 v_t∈\mathbb{R}^3 vt∈R3为速度, b t = [ b t a , b t ω ] ∈ R 6 b_t = [b^a_t, b^ω_t]∈\mathbb{R}^6 bt=[bta,btω]∈R6为IMU加速度和角速度偏差。从激光雷达点云 P t P_t Pt和IMU测量值(线性加速度 a t a_t at和角速度 ω t ω_t ωt)估计传感器状态的时间序列。请注意,我们将LiDAR点云转换为IMU坐标框架,并且为了效率和简单性,将它们视为统一的传感器坐标框架。
这部分的具体操作即为进行了一个离群点的剔除,只不过这里离群的定义是依赖于时间戳,由于激光雷达的扫描方法,落入同一个体素格子的点的时间戳应该是大差不差的,用这个时间来做剔除,从而减小噪声点对体素化的负面影响。
2.1 LIDAR匹配残差因子
匹配代价因子约束2个传感器位姿( T i \mathbf{T}_i Ti和 T j \mathbf{T}_j Tj),使点云( P i \mathcal{P}_i Pi和 P j \mathcal{P}_j Pj)之间的匹配代价最小。选择voxelized GICP (VGICP)代价[20]作为匹配代价,它是适用于GPU计算的广义ICP[21]的变体。
VGICP将每个输入点 p k ∈ P i p_k∈\mathcal{P}_i pk∈Pi建模为高斯分布 p k = ( μ k , C k ) p_k = (μ_k, C_k) pk=(μk,Ck),根据当前点 p k p_k pk的邻近点计算协方差矩阵 C k C_k Ck,而上一帧点云 P j \mathcal{P}_j Pj,假设已经经过建图模块融合了的话,则 P j \mathcal{P}_j Pj就已经被体素化,每个体素也是通过一个高斯分布来表示的,这个高斯分布是通过该体素内的所有点的高斯分布计算出来的,当前点云的 p k p_k pk点通过位姿变换:
T i − 1 T j \mathbf{T}^{-1}_i\mathbf{T}_j Ti−1Tj
上一帧点云中的某个体素也符合正态分布:
p k ′ = ( μ k ′ , C k ′ ) p'_k = (μ'_k, C'_k) pk′=(μk′,Ck′)
构成一组数据关联。如果我们把这组数据关联对应的残差记为
d k = μ k ′ − T i − 1 T j μ k d_k=μ'_k-\mathbf{T}^{-1}_i\mathbf{T}_jμ_k dk=μk′−Ti−1Tjμk
然后,基于GICP分布到分布的距离定义 P i \mathcal{P}_i Pi和 P j \mathcal{P}_j Pj之间的匹配代价 e M e^M eM,点云利用体素来实现一个离散化,对落入体素内的点的分布情况进行处理,可以得到内部点的高斯分布,那么按照一般SLAM求位姿的思路,我们的流程大概率是列一个残差的式子,然后寻找一个位姿变化 T T T来最小化这个残差,在GICP里面作者使用的是下面这样一个残差的表示方法。
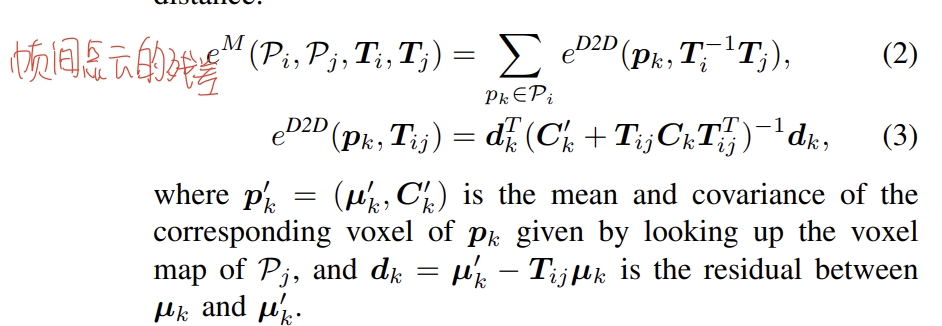
其中 p k ′ = ( µ k ′ , C k ′ ) p'_k =(µ'_k, C'_k) pk′=(µk′,Ck′)是通过查找 P j \mathcal{P}_j Pj的体素图得到的 p k p_k pk对应体素的均值和协方差, d k = µ k ′ − T i j µ k d_k =µ'_k−T_{ij}µ_k dk=µk′−Tijµk是 µ k µ_k µk和 µ k ′ µ'_k µk′之间的残差。
从公式2的导数中,我们得到一个Hessian因子来约束 T i \mathbf{T}_i Ti和 T j \mathbf{T}_j Tj之间的相对姿态。值得强调的是,在每次优化迭代中,都在当前线性化点重新评估和线性化 e M e^M eM, e M e^M eM就是GICP的成本因子,我们可以理解为是总的残差里面的一部分,就像VINS一样。从而得到比传统SE3相对位姿约束[4]更精确的约束。
2.2 IMU的预积分因子
利用IMU预积分技术[22]有效地将IMU约束融入因子图中。给定IMU测量值( a t a_t at和 ω t ω_t ωt),在给定IMU测量的情况下,传感器的未来状态可以估计为:

IMU预积分因子整合了 i i i和 j j j两个时间步间的系统演化,得到了相对的身体运动约束(详细推导参见[22]):
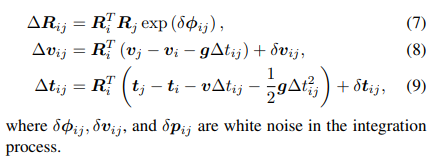
IMU预积分因子使系统能够在几何特征不足且 LiDAR 因子可能不足的环境中保持因子图的良好约束。
3. SLAM pipeline
3.1 数据预处理
这部分中论文作者提到了一个偏移校正的方法,采用时间戳来进行校正。原文的意思个人感觉是给点和体素格子都赋一个时间戳,如果点的时间戳和体素格子的时间戳的偏差超过了一定的范围,就将点移动到另一个体素格子里面去,从而避免在体素进行整合的时候出现明显的偏差。但是论文并没有对这个体素格子的时间戳做说明,个人感觉应该就是进行了一个离群点的剔除,只不过这里离群的定义是依赖于时间戳,由于激光雷达的扫描方法,落入同一个体素格子的点的时间戳应该是大差不差的,用这个时间来做剔除,从而减小噪声点对体素化的负面影响。
3.2 里程计估计
里程计估计模块通过融合LiDAR和IMU测量值来补偿传感器的快速运动,并鲁棒地估计传感器状态。首先,基于IMU动力学的运动预测将点云数据转换到IMU帧,校正传感器运动引起的点云失真;然后,我们使用预先计算的邻近点来计算每个点的协方差。在点的偏移矫正完成之后,按照下图构建因子图。