树的深度和高度

什么是树的深度？什么是树的高度，一张图让你弄明白！我们暂时以二叉树为例。

二叉树的最大高度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

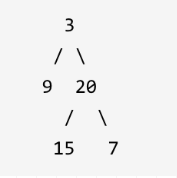
返回它的最大深度 3 。

思路分析

我们在做每一道关于二叉树的题时，都要考虑该用什么遍历方式来解题。

我们要计算一棵树的深度，那么我们就要到达这棵树的最低端，然后在往上数，二叉树的只有左节点和右节点，所以我们只要达到这两者的最低端，然后进行比较即可，所以我们在这里使用后序遍历（左右根）。

递归

如果到现在还不会写递归，请入土吧

class Solution {public int maxDepth(TreeNode root) {if(root == null) return 0;int leftDepth = maxDepth(root.left);int rightDepth = maxDepth(root.right);int depth = 1 + Math.max(leftDepth,rightDepth);return depth;}
}

其实在这里我们可以对代码进行精简，但是我们一定要会上面的代码才行，不要看人家写的简单就抄上去，看两眼看懂了原理，其实根本不懂。

class Solution {public int maxDepth(TreeNode root) {if(root == null) return 0;return 1 + Math.max(maxDepth(root.left),maxDepth(root.right));}
}

迭代

迭代法，我们最适合使用层序遍历了，因为正好最大深度就是层数，若不懂层序遍历，请转博客二叉树的层序遍历。

class Solution {public int maxDepth(TreeNode root) {//root为空，则返回0if(root == null) return 0;//初始化depthint depth = 0;Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);//当队列为空时，跳出while循环while(!queue.isEmpty()){//队列里面存在的节点数int size = queue.size();//每次循环完一层，深度+1depth++;for (int i = 0 ; i < size ; i++) {TreeNode cur = queue.peek();queue.poll();if (cur.left != null) queue.offer(cur.left);if (cur.right != null) queue.offer(cur.right);}}return depth;}
}

层序遍历是一种思想，其实任何一种算法都是一种思想，你可能看了二叉树的层序遍历也并不会写这道题，很正常，代码熟练活，写几道题就可以大体掌握思想了，光靠想不可能会的，即使你会逻辑，你也不会实现。

N叉树的最大深度

什么是N叉树，就是不是二叉树的都是N叉树

例如：

LeetCode.559.N叉树的最大深度

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：3
示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

提示：

树的深度不会超过 1000 。
树的节点数目位于 [0, 104] 之间。

思路分析

其实N叉树的最大深度计算和二叉树没什么区别，就是多了几个子孩子，将几个子孩子都计算一次就可以了，还要注意的一点是，二叉树和N叉树代码写法是不一样的

class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
}

在这里要注意我们是将孩子节点存放在List里面的，那么我们就可以使用List中的方法了，给予我们很多方便。

我们同样可以用递归和迭代来写代码

递归

class Solution {public int maxDepth(Node root) {if (root == null) return 0;int depth = 0;//把每个孩子节点都遍历一遍for (int i = 0 ; i < root.children.size() ; i++) {//这里的size(),get()，使用到了List里面的方法depth = Math.max(depth , maxDepth(root.children.get(i)));}//注意：一定要+1return 1 + depth;}
}

其实这个代码，比二叉树的容易理解多了，不存在怎么前中后

迭代

迭代我们同样使用层次遍历，数层数

class Solution {public int maxDepth(Node root) {if (root == null) return 0;Queue<Node> queue = new LinkedList<Node>();queue.offer(root);int depth = 0;while (!queue.isEmpty()) {int size = queue.size();depth++; for (int i = 0 ; i < size ; i++) {Node cur = queue.peek();queue.poll();//将当前树的所有子节点遍历出来，加入队列for (int j = 0 ; j < cur.children.size() ; j++) {if (cur.children.get(j) != null) queue.offer(cur.children.get(j));}}}return depth;}
}

LeetCode.二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

思路分析

在做最小深度的时候我们需要避免一个误区，我们首先来看下面图例：

这是为什么呢？这就要我们稍微了解一下树的深度的概念了。

• 从根结点到叶子结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。
• 这个叶子节点要注意，是叶节子点，左右孩子都为null的才是叶子结点，所以上图的深度不是1而是3

这也就导致了求最大深度和最小深度的不同，我们需要判断是不是叶子结点。

递归

class Solution {public int minDepth(TreeNode root) {if (root == null) return 0;int leftDepth = minDepth(root.left);int rightDepth = minDepth(root.right);//左子树为空，右子树不为空，说明最小深度为1 + 右子树深度，因为当前节点不是叶子节点//只有当左右子树都为空的节点才是叶子节点if (root.left == null && root.right != null) {return 1 + rightDepth; }//左子树不为空，右子树为空if (root.left != null && root.right == null) {return 1 + leftDepth;}return 1 + Math.min(leftDepth,rightDepth);}
}

一定要记住是，寻找叶子结点，这样你才能理解这个代码！！！

迭代

class Solution {public int minDepth(TreeNode root) {if (root == null) return 0;Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);int depth = 0;//在这里设立一个flag，当找到叶子结点的时候，那说明找到了最小深度boolean flag = true; while(!queue.isEmpty()) {int size = queue.size();depth++;for (int i = 0 ; i < size ; i++) {TreeNode cur = queue.peek();queue.poll();if (cur.left != null) queue.offer(cur.left);if (cur.right != null) queue.offer(cur.right);//如果左右孩子都为null，说明是叶子结点if (cur.left == null && cur.right == null) {flag = false;break;}}//已经找到最小深度，退出//顺便说一句，因为这是层序遍历，所以可以确定是最小深度if (flag == false) break;}return depth;}
}

我们可能有同学想用栈来实现层序遍历，这也不是不可以，但是有点复杂，有兴趣的同学可以尝试一下，面试一般不会这样难为你的，明明有简单的方法为什么要让你用复杂的办法，就算是考你对栈的理解也不会这样考，面试官可能会让用队列实现栈，或者用栈来实现队列。

若有误，请指教！！！