前言
相信通过上一篇文章(顺序表的定义)大家已经能动手定义一个顺序表,并且知道顺序表如何进行初始化的工作。当完成一个顺序表的建立和初始化后,我们得到的会是一个空的顺序表(空表),所以这篇文章我们来学习顺序表的两个基本操作——插入和删除。
顺序表的基本操作——插入
ListInsert(&L,i,e):插入操作。在表L中的第i个位置(位序)上插入指定元素e
- 位序的意思就是按照我们正常生活中的理解,第1位就是第1个,而不是程序语言中的第0位代表第1个
现假设我们用静态分配的方式实现了一个顺序表:
#define MaxSize 10 // 定义最大长度
typedef struct{ElemType data[MaxSize]; // 用静态的“数组”存放数据元素int length; // 顺序表的当前长度
}SqList; // 顺序表的类型定义
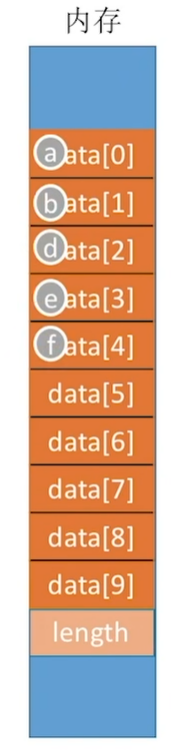
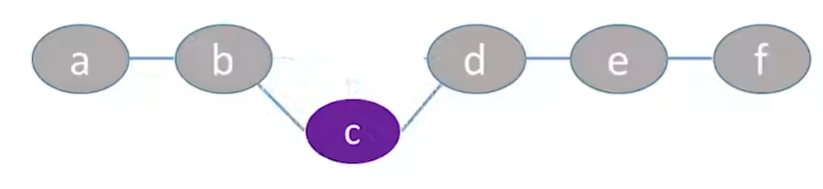
那么在内存中我们看到的应该是这样。

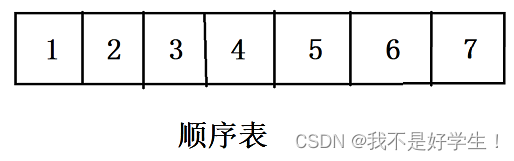
假设现在我们已经存入了5个元素,其在顺序表中存放应该是这样。
如果这时候我们要进行插入操作——在第3个位置插入一个元素c。
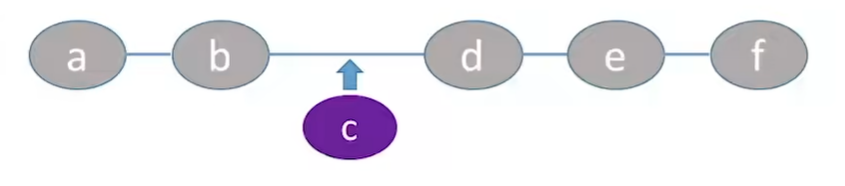
这时候c就应该成为b的后继节点,d的前驱节点。
由于顺序表是通过物理地址的相邻来表示逻辑相邻的元素。
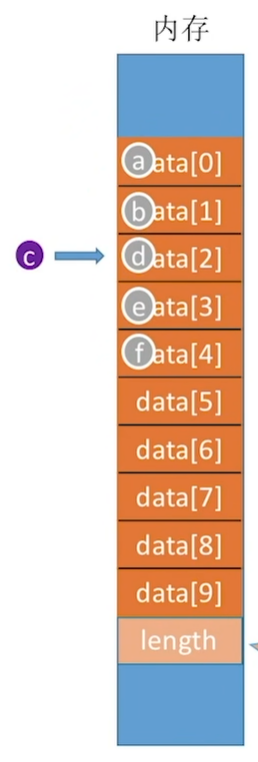
所以这时候就需要将原先处于第3个位置及第3个位置以后的所有元素都后移1位,再将c插入到第3个位置。
广义化
从上述的例子中我们可以得出一个普遍的结论:
- 如果想在第i个位置插入n个元素,那么就要将第i个元素及第i个元素以后的所有元素,向后移n位,然后再以此插入这n个元素
代码实现
注意:我们本篇文章主要以静态分配的方式来实现,当然动态分配也大同小异
在这里我们只书写了部分代码
#define MaxSize 10 // 定义最大长度
typedef struct{int data[MaxSize]; // 用静态的“数组”存放数据元素int length; // 顺序表的当前长度
}SqList; // 顺序表的类型定义void ListInsert(SqList &L,int i,int e){for(int j=L.length;j>=i;j--) // 将第i个元素及之后的元素后移L.data[j] = L.data[j-1];L.data[i-1] = e; // 在位置i处插入e元素L.length++; // 长度+1
}int main(){SqList L; // 声明顺序表InitList(L); // 初始化顺序表// ...省略往顺序表插入元素的过程(你可以假装它满了)ListInsert(L,3,3)return 0;
}
代码分析
声明顺序表和初始化顺序表在上篇文章中已经做了详细的介绍,这里就不再过多介绍,我们直接开始介绍ListInsert()插入函数的操作
- 开头的for循环是顺序表的最后端(最后一个元素)开始将元素后移
- 令j = 顺序表的最后一个元素,每一次移动后j都-1,并且在j<i之后停止循环
- 这里我们用上面的假设:顺序表里已经有5个元素,要在第3个位置插入一个3(
ListInsert(L,3,3):在表L中的第3个位置插入一个元素3) - j = 5(但是我们知道在程序语言中,下标是5相当于表示的是第6个位置)
L.data[j] = L.data[j-1]:将顺序表中第5个位置的元素赋值给第6个元素(就相当于把第5个位置后移至第6个位置)- 以此类推,实现顺序表元素后移的操作。当j=i时,这里就是j=3时,
L.data[j] = L.data[j-1]:将第3个位置的元素赋值给第4个位置。到此第3个位置的元素以及第3个位置往后的元素已经全部后移一位
- 这里我们用上面的假设:顺序表里已经有5个元素,要在第3个位置插入一个3(
- 令j = 顺序表的最后一个元素,每一次移动后j都-1,并且在j<i之后停止循环
- 经过上面的循环后移操作后,第3个位置已经空出,我们直接在第3个位置上插入我们要插入的元素e(赋值为3),上面我们说过由于在程序语言中,是从0开始,所以i=3时表示的是数组中第4个位置,所以要i-1
- 注意这里的虽然第3个位置经过循环后移操作已经空出,但是不代表里面没有数据,这里只是将前一位赋值到后一位,但是前一位的数值仍然存在。当你进行了赋值操作之后,覆盖了原来的数据,才算真正的数据消失(这里听不懂没关系,可能我说的比较抽象,只是为了更加的严谨)
- 由于插入了一个新元素,所以顺序表的长度要+1
问题
这时候已经可以让别人调用自己写的函数实现顺序表的插入功能了,但是我们的代码还是比较的薄弱,仍然还有一些问题,就是可能会存在一些不合法的操作。
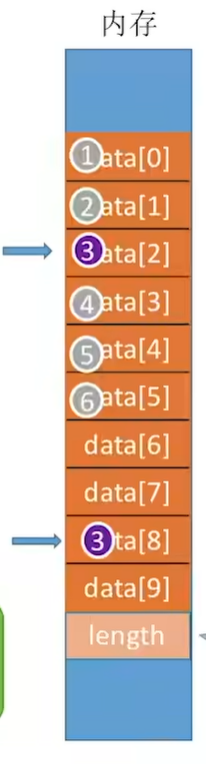
如果此时顺序表中只有6个元素,而你的猪队友想在第9个位置插入元素呢?这显然时不合法的,因为我们知道顺序表是通过物理地址的相邻来表示逻辑位置的相邻,第9个位置插入元素,但是第7和第8的位置上都还没有元素。
这时我们就需要进行插入操作的范围限定。如果我们已经有了6个元素,那么我们可以操作的范围应该是:[1,7](注意这里是使用位序表达, 即1代表第1个位置),也就是[1,length+1]。如果传入的i超出了这个范围,那么我们就不能继续进行下面的操作,所以可以加入一个判断,来判断i是否处于可操作的范围内。
当然,如果当你的顺序表已经插满时,我们也不能在进行插入,所以我们还应该加入一段代码用来检测顺序表是否已经存满,如果已经从存满则不进行下面插入的操作。
反馈
虽然说上面我们考虑到了一些不合法的操作,并且插入了代码检测并且限制。但是不管是哪种不合法的情况,我们都应该要给使用者一些反馈,这样才能让他们知道他们到底是什么操作导致了插入不成功。
所以说我们在写代码的时候除了要保障代码的逻辑正确,此外还要让别人在使用我们代码的时候比较的舒服。比如我们可以在他们可能产生不合法行为的地方返回一些东西,合法行为的地方也返回一些东西。
bool ListInsert(SqList &L,int i,int e){if(i<1 || i>L.length+1) // 判断i的范围是否有效return false;if(L.length>=MaxSize) // 当前存储空间已满,不能插入return false;for(int j=L.length;j>=i;j--) // 将第i个元素及以后的元素后移L.data[j] = L.data[j-1];L.data[i-1] = e; // 在第i个位置插入eL.length++; // 长度+1return true;
}
从以上的代码我们若检测到用户的不合法操作,则返回一个false的布尔值,以告诉使用者你的操作不合法。而在合法执行操作后返回一个true的布尔值来告诉使用者,你的操作合法。按照上述这样的代码才具有”健壮性“
插入操作的时间复杂度
在计算时间复杂度的时候,我们应该是关注最深层循环的执行次数与问题规模n的关系。在这里最深层的循环时将元素后移的语句
for(for(int j=L.length;j>=i;j--))L.data[j] = L.data[j-1];
我们在之前的时间复杂度中说到过如果碰到问题规模相同会有(最好、最坏、平均)的情况:
- 最好情况:新元素插入到表尾,不需要移动元素
- i = n+1 ,循环次数0,最好时间复杂度 = O(1)
- 最坏情况:新元素插入表头,需要将原有的n个元素全部向后移动
- i = 1,循环次数n+1次,最坏时间复杂度 = O(n)
- 平均情况:假设新元素插入到任何一个位置的概率相同,所以 i = 1,2,3,…,length+1的概率 p = 1 n + 1 p=\frac{1}{n+1} p=n+11
- n+1是因为原来有n个元素,但是要插入一个新的元素,所有应该有n+1个元素
- 插入的元素可以插入n个位置中的任意一个位置,也可以插入到表尾(n+1)的位置
- 当i = 1时,循环n次;i = 2时,循环n-1次… i = n+1时,循环0次。故平均循环次数为 n p + ( n − 1 ) p + ( n − 2 ) p + . . . + 1 p = n ( n + 1 ) 2 1 n + 1 = n 2 np+(n-1)p+(n-2)p+...+1p=\frac{n(n+1)}{2}\frac{1}{n+1}=\frac{n}{2} np+(n−1)p+(n−2)p+...+1p=2n(n+1)n+11=2n,平均时间复杂度: O ( n 2 ) − > O ( n ) O(\frac{n}{2})->O(n) O(2n)−>O(n)
在这里我们可以看到,问题规模为n时,执行的次数为n,所以插入操作的时间复杂度为:O(n)
顺序表的基本操作——删除
经过上面的插入学习如果你理解了,其实对于删除操作也就知道的差不多了。
删除的操作则是要将需要删除的位置的元素删除,并且将该位置之后的所有元素前移。
举例
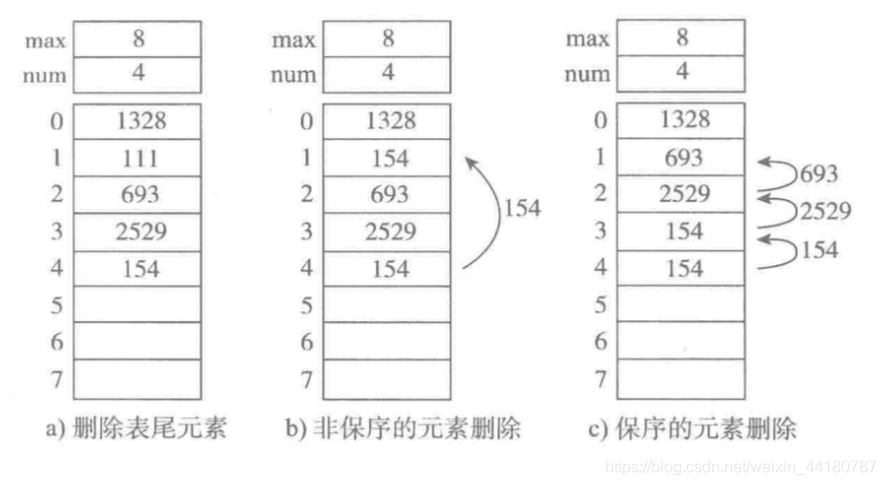
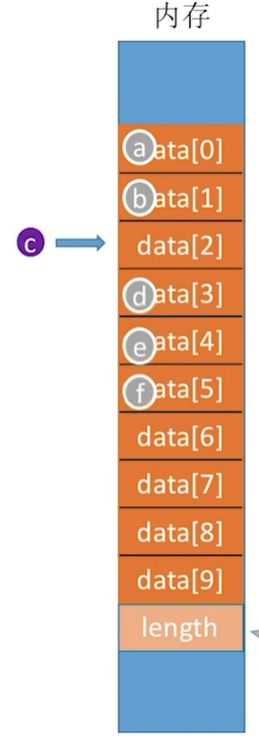
我们要删除c元素
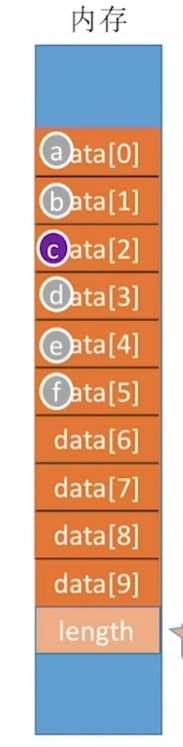
删除c元素
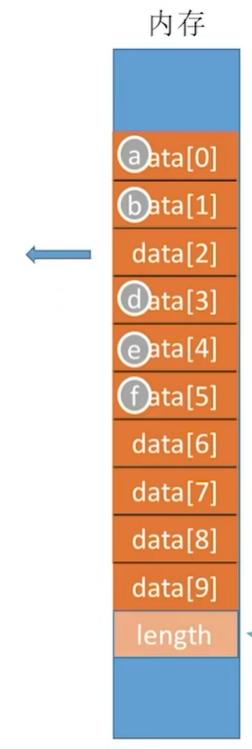
并且将原先c后面的所有元素前移一位

同时要把length的值-1
代码实现
bool ListDelete(SqList &L,int i,int &e){if(i<1 || i>L.length) // 判断i的范围是否有效return false;e = L.data[i-1]; // 将被删除的元素赋值给efor(int j=i;j<L.length;j++) // 将第i个位置的元素前移L.data[j-1] = L.data[j];L.length--;return true;
}int main(){SqList L; // 声明顺序表InitList(L); // 初始化顺序表// ...省略往顺序表插入元素的过程(你可以假装它满了)int e = -1 // 用变量e把删除的元素”带回来“if(ListDelete(L,3,e))printf("已删除第3个元素,删除元素值为=%d\n",e);elseprintf("位序i不合法,删除失败\n");return 0;
}
ListDelete(SqList &L,int i,int &e)
&L:要操作的顺序表i:要删除的位置&e:将删除的值赋值,并且”带回“
代码分析
- 在
main函数中定义了一个int e用来存储删除的元素的值 - 上面我们分析了删除操作的函数参数,e使用了引用,是为了将删除的值带回
- 进入
ListDelete()函数后,首先对i的合法性进行了一个判断,若不合法则返回false- 因为我们要删除的元素肯定是已经有了的元素,所以最大值不能超过length
- 将马上要删除的元素先赋值给e,让e带回
- for循环,将第i个位置(要删除的元素)之后的所有元素前移一位
- 由于是删除操作,元素的数量会减少,顺序表的长度也会减少,所以长度-1
- 操作完成后,返回true
注意:当我们进行插入操作的时候是从后往前,先把后面的元素后移,再后前面的元素。而再删除操作中是从前往后,先将前面的元素前移,再前移后面的元素。
删除操作的时间复杂度
与插入操作相同,删除操作由于是对数组进行操作,故会有(最好情况、最坏情况和平均情况)。
- 最好情况:删除表尾元素,不需要移动其他元素。
- i = n,循环0次。时间复杂度 = O(1)
- 最坏情况:删除表头元素,需要将后面的n-1个元素全部向前移动。
- i = 1,循环n-1次,最坏时间复杂度 = O(n)
- 平均情况:假设删除任意一个元素的概率相同,即i = 1,2,3…length的概率都是 p = 1 n p=\frac{1}{n} p=n1
- 由于删除的元素只有n个,所以概率应为 1 n \frac{1}{n} n1
- i = 1,循环n-1次,i = 2,循环n-2次… i = n时,循环0次
- 平均循环次数 = ( n − 1 ) p + ( n − 2 ) p + . . . + 1 p = n ( n − 1 ) 2 1 n = n − 1 2 (n-1)p+(n-2)p+...+1p=\frac{n(n-1)}{2}\frac{1}{n}=\frac{n-1}{2} (n−1)p+(n−2)p+...+1p=2n(n−1)n1=2n−1,平均时间复杂度 = O ( n − 1 2 ) − > O ( n ) O(\frac{n-1}{2})->O(n) O(2n−1)−>O(n)
结束语
已同步更新至个人博客:https://www.hibugs.net/index.php/sqlistinsndel/
本人菜鸟一枚,仅分享学习笔记和经验。若有错误欢迎指出!共同学习、共同进步 😃
如果您觉得我的文章对您有所帮助,希望可以点个赞和关注,支持一下!十分感谢~(若您不想也没关系,只要文章能够对您有所帮助就是我最大的动力!)
下一篇文章传送门:顺序表的查找