卡方检验(chi-square，记为$\chi^2$检验)是统计学中常用来计数数据分析的方法，对于总体的分布不作任何假设，因此它属于非参数检验法中的一种。本博文从理论到实际应用去阐述卡方检验，最后用python语言去实现卡方分布的代码。

1. 卡方分布

卡方检验是基于卡方分布（(chi-square distribution, $\chi^2$-distribution)的一种假设检验方法，理论证明，实际观察次数（$f_o$）与理论次数（$f_e$），又称期望次数）之差的平方再除以理论次数所得的统计量，近似服从卡方分布。所以首先得说明什么是$\chi^2$分布。

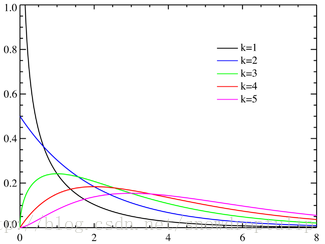
若k个独立的随机变量$Z_1,Z_2,⋯,Z_k$，且符合标准正态分布N(0,1)，则这k个随机变量的平方和

$$X = \sum_1 ^k Z_i ^2$$

为服从自由度为k的卡方分布，记为： X~$\chi^2 (k)$.也可以记为： X∼$\chi^2_k$

卡方分布的期望与方差分别为： E($\chi^2$)=n，D($\chi^2$)=2n，其中n为卡方分布的自由度,一般为样本类别数-1，也就是$n = k-1$。

2. 卡方检验

$\chi^2$检验的基本思想是根据样本数据推断总体的频次与期望频次是否有显著性差异，$\chi^2$的计算公式为：

$$\chi^2 = {(f_o-f_e)^2 \over f_e}$$
其中， $f_o$为实际观察频次， $f_e$为理论值。

这是卡方检验的原始公式，其中当fe越大,近似效果越好。显然fo与fe相差越大，卡方值就越大；fo与fe相差越小，卡方值就越小；因此它能够用来表示fo与fe相差的程度。根据这个公式，可认为卡方检验的一般问题是要检验名义型变量的实际观测次数和理论次数分布之间是否存在显著差异。

一般用卡方检验方法进行统计检验时，要求样本容量不宜太小，理论次数≥5，否则需要进行校正。如果个别单元格的理论次数小于5，处理方法有以下四种：
- a、单元格合并法；
- b、增加样本数；
- c、去除样本法；
- d、使用校正公式。当某一期望次数小于5时，应该利用校正公式计算卡方值。校正公式为：

$$\chi^2 = \sum {(|f_o-f_e|-0.5)^2 \over f_e}$$

3. 应用实例

3.1 独立性检验

独立性检验主要用于两个或两个以上因素多项分类的计数资料分析，也就是研究两类变量之间的关联性和依存性问题。如果两变量无关联即相互独立，说明对于其中一个变量而言，另一变量多项分类次数上的变化是在无差范围之内；如果两变量有关联即不独立，说明二者之间有交互作用存在。

独立性检验一般采用列联表的形式记录观察数据, 列联表是由两个以上的变量进行交叉分类的频数分布表，是用于提供基本调查结果的最常用形式，可以清楚地表示定类变量之间是否相互关联。又可具体分为：

• （1）四格表的独立性检验：又称为2*2列联表的卡方检验。四格表资料的独立性检验用于进行两个率或两个构成比的比较，是列联表的一种最简单的形式。

  • a) 专用公式：
    若四格表资料四个格子的频数分别为a，b，c，d，则四格表资料卡方检验的卡方值=n*(ad-bc)^2/(a+b)(c+d)(a+c)(b+d)，自由度v=（行数-1）*（列数-1）

  • b) 应用条件：
    要求样本含量应大于40且每个格子中的理论频数不应小于5。当样本含量大于40但理论频数有小于5的情况时卡方值需要校正，即公式 $\chi^2 = \sum {(|f_o-f_e|-0.5)^2 \over f_e}$，当样本含量小于40时只能用确切概率法计算概率。

• （2）行x列表资料的独立性检验：又称为RxC列联表的卡方检验。行x列表资料的独立性检验用于多个率或多个构成比的比较。

  • a) 专用公式：
    r行c列表资料卡方检验的卡方值=n*[$(A11/n1n1+A12/n1n2+...+Arc/nrnc)-1$]

  • b) 应用条件：
    要求每个格子中的理论频数T均大于5或$1<T<5$的格子数不超过总格子数的1/5。当有$T<1$或$1<T<5$的格子较多时，可采用并行并列、删行删列、增大样本含量的办法使其符合行x列表资料卡方检验的应用条件。多个率的两两比较可采用行x列表分割的办法。
    独立性检验的理论频数的计算公式为： $f_e = {fxi * fyi \over N}$
    公式中，fxi表示横行各组实际频数的总和；fyi表示纵列各组实际频数的总和；N表示样本容量的总和；

例题：为了解男女在公共场所禁烟上的态度，随机调查100名男性和80名女性。男性中有58人赞成禁烟，42人不赞成；而女性中则有61人赞成，19人不赞成。那么，男女在公共场所禁烟的问题所持态度不同？

kong	赞成	不赞成	行总和
男性	fo11 =58	fo12 =42	R1＝100
女性	fo21 =62	fo22 =18	R2＝80
列总和	C1＝120	C2＝60	T＝180

3.2 2、拟合性检验：

卡方检验能检验单个多项分类名义型变量各分类间的实际观测次数与理论次数之间是否一致的问题，这里的观测次数是根据样本数据得多的实计数，理论次数则是根据理论或经验得到的期望次数。这一类检验称为拟合性检验。其自由度通常为分类数减去1，理论次数通常根据某种经验或理论。

3.3 两种检验的异同：

从表面上看，拟合性检验和独立性检验不论在列联表的形式上，还是在计算卡方的公式上都是相同的，所以经常被笼统地称为卡方检验。但是两者还是存在差异的。

首先，两种检验抽取样本的方法不同。如果抽样是在各类别中分别进行，依照各类别分别计算其比例，属于拟合优度检验。如果抽样时并未事先分类，抽样后根据研究内容，把入选单位按两类变量进行分类，形成列联表，则是独立性检验。
其次，两种检验假设的内容有所差异。拟合优度检验的原假设通常是假设各类别总体比例等于某个期望概率，而独立性检验中原假设则假设两个变量之间独立。

最后，期望频数的计算不同。拟合优度检验是利用原假设中的期望概率，用观察频数乘以期望概率，直接得到期望频数。独立性检验中两个水平的联合概率是两个单独概率的乘积。

4. python 代码

import numpy as np
from scipy.stats import chisquarec1 = np.array([[0.1, 1.1], [6.8, 7.1], [-3.5, -4.1], [2.0, 2.7], [4.1, 2.8],[3.1, 5.0], [-0.8, -1.3], [0.9, 1.2], [5.0, 6.4], [3.9, 4.0]])k = chisquare(c1)
print(k)