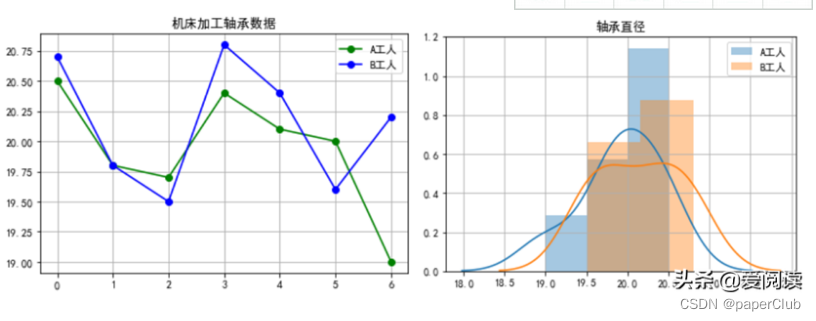
卡方分布是抽样分布的一种。抽样分布其实与概率论中的大数定律有密切的关系。当关注的对象的概率不可知,意味着只知道数据,不知道其内在规律;另一方面,关注的对象是可以分解成多种因素的组合时,就引入了抽样分布。抽样分布是描述从多个随机变量中抽取数据并且加以组合后,形成的规律。基本的抽样分布有三个:x^2(卡方)分布、F分布、t分布。本文介绍卡方分布。
设随机变量X_1,X_2,⋯X_n相互独立,都服从N(0,1),则称
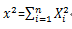
服从自由度为n的 x^2 (卡方)分布,记为x^2 ~x^2(n)(下面直接用卡方分布来代替)。自由度指包含的独立变量的个数。卡方分布是由正态分布构造而成的一个新的分布,当自由度n很大时,卡方分布近似为正态分布。
概率密度函数为:
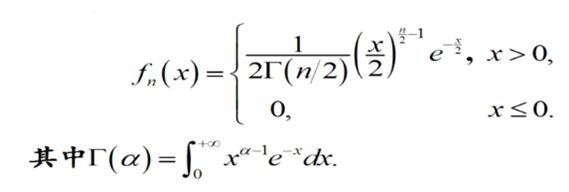
另外一张图来展现卡方分布的概率密度函数和分布函数的规律。

(注:图像来自网络)
因为卡方分布也是一种概率分布,所以概率
卡方分布
article/2025/9/29 21:33:22
相关文章
你还记得吗,超重要的3大抽样分布?
你还记得吗,超重要的3大抽样分布?
原创2022-07-03 21:07爱阅读
三大抽样统计分布是指卡方分布(χ2分布),t分布和F分布,是来自正态总体的三个常用的分布。 1、卡方分布
卡方分布是指符合标准正态分布的样…
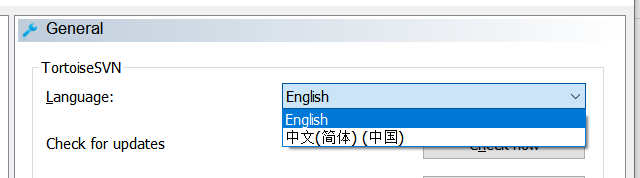
SVN汉化包安装后,没有出现对应的语言选项问题解决(附SVN1.12.1汉化包下载地址)
检查SVN与汉化包的版本是否一致
1、查看tortoise SVN的版本 2、在SVN的安装目录下,将对应版本的汉化包拷过去 注意,保证Languages目录下的文件都已删掉 3、双击安装汉化包,安装完成时,在出现的最后一个页面中,选中Con…
TortoiseSVN安装中文语言包
TortoiseSVN安装中文语言包
1.TortoiseSVN 1.14.0下载地址 下载网址:https://tortoisesvn.net/downloads.zh.html
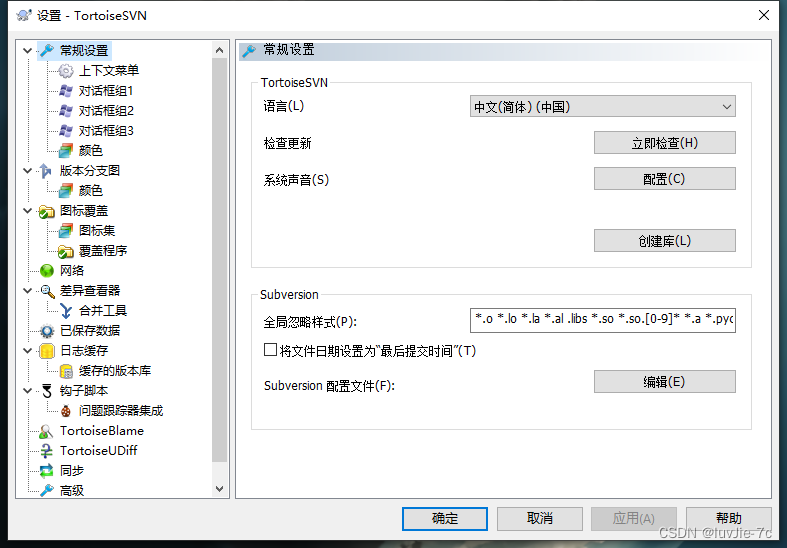
2.安装 直接下一步 3.下载中文安装包 找到安装目录 在桌面空白处右击TortoiseSVN设置
SVN安装语言包后无中文
给svn下载了个语言包,但是安装后无反应,重启了下还是无反应。
后来看了一下svn版本,是12的下载的语言包是11的。就重新下一个版本一样的试试。结果ok了 下载安装ok去选择即可,我的安装后自动就选择了。
版本选择地址https://osd…
SVN:下载、安装和中文设置
一、SVN 下载
步骤1:点击下方链接进入 SVN 下载网址
下载网址:https://tortoisesvn.net/downloads.html
步骤2:点击下载 TortoiseSVN 1.14.3-64-bit 步骤3:点击下载 中文语言包 步骤4:下载完成 二、SVN 安装
步骤1…
解决SVN语言包安装后无法出现下拉框选择
前言:
今天终于有空研究下SVN为啥安装完语言包后无法出现中文下拉框的问题,直接在官网下载语言包安装后也无效。。
看了网上好多教程都是让你删Language目录再安装的,结果也布星。。折磨。。。
然后想了下,干脆去官网对着版本号…
TortoiseSVN 安装中文语言包,SVN中文语言包
SVN中TortoiseSVN 是比较出门的一款SVN软件 TortoiseSVN 是Subversion 版本控制系统的一个免费开源客户端。 由于TortoiseSVN 默认是英文的;所以很多小伙伴可能有压力;那么这次我们来介绍一下怎么样安装中文的语言包 工具/原料 能上网的windows电脑一台 …
TortoiseSVN下载安装及配置中文语言包
目录 一、下载地址
三、安装
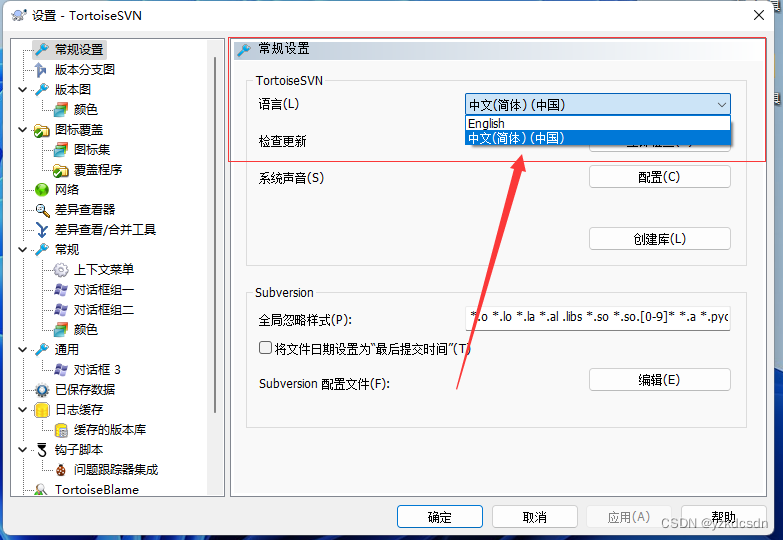
四、更换中文语言包
五、效果 一、下载地址
TortoiseSVN下载
博主提供的SVN资源下载
官网详图: 顺便下个中文语言包64位(页面滚动往下拉就看到了) 二、安装
2个下载包都是傻瓜式安装我就不多说了ÿ…
安装SVN及安装语言包
首先下载SVN程序包,安装SVN----TortoiseSVN-1.10.1.28295-x64-svn-1.10.2.msi。一直单击下一步即可。
安装成功后在下载语言包:https://tortoisesvn.net/downloads.html(语言包和客户端都在这里可以下载) 下载成功后点击安装&…
解决SVN安装语言包后无法选择中文的问题
TortoiseSVN安装后无法选择简体中文,或者安装语言包后也无法选择中文
1、找到 SVN 安装目录,把里面的Languages文件夹删掉 备注:一般svn默认安装路径为:C:\Program Files\TortoiseSVN 2、查看svn的安装版本: 这里我们…
Windows给SVN配置中文语言包
上一篇文章讲了如何下载安装SVN,装的原生的SVN,并没有进行相应的配置,这里进行配置SVN官方语言包 还没有安装的移步安装教程——> Windows搭建SVN实现访问远程SVN库 首先我们打开 svn下载界面(点击可进入) 往下翻即…
下载SVN并设置中文语言
SVN官网:Downloads TortoiseSVNdownload TortoiseSVNhttps://tortoisesvn.net/downloads.html 64位系统安装 下载中文语言包
svn中文语言包安装(内含语言包路径)
一,首先要查看自己电脑安装的svn版本 二,找到和版本相同的svn中文安装包,官方地址 https://tortoisesvn.net/downloads.html
官方是最新的语言包,楼主的1.10.2的语言包是通过如下链接下载的,不需要花费CSDN币&#…
Svn 中文语言包安装
1.中文语言包下载地址,两种下载方式: 下载(1.9.4 版本): https://sourceforge.net/projects/tortoisesvn/files/1.9.4/Language%20Packs/ 官网下载: https://tortoisesvn.net…
svn中文语言安装包使用
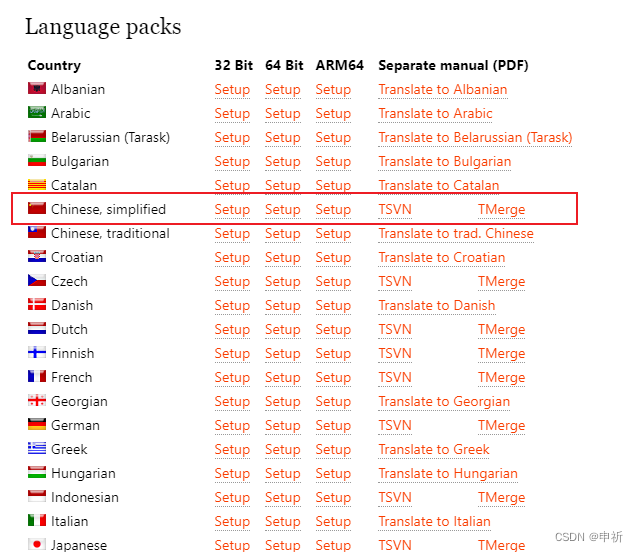
这篇文章介绍svn切换中文语言安装包!!简单易上手 1、找到svn下载官网 https://tortoisesvn.net/downloads.html 这里直接附上 2、滑到language packs这里找到中文,要注意操作系统是32位还是64位 选择合适的下载后在桌面右键打开svn菜单 点…
svn中文语言包安装(最详细步骤)+Language Pack+TortoiseSVN 安装
原文链接:https://blog.csdn.net/massillon/article/details/102780782 svn中文语言包安装(最详细步骤) 一. 查看自己的SVN 版本(这里省略也可以,同事1.9版本的直接在官网下载的语言包也能用,区别对待把,可以先直接在官网下载,不行再去找对应版本语言包) 1.打开SVN找…