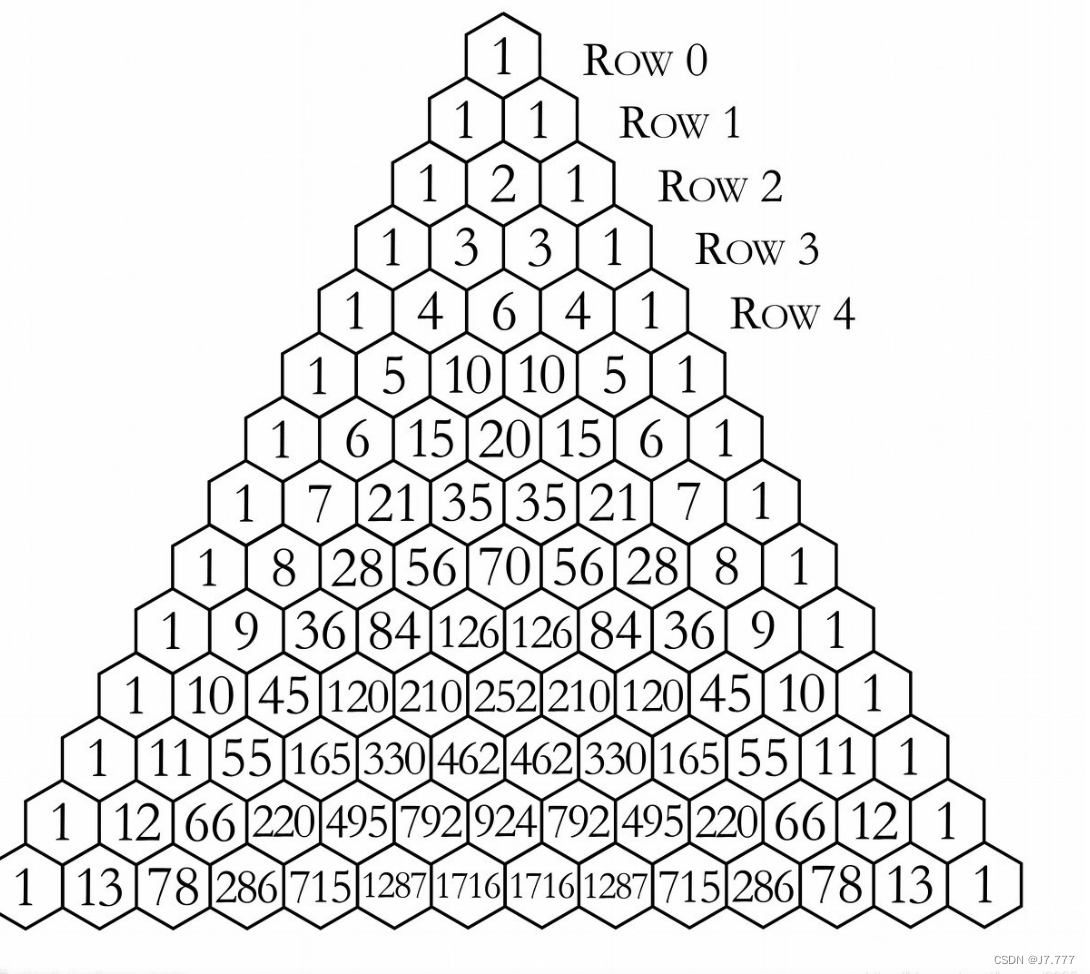
• 杨辉三角，是二项式系数在三角形中的一种几何排列，中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲，帕斯卡（1623 ~ 1662）在1654年发现这一规律，所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年，比贾宪迟600年。

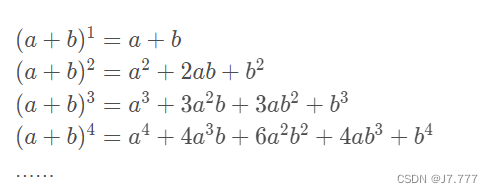
• 二项式定理，又称牛顿二项式定理，由艾萨克牛顿于1664-1665年提出。
  

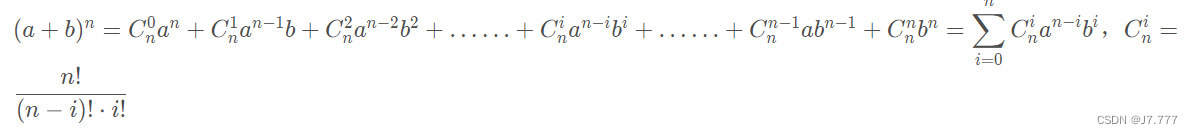
（一）编程实现

• 思路：用二维数组来保存杨辉三角形的元素
  
• 在net.huawei.p02.t08包里创建Task08类
  

public class Task08 {public static void main(String[] args) {// 声明部分（三角形二维数组）int[][] a = new int[15][];// 每行元素个数跟行数一致for (int i = 0; i < a.length; i++) {a[i] = new int[i + 1];}// 边界赋值for (int i = 0; i < a.length; i++) {a[i][0] = 1; // 左边界a[i][i] = 1; // 右边界（对角线）}// 内部元素采用递推公式计算for (int i = 2; i < a.length; i++) {for (int j = 1; j < i; j++) {a[i][j] = a[i - 1][j - 1] + a[i - 1][j];}}// 输出杨辉三角形for (int i = 0; i < a.length; i++) {for (int j = 0; j <= i; j++) {System.out.print(a[i][j] + "\t");}System.out.println();}}
}

• 运行程序，查看结果
  

• 杨辉三角形的数据没有问题，但是格式不好看，需要处理一下，使之显示为三角形。
  

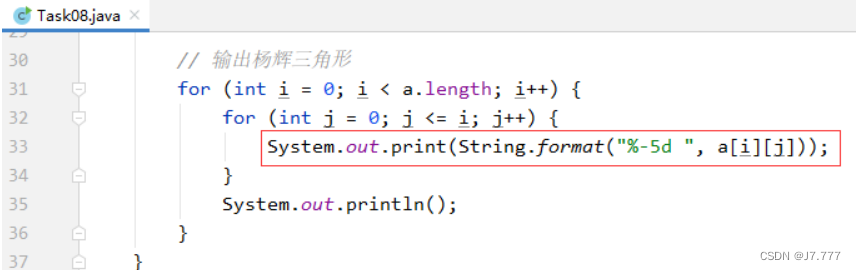
• 再次运行程序，查看结果
  

• 将杨辉三角形显示为等腰三角形
  

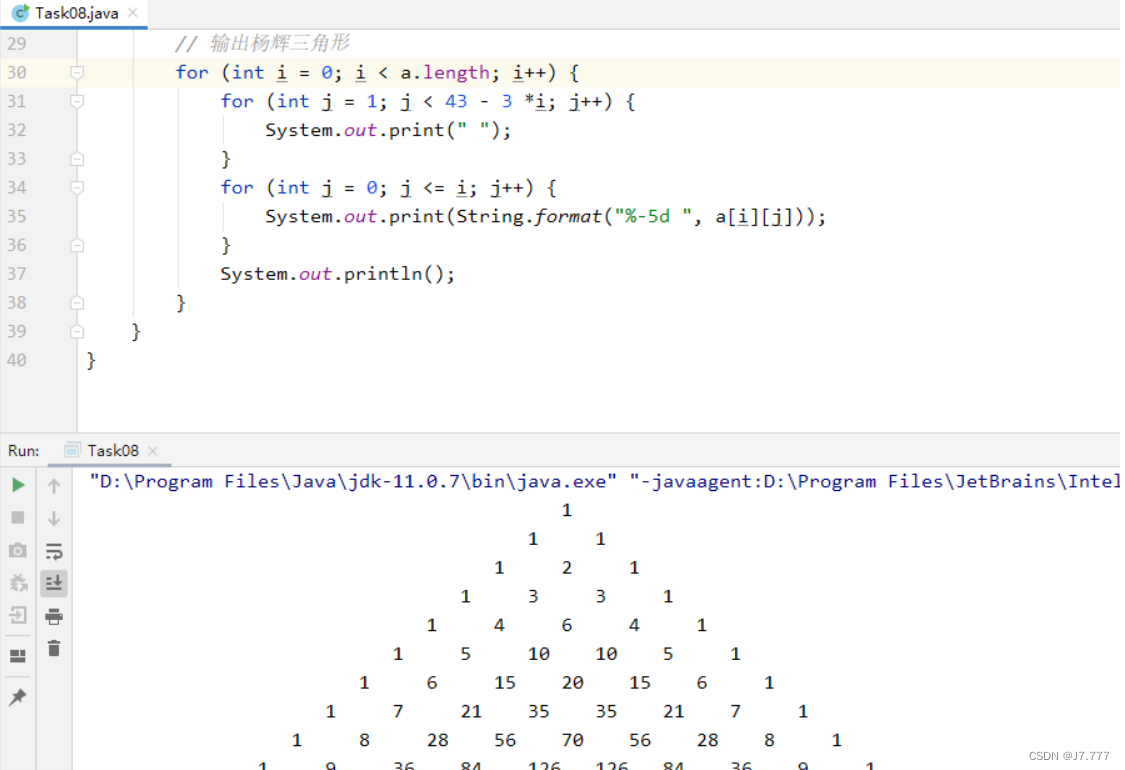
• 利用循环耗时来实现打字机效果
  

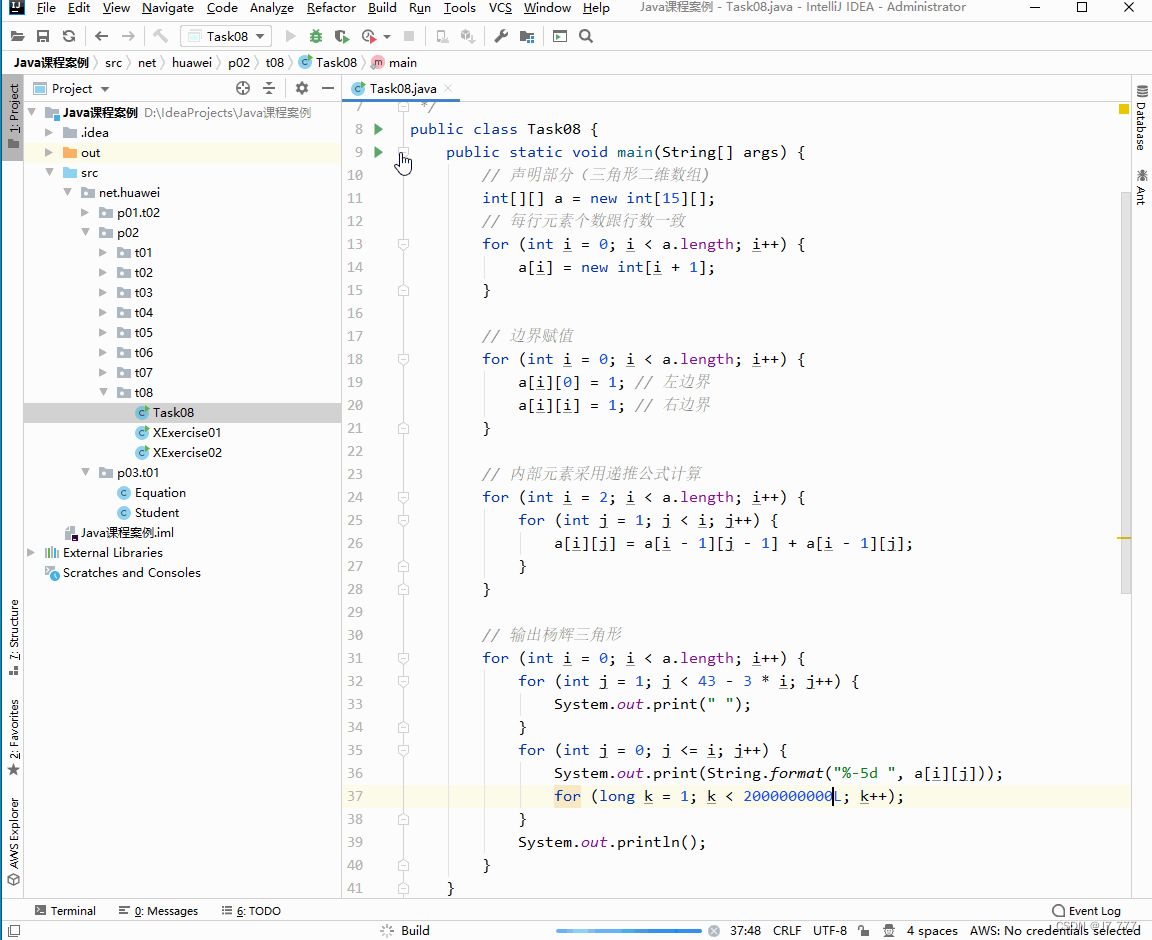
• 这种实现动画效果的方式不好，浪费资源，应该采用多线程来实现动画效果。

（二）讲解知识点

1、指定二维数组行数与列数

int[][] xx = new int[3][4];

• 上面的代码相当于定义了一个3*4的二维数组，这个二维数组的长度为3，可以将它看成3个int[]类型的一维数组，每个一维数组中的元素又是一个长度为4的一维数组。
  

2、指定二维数组行数，不指定列数

int[][] xx = new int[3][];

• 第二种方式和第一种类似，只是数组中每个元素的长度不确定。
  

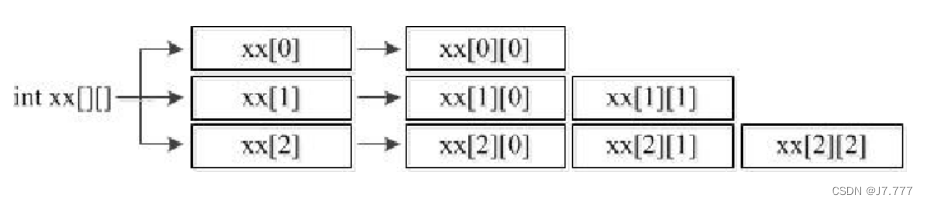
3、直接使用嵌套大括号“{}”静态初始化二维数组

int[][] xx = {{1, 2}, {3, 4, 5, 6}, {7, 8, 9}};

• 上面的二维数组中定义了三个元素，这三个元素都是数组，分别为{1, 2}、{3, 4, 5, 6}、{7, 8, 9} 。
  

（三）拓展练习

任务1、求二维数组最值及位置

• 产生一个3行4列的随机二维数组
  

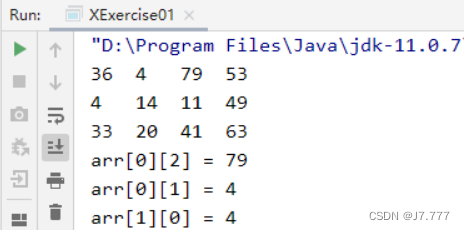
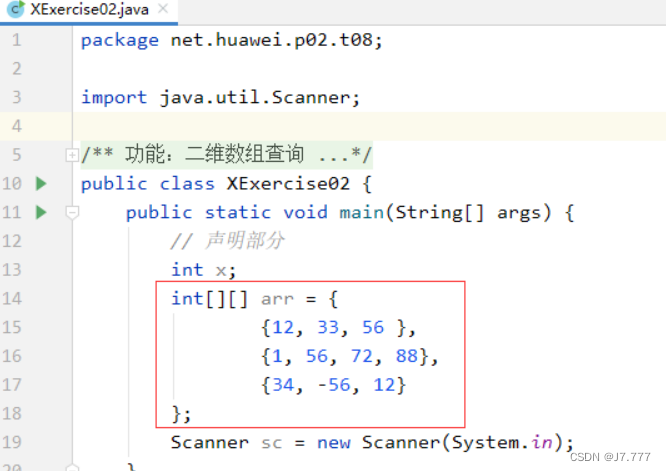
任务2、查询元素是否在二维数组里

• 可以静态初始化一个二维数组