CDF函数(normal distribution)

计算normal distribution拟合下累积分布函数

function [Fncap] = minux_CDF_normal(returns)% Normal cumulative distribution function, the prob. the return% is lower than or equal to the return in cell(i, j) of returns where% assuming returns follow a normal distribution.% input:% returns: matrix of stock returns% output:% Fncap: matrix of cumulative distribution function[n, m]=size(returns);Fncap = zeros(n, m);for j=1:mA = fitdist(returns(:, j), 'Normal'); % 使用正态分布拟合资产收益率for i = 1:nFncap(i, j)=normcdf(returns(i, j), A.mu, A.sigma);endendplot(sort(returns), sort(Fncap));
end

CDF函数(t-location-scale distribution)

The t-location-scale distribution is preferred nub cases of leptokurtosis, as expressed by the distribution¹ of returns(使用t分布可以更好地刻画收益率序列中的尖峰厚尾现象)

给出$T(x,\mu ,\sigma ,\nu )$分布的pdf如下
$$T(x,\mu ,\sigma ,\nu )=\frac{\Gamma (\frac{\nu +1}{2})}{\sigma \sqrt{\nu \pi }\Gamma (\frac{\nu }{2})}[\frac{\nu +(\frac{x-\mu }{\sigma }{)}^2}{\nu }{]}^{-\frac{\nu +1}{2}}$$
由于$\Gamma$结构的存在，所以无法直接计算t-location-scale的CDF，可以使用标准化的方法，转为student t-distribution求解，pdf的转化关系如下
$$T(y,\mu ,\sigma ,\nu )=\frac{1}{\sigma }{\text{PDF}}_{\text{tStudent}}(\frac{y-\mu }{\sigma })$$
得到CDF之间的转化关系
$$F_{tStu}(\frac{y-\mu }{\sigma })=F_{tLoc}(y)$$

function [Ftcap] = minux_CDF_t(returns)% t-location scale cumulative distribution function% in cell(i,j) there is the prob. that the return is lower than or% equal to the return in cell of returns, if returns follow a% t-location scale distribution[n, m] = size(returns);Ftcap = zeros(n, m);for j = 1:mA = fitdist(returns(:, j), 'tLocationScale');for i = 1:nFtcap(i, j)=tcdf((returns(i, j)-A.mu)/A.sigma, A.nu);endendplot(sort(returns), sort(Ftcap));
end

CAPM模型$\beta$计算

CAPM模型
$$E(R_i)=R_f+{\beta }_i[E(R_m)-R_f]+{\epsilon }_i$$
可以使用简单线性回归的方法或者公式法计算${\beta }_i$的值

function [beta] = minux_beta(returns, retmkt)%% generate a column vector that contains the betas of all stocks% input:% returns: matrix of stocks returns% retmkt: column vector of returns of the market% output:% beta: column vector of stocks betas% 回归方法计算m = size(returns, 2);beta = zeros(m, 1);for i=1:mbeta(i, 1)=regress(returns(:, i), retmkt);end% 矩阵方法计算%{cov_mat = cov(returns, retmkt);beta = cov_mat(1, 2)/cov_mat(2, 2);%}
end

误差项${\epsilon }_i$计算

设置误差项${\epsilon }_i$为从如下概率空间抽取的独立随机变量(independent random variables).
$${\epsilon }_i={\sigma }_i{T}_{tStu}({\nu }_i)$$

function [e] = minux_err(returns, retmkt, beta, rf)% generate the error values for the CAPM formula from a process% following an fitted t-Location Scale Distribution% 根据CAPM模型计算误差项% input:% returns: matrix of stocks returns， 资产收益率矩阵% retmkt: matrix of market returns，市场收益率向量% beta，beta列向量% rf，无风险利率% output:% e, matrix of error terms for each stock[n, m] = size(returns);e = zeros(n, m);for i=1:me(:, i) = returns(:, i)-rf-beta(i, 1)*(retmkt-rf);end
end

The expected value of the returns of the market is calculated with the same method as the error term. With all the variables needed, we can simply follow the CAPM formula and calculate the expected returns of security $i$ following a $t$-location scale distribution.

根据$t$分布的性质模拟出场景代码如下

function [rbarStocks] = minux_SCENARIOS(retmkt, beta, rf, e)% this function creates the matrix of predicted returns following the% CAPM% input:% retmkt: matrix of market returns% beta: risk free rate of returns% e: error matrix% output:% rbarStocks: matrix of predicted stocks returns following a t-location% scale[n, m] = size(e);rbarStocks = zeros(n, m);dMarket = fitdist(retmkt, 'tLocationScale'); % 使用t分布拟合市场收益率序列for i = 1:mdErr = fitdist(e(:, i), 'tLocationScale'); % t分布拟合误差序列for j=1:nrbarStocks(j, i) = rf(j, 1)+beta(i, 1)* (random(dMarket)-rf(j, 1))+random(dErr); % 根据拟合市场序列，beta值，误差项生成stock scenariosendend
end

correlation and covariance

One of the major issues related to the use of the CAPM model is the correlation between the predicted returns and the error term. In fact it would mean that the model, with the current structure and variables is not explaining the behavior of returns in a complete way.

计算误差与模拟收益率序列之间的协方差代码如下

function [CovER, Cor] = minux_cov(rbarStocks, e)% input:% rbarStocks: matrix of predicted stock returns% e: matrix of error returns% CovER: 模拟序列和误差项之间的协方差% Cor: 模拟序列和误差项之间的相关系数[n, m] = size(rbarStocks);Cor = zeros(m, 1);for j=1:mA = cov(rbarStocks(:, j)', e(:, j));if j>=2CovER = [CovER; A(1, 2)] ;elseCovER = A(1, 2);endendfor j=1:mCor(j, 1) = corr(rbarStocks(:, j), e(:, j));end
end

$t$分布拟合序列

The prediction of scenarios coherent with the $t-$location scale distribution, without using CAPM.

%% t-分布拟合
rbar_tloc = minux_t_fit(returns);
sample_ret = returns(:, 1);A = fitdist(sample_ret, 'tLocationScale');
xmin = min(sample_ret)-0.01;
xmax = max(sample_ret)+0.01;xp = xmin: 0.01:xmax;
hold on;
yyaxis left; % 激活左轴
yp = pdf(A, xp);
plot(xp, yp, 'b--');
yyaxis right; % 激活右轴
histogram(sample_ret, 'Normalization', 'probability', 'FaceAlpha', 0.4);
legend('t-fitted', 'returns');
hold off;

拟合函数为

function [rbarStocks_tloc] = minux_t_fit(rStocks)[n, m]=size(rStocks);rbarStocks_tloc = zeros(n, m);for j = 1:mA = fitdist(rStocks(:, j), 'tLocationScale'); % 将收益率序列使用t-dist拟合for i=1:nrbarStocks_tloc(i, j)=A.mu+A.sigma*trnd(A.nu);endend
end

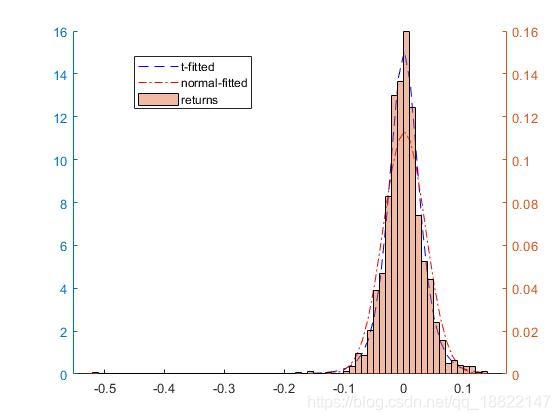
$t$拟合后在双坐标轴上绘制pdf图像，可以发现重合度较高，可以描述收益率尖峰厚尾的现象

对比使用正态分布的拟合图像如下

Generalized Hyperbolic Distribution

广义双曲线分布(GH)的概率密度函数为
$$d_{GH(\lambda ,\alpha ,\beta ,\delta ,\mu )}(x)=a(\lambda ,\alpha ,\beta ,\delta ,\mu )({\delta }^2+(x-\mu {)}^2{)}^{(\frac{2\lambda -1}{4})}{e}^{\beta (x-\mu )}\times K_{\lambda -\frac{1}{2}}(\alpha \sqrt{{\delta }^2+(x-\mu {)}^2})$$
其中，$\alpha >0$为形状参数，偏度由$\beta$的绝对值确定，且$0\le |\beta |<\alpha$，$\mu \in R$为位置参数，$\lambda \in R$刻画尾部形状，$\delta >0$描述尺度参数，正则化函数$a(\lambda ,\alpha ,\beta ,\delta ,\mu )$
$$a(\lambda ,\alpha ,\beta ,\delta ,\mu )=\frac{({\alpha }^2-{\beta }^2{)}^{\frac{\lambda }{2}}}{\sqrt{2\pi }{\alpha }^{(\lambda -\frac{1}{2})}{\delta }^{\lambda }{K}_{\lambda }(\delta \sqrt{{\alpha }^2-{\beta }^2})}$$
其中函数$K_{\lambda }$表示第三种modified Bessel function with index $\lambda$.

GH分布依赖于Generalized Inverse Gaussian Distribution (GIG)，设$\delta \sqrt{{\alpha }^2+{\beta }^2}=\zeta$，GH的期望值为
$$\mathbb{E}(GH)=\mu +\frac{\beta {\delta }^2}{\zeta }\frac{K_{\lambda +1}(\zeta )}{K_{\lambda }(\zeta )}=\mu +\beta \mathbb{E}(GIG)$$

方差为
$$\mathbb{V}(GH)=\frac{{\delta }^2}{\zeta }\frac{K_{\lambda +1}(\zeta )}{K_{\lambda }(\zeta )}+{\beta }^2\frac{{\delta }^4}{{\zeta }^2}(\frac{K_{\lambda +2}(\zeta )}{K_{\lambda }(\zeta )}-\frac{K_{\lambda +1}^2(\zeta )}{K_{\lambda }^2(\zeta )})=\mathbb{E}(GIG)+{\beta }^2\mathbb{V}(GIG)$$

approximation method 1

构造一个严格递增的函数$h(x;\mu )=F_{GH}(x)-\mu$，其中$u$是从$(0,1)$均匀分布中的随机抽样，可以得到数值解
$$h(x;u)={\int }_{\infty }^x{d}_{GH(\lambda ,\alpha ,\beta ,\delta ,\mu )}(x)dx-\mu$$

approximation method 2

根据Newton-Raphson算法近似
$$\{\begin{array}{l}{x}_1\text{start point}\\ x_{k+1}=x_k-\frac{F_{GH}(x_k)-\mu }{d_{GH(\lambda ,\alpha ,\beta ,\delta ,\mu )}}\end{array}$$

Goodness of Fit

Anderson & Darling Test

Anderson & Darling test检测任意分布的公式为
$$AD=\underset{x\in R}{\max }\frac{|F_{emp}(x)-F_{est}(x)|}{\sqrt{F_{est}(x)(1-F_{est}(x))}}$$
其中$F_{emp}(x)$表示empirical CDF，$F_{est}(x)$表示estimated CDF

Kolmogorv Distance

CDF函数差值的绝对值的上界
$$KD=\underset{x\in R}{\sup }|F_{emp}(x)-F_{est}(x)|$$

L1 Distance

$$L_1=\sum _i|F_{emp}(x_i)-F_{est}(x_i)|$$

L2 Distance

$$L_2=\sqrt{\sum _i|F_{emp}(x_i)-F_{est}(x_i){|}^2}$$

References

optimization of Conditional Value-at-Risk

---

1. Location-Scale Distributions ↩︎