目录
一、子图相关概念
1.子图概念
2.点导出子图与边导出子图
点导出子图
边导出子图
3.图的生成子图
二、图运算
1.图的删点、删边运算
删点运算
删边运算
2.图的并运算
3.图的交运算
4.图的差运算
5.图的对称差运算或环和运算
6.图的联运算
7.图的积图
8.图的合成图
三、路与连通性
1.路与圈的相关概念
图中的途径
图中的迹
图中的路
2.连通性
图中两顶点的距离
两顶点的连通性
连通图与连通分支
图的直径
3.连通性性质
定理1 :若图G不连通,则其补图连通
4.偶图判定定理
一、子图相关概念
1.子图概念

简而言之,只要是把一个图的非空部分提取出来,都是该图的子图。
2.点导出子图与边导出子图
点导出子图
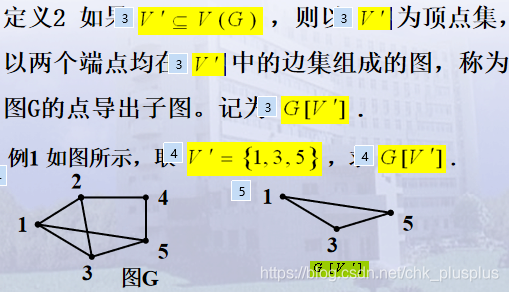
注意:只有两个端点都在定义的点集中的边才会被导出来。
边导出子图
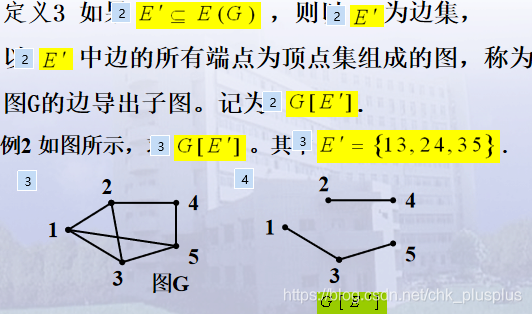
3.图的生成子图

注意:生成子图与原子图顶点数相同,这一点与导出子图略有差异哦
还需要注意,如例子中在求生成子图时,各个顶点已有编号,所以我们是不考虑同构的概念的。
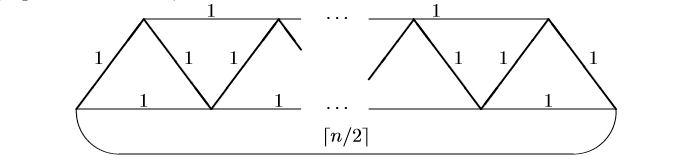
定理:简单图G=(n,m)的生成子图的个数为.
证明:

二、图运算
1.图的删点、删边运算
删点运算

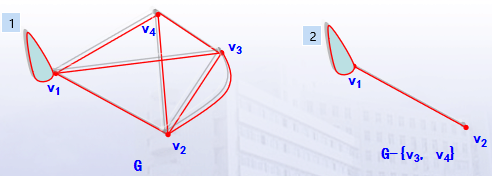
删边运算


删点之后,点和边数目都会变少,而删边之后,点的数目是不会变得!
2.图的并运算
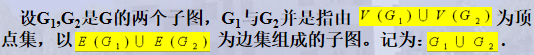

3.图的交运算
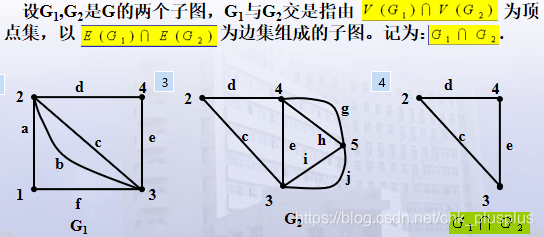
4.图的差运算

注意:差运算不改变被减图的点数!
5.图的对称差运算或环和运算

注意:图的对称差运算用三角形符号表示,对称差等于并减交!
6.图的联运算
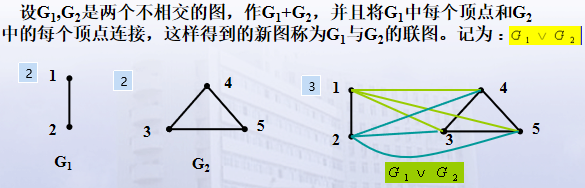
注意:图的联运算用V表示,是两个不相交的图之间的运算,上边定义中+表示直接并,是把两个不相交的图画到一张图里边
7.图的积图
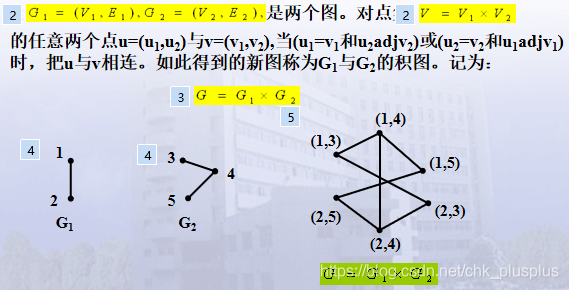
注意:原图中点集都是1维的,积图中点集是二维的,相当于把两个集合的点集做成x轴和y轴,即这里的积是笛卡尔乘积,然后如果第一维元素相等,第二维元素邻接,或,第二维元素相等,第一维元素邻接,则把两个二维的点连起来。
积图中点的度数等于原图中对应两个点的度数之和
8.图的合成图
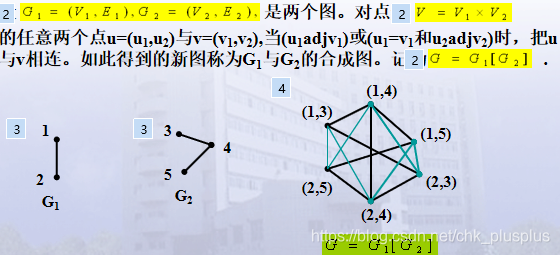
注意:合成图相比于积图来说是把条件放松了,所以连线会更多,第一维的点相等,第二维的点邻接,这个条件是一样的,然后第一维的点只要邻接,也直接相连。合成图的符号是中括号。
三、路与连通性
1.路与圈的相关概念
图中的途径

图中的迹
边不重复的途径称为图的一条迹
图中的路
顶点不重复的途径称为图的一条路
注意:顶点不重复边肯定也不重复,所以路一定也是迹。起点与终点重合是路的一种特殊情况,称为圈。

2.连通性
图中两顶点的距离

两顶点的连通性
![]()
连通图与连通分支

图的直径

连通图的直径是两顶点间的最大距离,非连通图直径为无穷大。
3.连通性性质
定理1 :若图G不连通,则其补图连通
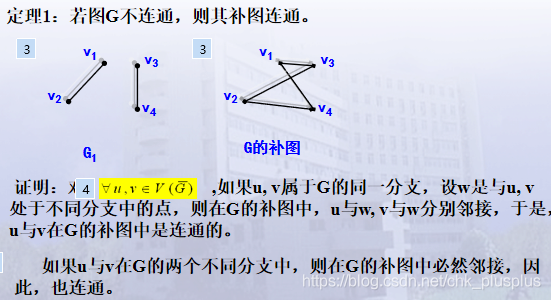
注意反之不一定成立哦,如果一个图连通,并不能推出其补图不连通。
4.偶图判定定理
一个图是偶图当且仅当它不包含奇圈
例题
![]()
证明:
只需要证明在连通图中该结论成立即可,非连通图可以看成若干个连通分支组成
设v1v2......vk-1vk是连通图G中的一条最长路
则vk不存在v1v2......vk-1vk之外的邻接点,否则将产生更长路
又因为vk的度大于等于2
则v1v2......vk-1vk中一定存在vk的邻接点
所以图G一定包含圈
![]()
证明:


证明:
(1)

(2)

![]()
证明:

![]()
证明: