目录
前置
摘要
介绍
模型
应用模型
计算和通信模型
能耗模型
问题定义
NP难
预功率分配算法
能量约束调度
算法1:具有启发式H的能量约束列表调度(ECLS-H)
时间约束调度
算法2:具有启发式H的时间约束列表调度(TCLS-H)
后功率分配算法
能量约束调度
算法3:具有启发式H的能量约束逐级调度(ECLL-H)
时间约束调度
算法4:具有启发式H的时间约束逐层调度(TCLL-H)
前置
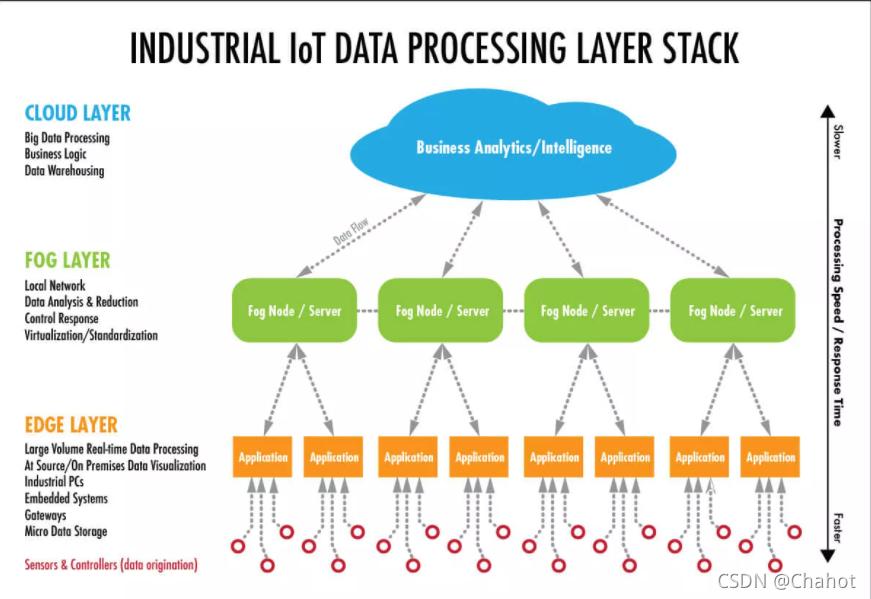
什么是雾计算【来自百度】
雾计算是一种对云计算概念的延伸,它主要使用的是边缘网络中的设备,数据传递具有极低时延。雾计算具有辽阔的地理分布,带有大量网络节点的大规模传感器网络。雾计算移动性好,手机和其他移动设备可以互相之间直接通信,信号不必到云端甚至基站去绕一圈,支持很高的移动性和更多的边缘节点。
| 云计算 | 雾计算 |
| 以IT运营商服务,社会公有云为主的 | 以量制胜,强调数量,不管单个计算节点能力多么弱都要发挥作用 |
| 强调整体计算能力,一般由一堆集中的高性能计算设备完成计算 | 将网络计算从网络中心扩展到了网络边缘,从而更加广泛地应用于各种服务 |
| 几乎全部保存在云中 | 将数据、数据处理和应用程序集中在网络边缘的设备中,数据的存储及处理更依赖本地设备,而非服务器 |
摘要
雾计算环境面临优先级约束、功率分配和性能成本权衡的多重挑战。我们应对这三个挑战的策略描述如下。首先,在功率分配前算法和后功率分配算法中,优先级约束分别由经典列表调度算法和逐级调度方法处理。其次,在功率分配前算法(后功率分配算法)中,在确定计算卸载策略之前(后)确定功率分配策略。第三,通过定义能量约束调度问题和时间约束调度问题来处理性能-成本权衡。
我们开发了一类基于经典列表调度算法和等能量方法的预功率分配算法,用于能量约束和时间约束调度。我们开发了一类用于能量约束和时间限制调度的后功率分配算法,这些算法基于逐级调度方法和我们先前提出的独立任务算法。我们通过对随机生成的有向无环图的移动应用进行广泛实验,对所提出的算法进行了评估,并确定了最有效和最高效的启发式算法。目前没有相关的研究。
介绍
在用户设备(user equipment, UE)上生成的移动应用程序可以分解为具有优先级约束的多个任务,这些任务可以任意复杂。此外,这些任务可能具有非常不同的计算和通信要求。这种复杂的移动应用超出了移动设备用于及时处理的计算能力。
在移动边缘云(mobile edge cloud, MEC)中的服务器的帮助下,可以将移动应用程序的任务卸载到MEC服务器。计算卸载(Computation offloading)提供了增强UE的计算能力并延长UE的电池寿命的有效手段。通过MEC, UE可以在更短的时间内完成应用,而代价是额外的通信时间。UE可以节省用于计算的能量消耗,延长电池使用时间,而代价是用于通信的额外能量。
具有优先约束任务的移动应用的计算卸载成为在雾计算环境中调度移动应用的优先约束任务。雾计算引入了一些与传统节能任务调度系统截然不同的新的独特功能,并且雾计算环境是一个复杂且难以管理的计算平台。首先,UE不将其所有任务卸载到MEC。第二,UE不能改变和控制MEC的计算速度,而只能改变和控制其自身的计算速度和与MEC的通信速度。第三,在处理能量延迟权衡时,仅考虑UE中计算和通信的能量消耗(MECs中的能量消耗不考虑在内)。第四,雾计算表现出强烈的异构性。
在异构雾计算环境中调度移动应用程序的优先级受限任务存在多个挑战。首先,需要确定计算卸载策略,以满足任务之间的所有优先约束。其次,需要确定功率分配策略,对于每个任务,该策略给出本地执行的计算速度或远程执行的通信速度。第三,在定义优化问题时,应考虑性能(即总执行时间)和成本(即总能耗)。
模型
应用模型
假设UE具有移动应用A = (L, ≺)。存在任务列表。每个任务
被指定为
,其中
是
的计算需求(计算量),
是
的通信要求(UE和MEC之间要通信的数据量)。
任务之间存在优先级约束,这些约束由偏序≺指定。如果,则
是
的前身,并且任务
在任务
完成之前不能开始其执行。
具有优先约束任务的移动应用程序可以用有向无环图(dag)G来描述。G中的顶点是L中的m个任务。G中弧的给定方式是,当且仅当时,存在从
到
的弧。
计算和通信模型
假设存在n个异构MEC,即。每个
具有计算速度
(处理器执行速度,不能被UE改变)。
每个任务可以在UE或MEC上执行,任务执行时间包括计算时间和通信时间。
①如果没有卸载并在UE上以计算速度
(可由UE决定)本地执行,则UE上
的计算时间为
。没有用于本地执行的通信时间。
在UE上本地执行的的执行时间为
.
②如果被卸载到
并在
上远程执行,则
上
的计算时间为
。UE与
之间的
的通信速度为
(数据传输速率,可由UE决定)。对于
,UE和
之间的通信时间(以秒为单位)为
。
在上远程执行的
的执行时间为
能耗模型
UE的功耗P中有两个分量用于计算,即动态功耗和静态功耗。
动态分量,其中ξ和α是由该技术确定的一些常数。
静态分量通常是常数
因此,我们得到。
若未卸载并在计算速度为
的UE上本地执行,则功耗为
,并且UE上
的计算能耗为
。
注意,UE除了消耗用于计算的功率之外,还消耗用于通信的功率。
设为任务
的UE到
的传输功率,
, 其中,
是信道带宽,
是各种因素的组合量,如背景噪声功率、其他设备对同一MEC的数据传输对通信信道造成的干扰以及UE和
之间的信道增益。
从UE到的ti通信能耗为
注意,对于UE上的本地执行,仅考虑计算能耗,而对于MEC上的远程执行,只考虑通信能耗。移动应用程序的总能耗为,这是移动应用程序主要的成本度量。
问题定义
移动应用程序A的计算卸载策略(也称为调度)是为每个任务决定何时(执行的开始时间
)和何处(执行的位置,UE或MEC),合法的计划必须确保所有任务遵循优先约束。
若,则有
(前一个任务的开始时间+执行时间 ≤ 下一个任务的开始时间)。功率分配策略是为每个任务ti决定如何执行ti,我们使用T表示完成L中所有任务的总执行时间(即完成时间),这是移动应用程序的主要性能度量。
给定移动应用A=(L,≺) 其中,在具有n个MEC的雾计算环境中(具有计算速度
和能量约束
):
能量约束调度问题是为UE和MEC上的L中的所有任务找到计算卸载策略和功率分配策略,使得E不超过,并且最小化T。
时间约束调度问题是为UE和MEC上的L中的所有任务找到计算卸载策略和功率分配策略,使得T不超过,并且最小化E。
NP难
证明过程暂且忽略
定理1 即使对于独立任务和只有一个MEC,能量约束调度问题也是NP困难的。
定理2 即使对于独立任务和只有一个MEC,时间约束调度问题也是NP困难的。
预功率分配算法
能量约束调度
预功率分配有几种方法。在等速方法中,所有任务具有相同的计算速度。这在雾计算中是不可能的,因为UE不能改变MEC的计算速度。在等时间方法中,所有任务的执行时间相同。这在雾计算中也是不可能的,因为UE只能控制通信时间。
在本文中,我们采用了等能量方法,其中所有任务消耗相同的能量,即。
其优点在于,当在UE或MEC上调度任务时,可以立即确定其计算或通信速度。
①如果没有以计算速度
卸载并在UE上本地执行,则有:
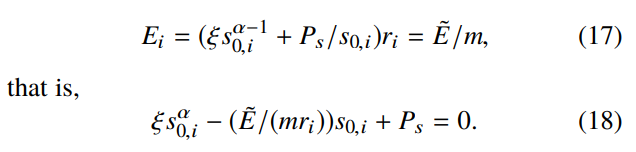
当α = 2时,有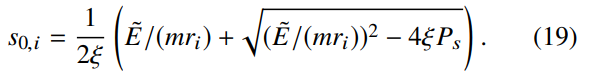
(即
) 。因此,等式(18)可以通过使用标准二分法进行数值求解,在区间
之前搜索最佳
.
后续推理如下述(20)~(22)式所示:【公式(20)暂时没理解如何推出来】
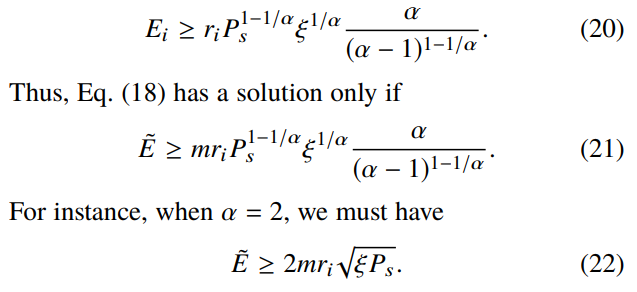
②如果被卸载到
并在
上远程执行,则有:
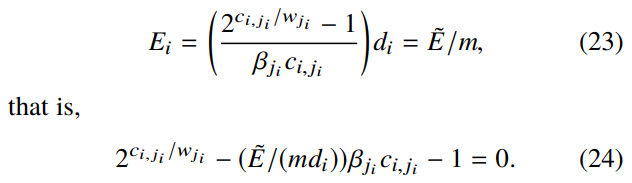
根据泰勒级数(25)我们可推出不等式(26),再根据公式(24)替换即可得出不等式(27),如下所示:
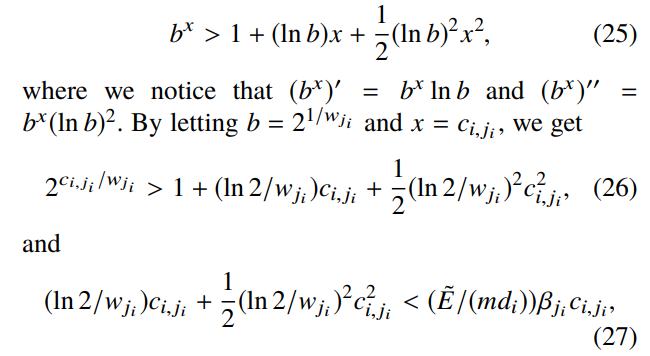
则可以由下述式子表示:
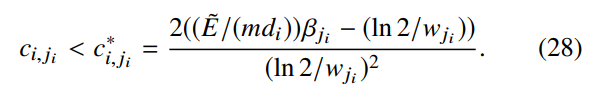
因此,等式(24)可以通过使用标准二分法进行数值求解,在区间之前搜索最佳
,满足公式(29)(30).
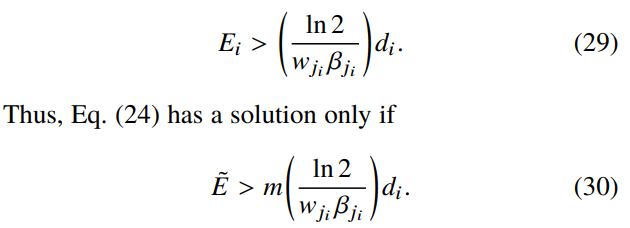
算法1:具有启发式H的能量约束列表调度(ECLS-H)
算法1中介绍了我们的具有预功率分配的能量约束调度算法,称为具有启发式H的能量约束列表调度(ECLS-H)(H参见第5.1节)。
输入:A=(L,≺), 其中,
,
,
和
。
输出:计算卸载策略和功率分配策略,以使E不超过,并使T最小化。
我们将定义为索引j,使得
;
我们将定义为索引j,使得
该算法本质上是适用于雾计算环境的经典列表调度算法[3]。通过预功率分配,当任务计划执行时,任务的执行时间可用。

第1行 用启发式H初始化列表L;
第2行 变量T动态地记录当前时间作为时间表的移动;
第3-9行 for循环在时间0(第(5)行)调度第一批就绪任务(第(3)行)。
第6行 设表示当前在
上运行的任务的剩余执行时间, 为了方便,我们将UE设置为
。
第10-25行 while循环调度剩余任务。在每次重复中,执行以下操作。
第11行 首先,识别最早完成其当前任务的MECj。
第12行 其次,时钟移动到完成当前任务的时刻。
第13-17行 第三,每个繁忙MEC的剩余执行时间(14)由第13-17行中的for循环更新(15)。
第18-24行 第四,下一批就绪任务(18)由第18-24行中的for循环在时间T(20)调度。如果j=0,则(第6和21行)的执行时间为
,其中
通过求解等式(18)找到;如果j>0,则
,其中
通过等式(24)找到。该算法告诉何时何地(第5和20行)以及如何(第6和21行)执行
当等式(18)或等式(24)由于能量分配不足而无法求解时,UE或被认为不可用并被跳过。
算法1的总体时间复杂度为
时间约束调度
算法2:具有启发式H的时间约束列表调度(TCLS-H)
算法2中提出了一种具有预功率分配的时间约束调度算法,称为具有启发式H的时间约束列表调度(TCLS-H)。
输入:A=(L,≺), 其中,
,
,
和
。
输出:计算卸载策略和功率分配策略,以使T不超过,E最小化
当在时间约束调度中调度任务以保证时间约束时,很难确定计算或通信速度。我们的战略是采用两个阶段的过程。
在第一阶段(第1-5行),我们发现使得通过ECLS-H算法获得的T(第3行)不长于
(第5行)。这可以通过将
设置为某个合理值(第1行)并逐渐增加
(第4行)直到
。
在第二阶段(第6-13行),每个任务(第7行)的执行时间按因子(第6行)缩放,通过如下降低计算或通信速度。
如果在UE上(第8行)调度任务,则
被改变为
,使得
,使得
(第9行)。
如果在(第10行)上调度任务
,则
将更改为
,使得
,从而得到
(第11行)。注意,这种执行时间缩放不影响任务之间的优先级约束和执行任务的位置,只影响任务执行的开始时间。
在计算和通信速度降低之后,任务不再消耗相同量的能量。然而,这根本不是问题,因为我们最初的目的是产生计算卸载策略和功率分配策略,以满足时间约束。如果在第一阶段调用ECLS-H算法K次,则算法2的总体时间复杂度为,K值取决于E的初始值和增量∆E。
后功率分配算法
能量约束调度
有向无环图可以分解为v个级别,其中级别定义如下。
1级由初始任务组成,即没有前导任务的任务。如果从某个初始任务到任务的最长路径上的节点数为
,则l级包含任务
;
设表示级别
中的一组任务, 因此,我们有
。
我们采用逐级调度方法,即L中的任务是逐级调度的。这意味着只有当所有在中的任务都完成后,
中的任务才可以开始执行。每个级别的进度表都是单独、独立和分别生成的。整个移动应用程序的调度只是
的v个调度的级联。
算法3:具有启发式H的能量约束逐级调度(ECLL-H)
由于同一级别中的所有任务彼此独立,我们可以通过使用任何启发式能量约束调度算法H对独立任务进行调度。所有这些算法都具有独特的特征,即,在确定计算卸载策略之后确定功率分配策略。算法3中提出了一种具有后功率分配的能量约束调度算法,称为具有启发式H的能量约束逐级调度(ECLL-H)。
逐级能量约束调度的关键问题是确定如何将给定能量预算E~分配给v级。
输入:A =(L, ≺), 其中,
,
,
和
。
输出:计算卸载策略和功率分配策略,以使E不超过,并使T最小化

设为算法H应用于具有能量约束
的
时的总执行时间。
第1-3行 最初,通过使用具有一些初始能量分配El的算法H来调度每个级别Ll。
第4-5行 然后,剩余能量(第4行)除以K得到
(第5行);
第6-16行 while循环重复了略多于K次。在每次重复中,执行以下操作:
第一,确定∆E,它是一个随机数γ乘以E',其中γ均匀分布在[0.5,1.0](第10行)。
第二,在以下情况下,选择导致其总执行时间减少最多,提供额外能量∆E(即)的
级(第12行)。
第三,分配级额外能量∆E(第13行)。在分配了所有剩余能量之后,while循环终止(第6行)。
移动应用程序的总执行时间T为(第17行)。
Ll的初始能量约束El确定如下。定义![]() ,根据下式,我们可以将
,根据下式,我们可以将设置为
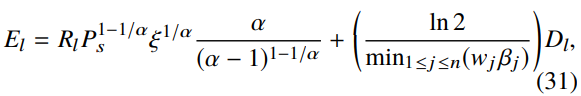
【注】对于同一级别的独立任务,我们的启发式能量约束调度算法H将相同的计算速度分配给在UE上本地执行的所有任务,并将相同的通信速度
分配给
上远程执行的所有工作。然而,来自不同级别的任务具有不同的计算速度,即使它们都在UE上本地执行,而来自不同级别任务具有不同通信速度,即使他们都在同一MEC上远程执行.
算法3的时间复杂度为
时间约束调度
算法4:具有启发式H的时间约束逐层调度(TCLL-H)
算法4中提出了我们的具有后功率分配的时间约束调度算法,称为具有启发式H的时间约束逐层调度(TCLL-H)。
输入:A=(L,≺), 其中,
,
,
和
。
输出:计算卸载策略和功率分配策略,以使T不超过,E最小化

逐级时间约束调度中的关键问题是确定如何将给定的时间预算T分配给v级。
设为算法H应用于具有时间约束
的
时的总能耗。
第1-3行 最初,通过使用算法H和一些初始时间分配Tl来调度每个级别Ll。
第4-5行 然后,附加时间(第4行)除以K得到
(第5行);
第6-16行 while循环重复略多于K次。在每次重复中,执行以下操作:
第一,确定∆T,它是一个随机数γ乘以,其中γ均匀分布在[0.5,1.0](第10行)
第二,选择导致其总能耗增量最小,时间量∆T减少(即)的
级(第12行)
第三,级的执行时间减少了∆T(第13行)。
while循环在所有附加时间减少后终止(第6行)。移动应用程序的总能耗E为(第17行)。
的初始时间约束
确定如下:
![]()
算法4的总时间复杂度为