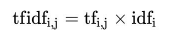机器学习之特征提取
1.为什么要特征提取
原始数据常常是高维的,其中包含了许多冗余信息或者十分稀疏或者计算量大,拿原始数据来训练可行,但是往往直接训练是低效的。所以特征提取往往是必要的。
注:特征提取主要是为了解决下面三个问题,(1)原始数据特征中的强相关性造成的冗余信息。(2)原始数据十分稀疏。(3)原始数据维度巨大。
2.特征提取的主要方法。
- 主成分分析(PCA)
主成分分析是特征提取中的常用方法,用于数据降维,目的是通过线性变换将原始数据变换为一组各维度线性无关的表示,核心思想n维特征映射到k维空间上k<n,这k维特征是全新的正交特征。
核心思想: 最大方差理论,在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,越大越好。因此我们认为,最好的k维特征是将n维样本点变换为k维后,每一维上的样本方差都尽可能的大。
具体思想到推理,给出了一个很好的过程。

PCA算法的优缺点。
- LDA线性判别
详细推导
LDA是将通过投影的方法,投影到维度更低的空间,使得投影后的点,会形成按类别区分,相同类别的点,将会在投影后更接近,不同类别的点距离越远。
LDA的思想是设法将样本投影到一条直线上,使得:
-
同类样本的投影点尽可能近
-
异类样本的投影点尽可能远
-
3. ICA独立成分分析
ICA历史:是20世纪90年代发展起来的一种新的信号处理技术,它是从多维统计数据中找出隐含因子或分量的方法。从线性变换和线性空间角度,源信号为相互独立的非高斯信号,可以看作线性空间的基信号,而观测信号则为源信号的线性组合,ICA就是在源信号和线性变换均不可知的情况下,从观测的混合信号中估计出数据空间的基本结构或者说源信号。
ICA独立成分分析是从多元(多维)统计数据中寻找潜在因子或成分的一种方法.ICA与其它的方法重要的区别在于,它寻找满足统计独立和非高斯的成分。
统计技术如主成分分析(principal component analysis,PCA)、因子分析(factor analysis,FA)的出现,它们是进行统计数据处理、特征提取、数据压缩等比较经典的技术。
寻找矩阵W的另一个统计原理是统计独立性:假设成分yi之间是统计独立的.这意味着其中一个成分没有受到另一个成分的任何影响,成分之间没有任何信息传递.在因子分析中,经常声称因子之间是统计独立的,这个说法只是部分正确,因为因子分析假设因子是服从高斯分布的,找到独立的方法相当容易(对于高斯分布的成分来说,不相关与独立是等价的)。