向量范数
今天来聊一聊机器学习矩阵论的相关知识——范数(Norm)。
在学习机器学习基础算法的推导过程中,可以看到很多地方都应用到了这个范数。范数属于矩阵论的知识范围,可见数学基础的重要性。
机器学习的数学基础重点推荐——MIT的机器学习数学基础课
如果只需要快速了解,请参考——矩阵范数计算
完整的MIT数学基础课程笔记可以参考:MIT 18.06 线性代数笔记
这是个非常棒的手动演算流程,本文也将编码进行验算。
向量范数
定义:一个向量空间V到实数空间的映射,不仅如此,还要满足喜爱额条件:
- ∣ ∣ x ∣ ∣ ⩾ 0 ||x||\geqslant 0 ∣∣x∣∣⩾0,并且 ∣ ∣ x ∣ ∣ = 0 → x = 0 ||x||=0 \rightarrow x=0 ∣∣x∣∣=0→x=0
- 对于任意实数$\gamma , 有 ,有 ,有||\gamma x|| = \gamma ||x||$
- 满足三角不等式, ∣ ∣ x ∣ ∣ + ∣ ∣ y ∣ ∣ ⩾ ∣ ∣ x + y ∣ ∣ ||x||+||y|| \geqslant ||x+y|| ∣∣x∣∣+∣∣y∣∣⩾∣∣x+y∣∣
1-norms
对于向量 V = [ v 1 , v 2 , v 3 , … , v n ] V=[v_1,v_2,v_3,\dots,v_n] V=[v1,v2,v3,…,vn],他的范数是 ∣ ∣ v ∣ ∣ = ∣ v 1 ∣ + ∣ v 2 ∣ + ∣ v 3 ∣ + ⋯ + ∣ v n ∣ = ∑ i = 1 n ∣ v i ∣ ||v||=|v_1|+|v_2|+|v_3|+\dots+|v_n|=\sum_{i=1}^{n}|v_i| ∣∣v∣∣=∣v1∣+∣v2∣+∣v3∣+⋯+∣vn∣=∑i=1n∣vi∣
2-norms(欧几里得范数)
∣ ∣ x ∣ ∣ 2 = v 1 2 + v 2 2 + ⋯ + v n 2 = ∑ i = 1 n v i 2 ||x||_2=\sqrt{v_1^2+v_2^2+\dots+v_n^2}=\sqrt{\sum_{i=1}^{n}v_i^2} ∣∣x∣∣2=v12+v22+⋯+vn2=i=1∑nvi2
p-norms(特别的 ∞ \infty ∞-范数)
∣ ∣ x ∣ ∣ p = ( ∑ i = 1 n ∣ v i ∣ p ) 1 p , a n d p ⩾ 1 ||x||_p=(\sum_{i=1}^{n} |v_i|^p)^{\frac{1}{p} },and \quad p\geqslant 1 ∣∣x∣∣p=(i=1∑n∣vi∣p)p1,andp⩾1
∞ \infty ∞-norms
∣ ∣ x ∣ ∣ ∞ = m a x 1 ⩽ j ⩽ n ∣ x j ∣ ||x||_\infty =max_{1 \leqslant j \leqslant n}|x_j| ∣∣x∣∣∞=max1⩽j⩽n∣xj∣
可视化

还有来自于知乎的数值计算的图:
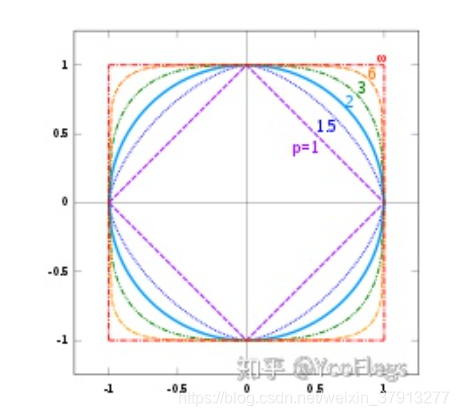
n=2时,令 ∣ ∣ x ∣ p = 1 ||x|_p =1 ∣∣x∣p=1,画出轮廓。p=1时候是菱形,p=2是圆形,p=6是圆角矩形,p=∞是方形。
对于渲染voronoi图或者机器学习的时候,使用不同范数将获得不同的边界。下图展示了离两个固定点距离相同的点组成的边界,范数定义不同,边界也不同。2-范数最简单,一直是垂直平分线,1-范数和∞-范数都存在折线,而且随着两固定点连线和x轴夹角的变化,会出现边界突变的情况。另外,这三个范数绘制的边界都经过2-范数定义的中点。有兴趣可以试下p>2时候的情况。——数值计算:向量和矩阵范数

在我们的机器学习和神经网络最优化问题就经常会使用范数,MIT的老师就给我们举了一个例子:
假设我们要求 c 1 x 1 + c 2 x 2 = 0 c_1x_1+c_2x_2=0 c1x1+c2x2=0,限制条件下 x x x的最小范数:

其中的思想可以理解成,你以任何一种范数对应的图形,从原点开始blow up(增大),直到和限制条件出现交点(hit first),那么久最小的blow up,也就是上式所求最小化问题的答案。
矩阵范数
我觉得理解一样事物应该从感性的角度出发,推荐一个博文——范数的物理意义
其中精髓如下:
- 函数图象联系了函数和几何,表达两个数之间的变化关系,映射推广了函数的概念
- 为了便于研究映射的性质以及数学表达,我们首先需要对映射的对象进行“量化”,取定一组“基”;确定事物在这组基下的坐标,事物同构于我们所熟悉的抽象几何空间中的点,事物的映射可以理解为从一个空间中的点到另一个空间的点的映射,而映射本身也是事物;
- 从一个线性空间到另一个线性空间的线性映射,可以用一个矩阵来表达,矩阵被看线性作映射;
- 矩阵范数反映了线性映射把一个向量映射为另一个向量,向量的“长度”缩放的比例;
- 由矩阵算子范数的定义形式(下面小节的定义公式)可知,矩阵 A A A把向量 x x x映射成向量 A x Ax Ax,取其在向量 x x x范数为1所构成的闭集下的向量 A x Ax Ax范数最大值作为矩阵A的范数,即矩阵对向量缩放的比例的上界,矩阵的算子范数是相容的。
- 由几何意义可知,矩阵的算子范数必然大于等于矩阵谱半径(最大特征值的绝对值),矩阵算子范数对应一个取到向量 A x Ax Ax范数最大时的向量 x x x方向,谱半径对应最大特征值下的特征向量的方向。
- 矩阵的奇异值分解SVD,分解成左右各一个酉阵,和拟对角矩阵,可以理解为对向量先作旋转、再缩放、最后再旋转,奇异值,就是缩放的比例,最大奇异值就是谱半径的推广,所以,矩阵算子范数大于等于矩阵的最大奇异值,酉阵在此算子范数的意义下,范数大于等于1。此外,不同的矩阵范数是等价的。
通过向量定义的矩阵范数
∣ ∣ A ∣ ∣ p = m a x x ≠ 0 ∣ ∣ A x ∣ ∣ p ∣ ∣ x ∣ ∣ p = m a x ∣ ∣ x ∣ ∣ p = 1 ∣ ∣ A x ∣ ∣ p = σ 1 ||A||_p =\ max_{x \neq 0} \frac{||Ax||_p}{||x||_p}= \ max_{||x||_p=1}||Ax||_p= \ \sigma_1 ∣∣A∣∣p= maxx=0∣∣x∣∣p∣∣Ax∣∣p= max∣∣x∣∣p=1∣∣Ax∣∣p= σ1
这个 σ 1 \sigma_1 σ1是最大的奇异值,那么哪个是x?
如果x是个特征函数,那么他们的比例其实就是特征值 λ \lambda λ,所以他不是特征向量,而是奇异值向量 v 1 v_1 v1。
矩阵 2-范数
矩阵2-范数: ∣ ∣ A ∣ ∣ 2 = λ m a x ( A 2 A ) ||A||_2 = \sqrt{\lambda_max(A^2A) } ∣∣A∣∣2=λmax(A2A) ,为 A T A A^TA ATA的最大特征值,取其对应的特征向量 x x x ,有 A T A x = λ m a x ( A T A ) x = ∣ ∣ A ∣ ∣ 2 2 x A^TAx = \lambda_{max}(A^TA)x= \ ||A||^2_2x ATAx=λmax(ATA)x= ∣∣A∣∣22x 。
所以, A T A x = ∣ ∣ A ∣ ∣ 2 2 x A^TAx =||A||^2_2x ATAx=∣∣A∣∣22x
对 ∣ ∣ A ∣ ∣ 2 2 x ||A||_2^2x ∣∣A∣∣22x取1-范数:
∣ ∣ ( ∣ ∣ A ∣ ∣ 2 2 x ) ∣ ∣ 1 = ∣ ∣ A T A x ∣ ∣ 1 ⩽ ∣ ∣ A T ∣ ∣ 1 ∣ ∣ A ∣ ∣ 1 ∣ ∣ x ∣ ∣ 1 = ∣ ∣ A ∣ ∣ ∞ ∣ ∣ A ∣ ∣ 1 ∣ ∣ x ∣ ∣ 1 ||\ (||A||^2_2x)||_1 \ = \ ||A^TAx||_1 \leqslant ||A^T||_1||A||_1||x||_1=\quad ||A||_\infty||A||_1||x||_1 ∣∣ (∣∣A∣∣22x)∣∣1 = ∣∣ATAx∣∣1⩽∣∣AT∣∣1∣∣A∣∣1∣∣x∣∣1=∣∣A∣∣∞∣∣A∣∣1∣∣x∣∣1
∣ ∣ ( ∣ ∣ A ∣ ∣ 2 2 x ) ∣ ∣ 1 = ∣ ∣ A ∣ ∣ 2 2 ∣ ∣ x ∣ ∣ 1 ⩽ ∣ ∣ A ∣ ∣ ∞ ∣ ∣ A ∣ ∣ 1 ∣ ∣ x ∣ ∣ 1 ||(||A||^2_2x)||_1 = ||A||_2^2||x||_1 \leqslant ||A||_\infty||A||_1||x||_1 ∣∣(∣∣A∣∣22x)∣∣1=∣∣A∣∣22∣∣x∣∣1⩽∣∣A∣∣∞∣∣A∣∣1∣∣x∣∣1
∣ ∣ A ∣ ∣ 2 2 ⩽ ∣ ∣ A ∣ ∣ ∞ ∣ ∣ A ∣ ∣ 1 ||A||_2^2 \leqslant||A||_{\infty}||A||_1 ∣∣A∣∣22⩽∣∣A∣∣∞∣∣A∣∣1
Frobenius范数
∣ ∣ A ∣ ∣ F = ( ∑ i ∑ j ∣ a i j ∣ 2 ) 1 2 ||A||_F= (\sum_{i} \sum_{j} |a_{ij}|^2)^{\frac{1}{2}} ∣∣A∣∣F=(i∑j∑∣aij∣2)21
其中对 A A A进行SVD,得到 A = U Σ V T A=U \Sigma V^T A=UΣVT,可以看出 A A A的Forbenius范数,其实就是进行SVD的 Σ \Sigma Σ的范数。然后就产生了一个新的范数 ∣ ∣ A ∣ ∣ N ||A||_N ∣∣A∣∣N:
∣ ∣ A ∣ ∣ N = σ 1 2 + σ 2 2 + ⋯ + σ n 2 ||A||_N = \sqrt{\sigma_1^2+\sigma_2^2+\dots+\sigma_n^2} ∣∣A∣∣N=σ12+σ22+⋯+σn2
Practise:实践是检验真理的为唯一标准!
对于开头提到的博客,其中进行手算的矩阵norms,本文使用python的numpy进行计算,方便对于每一个计算中间过程进行检查和查看:
print("验证博客手算结果:https://blog.csdn.net/codinghappiness/article/details/90896632")
print("待求矩阵A为:")
A = np.matrix('-1,,5,-2;-2,1,0;3,-8,2')
print(A)print("矩阵A的1范数:")
print (np.linalg.norm(A,ord=1))print("矩阵A的2范数:")
print (np.linalg.norm(A,ord=2))print("以下是分步的计算过程进行验证:")
#print(A.T)
print("A转置A的结果是B:")
B = A.T.dot(A)
print(B)
print("求得特征值:")
e, v = np.linalg.eig(B)
print(e)
print("其中最大得为:")
print(e[0])
print("开平方:")
print(math.sqrt(e[0]))
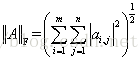










![[魔方]魔方七步初级教程](https://img-blog.csdn.net/20131217212341875?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvZHVidXFpbmdmZW5nZ3p5/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)