目录
牛客 CM11 链表分割
牛客 OR36 之链表的回文结构
Leetcode 160. 相交链表
LeetCode 141. 环形链表
LeetCode 138. 复制带随机指针的链表
本文继续延续前文,为大家带来几道经典的链表中等难度的题目。
牛客 CM11 链表分割
现有一链表的头指针 ListNode* pHead,给一定值x,编写一段代码将所有小于x的结点排在其余结点之前,且不能改变原来的数据顺序,返回重新排列后的链表的头指针。
思路:如果我们在原来的链表上进行操作非常麻烦,可以新建两个链表,分别包含大于x 的结点和小于x 的结点。最后将两个链表合并即可,只需要注意一个问题,就是不要让他们成环,前面结点的指针都会根据大于或者小于x 来进行修改,成环的点在于大于x 的结点组成的链表的最后一个结点的指向,一定要置空,否则会成环。
我的解法:
/*struct ListNode {int val;struct ListNode *next;ListNode(int x) : val(x), next(NULL) {}};*/class Partition {public:ListNode* partition(ListNode* pHead, int x) {ListNode* pBiggerHead = new ListNode(-1);//哨兵头结点ListNode* pLowerHead = new ListNode(-1);//哨兵头结点ListNode* pBiggerCurr = pBiggerHead;ListNode* pLowerCurr = pLowerHead;while(pHead){if(pHead->val < x){pLowerCurr->next = pHead;pLowerCurr = plc->next;}else{pBiggerCurr->next = pHead;pBiggerCurr = pBiggerCurr->next;}pHead = pHead->next;}pLowerCurr->next = pBiggerHead->next;pBiggerCurr->next = nullptr;return pLowerHead->next;}};
牛客 OR36 之链表的回文结构
描述:
对于一个链表,请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法,判断其是否为回文结构。
给定一个链表的头指针A,请返回一个bool值,代表其是否为回文结构。保证链表长度小于等于900。
测试样例:
1->2->2->1返回:true
思路:首先找到中间结点;将中间结点后半部分倒置;分别从头结点和尾结点向中间遍历,检测在达到中间时刻之间val的值是否都相等。所以我们需要用上之前写的题目,先找到中间结点,然后从中间结点开始逆置,就会形成如下的形状。
1 -> 2 -> 3 <- 2 <- 1
/*struct ListNode {int val;struct ListNode *next;ListNode(int x) : val(x), next(NULL) {}};*/class PalindromeList {public:struct ListNode* middleNode(struct ListNode* head) {ListNode* dummy = new ListNode(-1);dummy->next = head;struct ListNode* fast = dummy;struct ListNode* slow = dummy;while (fast) {slow = slow->next;if (fast->next)fast = fast->next->next;elsereturn slow;}return slow;}struct ListNode* reverseList(struct ListNode* head) {struct ListNode* cur = head;struct ListNode* pre = nullptr;struct ListNode* next = nullptr;while (cur) {next = cur->next;cur->next = pre;pre = cur;cur = next;}return pre;}bool chkPalindrome(ListNode* A) {ListNode* midNode = middleNode(A);ListNode* tailNode = reverseList(midNode);while(A != midNode){if(A->val != tailNode->val) return false;A = A->next;tailNode = tailNode->next;}return true;}};
Leetcode 160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
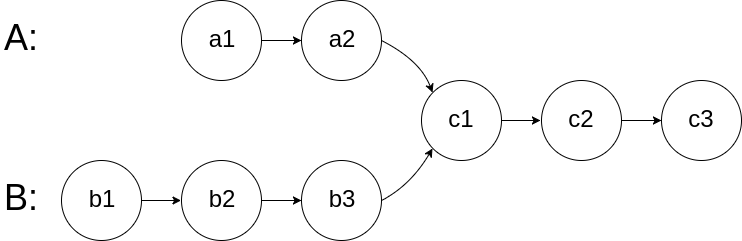
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
思路:本题的难度在于两个单链表的长度未知,而且关系未知,就是有可能等长,有可能不等长。我们可以知道如果A链表长度为a,B链表长度为b,我们可以先遍历一遍,寻找到A 和B 链表的长度的差值 |a-b|,然后让长的先走差值,然后再开始比较。
我的解法1:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/class Solution {public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {if(!headA || !headB) return nullptr;int lengthA = 0;int lengthB = 0;ListNode* currA = headA;ListNode* currB = headB;while(currA){lengthA++;currA = currA->next;}while(currB){lengthB++;currB = currB->next;}currA = headA;currB = headB;if(lengthA > lengthB){//A 先走int dif = lengthA - lengthB;while(dif--){currA = currA->next;}}else if(lengthA < lengthB){int dif = lengthB - lengthA;while(dif--){currB = currB->next;}}int less = lengthA > lengthB ? lengthB : lengthA;while(less--){if(currA == currB){return currA;}else{currA = currA->next;currB = currB->next;}}return nullptr;}};
我的解法2:
上一种解法总体来说还是比较繁琐的,我们可以采用更简单的双指针法,可以假设A 长度为m, B 长度为n,如果相交,A 和 B相交片段长度为 x, 不相交的片段长度分别为a 和b。
那么如果我们采用双指针法:
当链表 headA 和 headB 都不为空时,创建两个指针 pA和 pB,初始时分别指向两个链表的头节点 headA 和 headB,然后将两个指针依次遍历两个链表的每个节点。具体做法如下:
-
每步操作需要同时更新指针 pA 和 pB。
-
如果指针 pA不为空,则将指针 pA 移到下一个节点;如果指针 pB不为空,则将指针 pB 移到下一个节点。
-
如果指针 pA为空,则将指针 pA 移到链表 headB的头节点;如果指针 pB 为空,则将指针 pB 移到链表 headA 的头节点。
-
当指针 pA 和 pB 指向同一个节点或者都为空时,返回它们指向的节点或者 null。
那么如果二者相交,则 m = a + x, n = b + x。pA 和 pB 一定在走过 a + b + x 长度时相等。如果二者不相交,则一定不会出现相等(可以分类讨论)。
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/class Solution {public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {ListNode* pA = headA;ListNode* pB = headB;while(pA != nullptr || pB != nullptr){if(pA == pB) return pA;if(pA == nullptr){pA = headB;}else{pA = pA->next;}if(pB == nullptr){pB = headA;}else{pB = pB->next;}}return nullptr;}};
LeetCode 141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
思路:快慢指针,快指针一次走两步,慢指针一次走一步,如果没环,快指针会先走到链表尾,如果有环,快指针会先入环,而后慢指针入环,因为二者步幅差1,所以最终一定会相遇。
我的解法:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/class Solution {public:bool hasCycle(ListNode *head) {if(!head || !head->next) return false; //如果头节点和头节点的下一个是空,那么肯定不会成环ListNode* fast = head->next;ListNode* slow = head;while(fast){if(fast == slow){return true;}if(fast->next){fast = fast->next->next;;}else{ return false; }slow = slow->next;}return false;}};
LeetCode 138. 复制带随机指针的链表
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
-
val:一个表示Node.val的整数。 -
random_index:随机指针指向的节点索引(范围从0到n-1);如果不指向任何节点,则为null。
你的代码 只 接受原链表的头节点 head 作为传入参数。
思路1:
本题要求我们对一个特殊的链表进行深拷贝。如果是普通链表,我们可以直接按照遍历的顺序创建链表节点。而本题中因为随机指针的存在,当我们拷贝节点时,「当前节点的随机指针指向的节点」可能还没创建,因此我们需要变换思路。一个可行方案是,我们利用回溯的方式,让每个节点的拷贝操作相互独立。对于当前节点,我们首先要进行拷贝,然后我们进行「当前节点的后继节点」和「当前节点的随机指针指向的节点」拷贝,拷贝完成后将创建的新节点的指针返回,即可完成当前节点的两指针的赋值。
具体地,我们用哈希表记录每一个节点对应新节点的创建情况。遍历该链表的过程中,我们检查「当前节点的后继节点」和「当前节点的随机指针指向的节点」的创建情况。如果这两个节点中的任何一个节点的新节点没有被创建,我们都立刻递归地进行创建。当我们拷贝完成,回溯到当前层时,我们即可完成当前节点的指针赋值。注意一个节点可能被多个其他节点指向,因此我们可能递归地多次尝试拷贝某个节点,为了防止重复拷贝,我们需要首先检查当前节点是否被拷贝过,如果已经拷贝过,我们可以直接从哈希表中取出拷贝后的节点的指针并返回即可。
在实际代码中,我们需要特别判断给定节点为空节点的情况。
复杂度分析
时间复杂度:O(n),其中 n 是链表的长度。对于每个节点,我们至多访问其「后继节点」和「随机指针指向的节点」各一次,均摊每个点至多被访问两次。
空间复杂度:O(n),其中 n 是链表的长度。为哈希表的空间开销。
/*// Definition for a Node.class Node {public:int val;Node* next;Node* random;Node(int _val) {val = _val;next = NULL;random = NULL;}};*/class Solution {public:unordered_map<Node*, Node*> cacheNode;Node* copyRandomList(Node* head) {if(head == nullptr){return nullptr;} if(!cacheNode.count(head)){Node* headNew = new Node(head->val);cacheNode[head] = headNew;headNew->next = copyRandomList(head->next);headNew->random = copyRandomList(head->random);}return cacheNode[head];}};
我的解法2:
注意到方法一需要使用哈希表记录每一个节点对应新节点的创建情况,而我们可以使用一个小技巧来省去哈希表的空间。
我们首先将该链表中每一个节点拆分为两个相连的节点,例如对于链表 A→B→C,我们可以将其拆分为 A→A′→B→B′→C→C′ 。对于任意一个原节点 S,其拷贝节点 S′ 即为其后继节点。
这样,我们可以直接找到每一个拷贝节点 S′ 的随机指针应当指向的节点,即为其原节点 SSS 的随机指针指向的节点 T 的后继节点 T‘ 。需要注意原节点的随机指针可能为空,我们需要特别判断这种情况。
当我们完成了拷贝节点的随机指针的赋值,我们只需要将这个链表按照原节点与拷贝节点的种类进行拆分即可,只需要遍历一次。同样需要注意最后一个拷贝节点的后继节点为空,我们需要特别判断这种情况。
复杂度分析
时间复杂度:O(n),其中 n 是链表的长度。我们只需要遍历该链表三次。读者们也可以自行尝试在计算拷贝节点的随机指针的同时计算其后继指针,这样只需要遍历两次。 空间复杂度:O(1)。注意返回值不计入空间复杂度。
/*// Definition for a Node.class Node {public:int val;Node* next;Node* random;Node(int _val) {val = _val;next = NULL;random = NULL;}};*/class Solution {public:Node* copyRandomList(Node* head) {if(head == nullptr){return nullptr; //如果为空则不讨论}for(Node* node = head; node != nullptr; node = node->next->next){Node* newNode = new Node(node->val);nodeNew->next = node->next;node->next = nodeNew; //创建新节点在原节点之后}for(Node* node = head; node != nullptr; node = node->next->next){Node* nodeNew = node->next;newNode->random = (node->random != nullptr) ? node->random : nullptr;//修改新链表random的指向}Node* headNew = head->next;for(Node* node = head; node != nullptr; node = node->next){Node* nodeNew = node->next; node->next = node->next->next; //修改原链表的next。nodeNew->next = (nodeNew->next != nullptr) ? nodeNew->next->next : nullptr; //修改新链表的next指向}return headNew;}};