LWE和RLWE问题学习

LWE概念

又称误差还原，容错学习问题，即已知一个矩阵 $A$ 以及一个向量，求解
$\hat{b}=A x+e$
这里 $e$ 是一个固定数值范围内随机采集的一个随机噪音向量，所以这个问题就转化为通过 $A$ 和 $\hat{b}$ 来还原最初的未知向量 $x$
可以理解为：需要找到一组系数，使得一组基向量的线性组合无线逼近目标向量，使用噪音误差的大小来定义我们需要距离目标向量有多近。

分类
一般分为两类，决策LWE（简称为DLWE）的设定和搜索LWE（简称为SLWE）基本相同。唯一不同的是，SLWE最后的问题是需要我们找到 $s$ ，而DLWE只需要让我们辨别看到的 $\hat b = As+e$ 到底是LWE问题中的误差乘积还是一个随机生成的向量。

LWE分类

搜索LWE问题（Search LWE Problem）

关键概念
在这里插入图片描述
$LWE\left(n, m, q, x_{B}\right): Search Version\\ Let A \stackrel{R}{\leftarrow} \mathbb{Z}_{q}^{m \times n}, s \stackrel{R}{\leftarrow} \mathbb{Z}_{q}^n, e \stackrel{R}{\leftarrow} x_{B} \\ Given (A, A s+e) , find s^{\prime} \in \mathbb{Z}_{q}^{n} s.t. \left\|A s^{\prime}-(A s+e)\right\|_{\infty} \leq B$
帮助理解：
这里开始定义了四个重要的参数，

$m$ 代表线性方程组有多少个方程，
$n$ 代表了每个方程中有多少个未知数。
$q$ 则是有限域的大小，一般来说这会是一个足够大的素数。
误差噪音取值上限 $B$ 的大小决定问题中需要找到的解距离实际取值 $\hat{b}$ 可以相差多少。
$R$ 代表随机选取。

结合各个参数的含义，则LWE问题的定义就是给定矩阵 $A$ 与误差乘积 $A s + e$ ，如何能够搜索出（search）一个合理的 $As^{\prime}$ ，使得得到的向量和问题给定的 $A s + e$ 之间的误差不能超过误差上限 $B$ 。

可以理解为：给定矩阵 $A$ 以及带有误差的结果 $A s + e$ 还原出未知的向量 $s$ 。

来看看这些个参数会如何影响LWE问题的难度

如果系统中的未知变量越多那么，问题将越难，也就是增大 $n$ 的大小会增加LWE问题的难度， $n$ 也被称为LWE问题的安全参数。
$m$ 可以看作 $n$ 的多项式倍数，如果可用的方程组越多，那么解出未知向量就会容易一些。
$q$ 也可以看作 $n$ 的多项式倍数
误差 $B$ 需要比 $q$ 小很多，这样找到正确的解老说会相对简单。

决策LWE问题（Decisional LWE Problem）

在解决证明一个困难问题的安全性的时候，我们一般都会使用决策版本的LWE问题（Decisional LWE）

$E\left(n, m, q, x_{B}\right) : Decisional Version\\ \operatorname{Let} A \stackrel{R}{\leftarrow} \mathbb{Z}_{q}^{m \times n}, s \stackrel{R}{\longleftarrow} \mathbb{Z}_{q}^n, e \stackrel{R}{\leftarrow} x_{B}, v \stackrel{R}{\longleftarrow} \mathbb{Z}_{q}^{m} .\\ Distinguish (A, A s+e) from (A, v) .$
只能看到两个值， $A$ 和 $\hat b$ ，需要辨别出看到的到底是一个LWE问题实例 $\hat b = As+e$ ，还是一个随机变量 $v$
由于LWE问题本身就是困难的，所以从 $A s + e$ 中提取出未知变量 $x$ 来是很困难的，也就是，在我们眼中 $A s + e$ 和一个随机变量其实没多大区别，没法获取有价值的信息。
一般来说参数一个个生成比较费力，所以一般都指定一个参数例如 $n$ 然后交给一个函数 $f (n)$ 来生成其他参数的输出，只要保证参数生成符合要求即可。

LWE算法

LWE私钥加密算法

LWE加密的本质思想是，把消息明文 $m$ (0或1)叠加到随机均匀的LWE实例 $< a, s > + e$ 上，就像one-time-pad一样，叠加后的结果与随机均匀选取的数区分不出来。

由于 $\in \mathbb{Z_q}$ ，因此它的值在 $(- q /2, q /2]$ 之间。
注意，这里的模运算是取的中心模。一般的模运算采用的是向下取整，也就是 $\mod p = a- \lfloor a/p \rfloor * p$ 。故模 $p$ 的通常范围是 $[0, p - 1]$ ，而中心模使用的是 $\mod p = a- \lceil a/p \rfloor * p$ ，使用的最近整数。顾故，模p的范围是 $(- p /2, p /2]$ 。可以把中心模看作是将 $(p /2, p]$ 映射到 $(- p /2, 0]$ 上面。

然后将 $(- q /2, q /2]$ 看作一个有限环域，当需要加密一个bit的时候，把这个bit映射到环上去，0代表环的一头（即0），1代表环的另一头（即q/2），这就相当于对消息进行编码。我们叠加的噪音就等于是把这个映射的点往上或者往下位移了一部分，这样只要噪音的大小不过分（低于q/4），我们就可以通过看这个值到底在环的哪一侧来判断这个bit的具体取值了。但是一旦叠加噪音超过了临界值，那么就无法判断bit的值了。假如，噪音变大了，就有可能导致误差上限超过临界值，一旦超过，那么0和1极有可能映射到相同的点上去，那就导致解密失败。
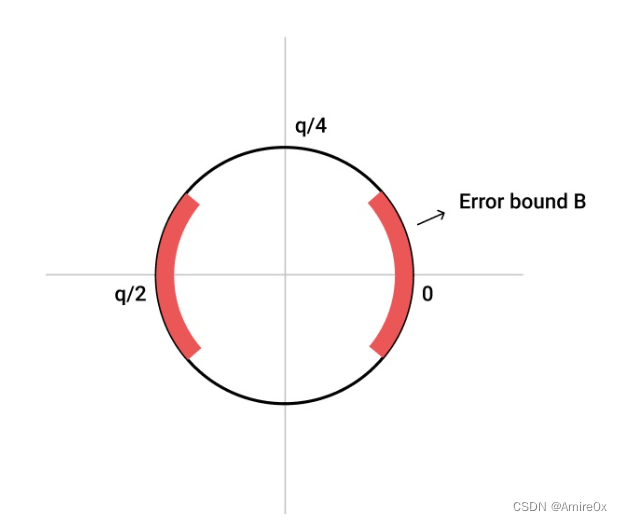
在这里插入图片描述
当然，消息也可以是一个有限数值，如 $\in \mathbb{Z_t}$ ，同样可以把消息空间映射到有限环域 $Z_q$ 上。思路如下，

这里的 $m + e$ ，由于带有噪声叠加，所以是没法直接解密的，也不能像比特加密一样单纯的映射到两个点周围。那么这里的加密就需要把 $m$ 搬到 $\mathbb{Z_q}$ 的高位上，相当于把 $m$ 放大了 $q / t$ 倍，即，把长度为 $t$ 的从地位端挪到了模 $q$ 的高位端。这样噪声因为比较小就会留在低位，这样明文和噪声分离，就容易解出明文。
在这里插入图片描述
由此，私钥加密算法如下，
私钥： $\leftarrow \mathbb{Z_q^n}$
消息： $\leftarrow \mathbb{Z_t^m}$
LWE参数： $\leftarrow \mathbb{Z_q^{m \times n}}$ 和向量 $\leftarrow \chi^m$ ，计算 $\mod q$
加密： $(A,c=\lfloor q/t \rfloor \cdot m +b )$
解密： $\lfloor \dfrac{t}{q}(c-As) \mod q \rceil \mod t$
令 $\lfloor q/t \rfloor= q/t - \triangle$ ，其中 $0\le \triangle <1$ ，解密时， $\dfrac{t}{q}m+(e-\triangle m)$ ，当噪声 $(e-\triangle m)$ 小于 $q /2 t$ 时，就近取整好就能正确还原 $m$ 。当 $t = 2$ 的时候就是对比特加密。

帮助理解：把 $t$ 这么长的消息空间，映射到 $q$ 这么长的环上去，等价于把 $q$ 直接 $t$ 等分，每一份代表一个值，（例如 $t = 2$ 就是把 $q$ 一分为二， $t = 4$ 就是把q一分为四），此时要想解密不出错，那么肯定要 $m + e$ 这个值在一份 $q / t$ 里面，这样才能正确解密，因为有个就近取整的四舍五入操作，所以 $e$ 不能大于一份 $q / t$ 的一半，即 $e < (q / t) /2$ 。

Regev的LWE公钥加密算法

这是一个基于DLWE（决策性LWE问题）的格密码学中的公钥加密系统，对比特加密
具体内容
在这里插入图片描述

正确性验证
将解密部分计算展开
$\begin{array}{c} \tilde{x}=c_{1}-c_{0} \cdot s \\ =r^{T} b+q / 2 \cdot x-r^{T} A s \\ =r^{T}(A s+e)-r^{T} A s+q / 2 \cdot x \\ =r^{T} e+q / 2 \cdot x \end{array}$
在这里插入图片描述

RLWE概念

环LWE问题是LWE问题在环上的版本，不同的是 $A$ 和 $s$ 的选取是在多项式环上。
多项式环 $R_q= \mathbb{Z_q}[x]/f(x)$ ，表示每次计算后都要对多项式系数模 $q$ ，对多项式模 $f (x)$ 。它其中的每个元素都是一个多项式，每一次操作都相当于对多个元素进行操作，也就是能够一次加密多个比特的明文，对比LWE每次仅能对一个比特操作来说能够大大提高效率满足实际需要。

RLWE分类

同样，它也有两个版本，即search 和 decision。
先定义一些参数，安全参数 $n$ ，模 $q(n)\ge 2$ ， $f(x) = x^d +1$ 其中 $d = d (n)$ 是2的幂次， $\mathbb{Z}[x]/f(x)$ ， $R_q = \mathbb{Z}_q[x]/f(x)$ ， $\chi$ 是 $R$ 上的错误概率分布。
随机选取 $\leftarrow R_q$ ， $a_i \leftarrow R_q$ ，噪声 $e_i \leftarrow \chi$ ，令 $b_i = a_i \cdot s +e_i$ ，其中 $i=1,\ldots,m$

搜索性RLWE

简述就是，给定 $m$ 个 $a_i,b_i)$ ，求解出秘密元素 $\leftarrow R_q$ 。

判定性RLWE

区分 $m$ 个随机均匀选取自 $R_q \times R_q$ 的 $a_i,b_i)$ 和m个 $(a_i,b_i = a_i \cdot s+e_i)$ ，其中 $a_i \leftarrow R_q$ ，噪声 $e_i \leftarrow \chi$ 。

RLWE算法

RLWE公钥加密算法

$SecretKeyGen(1_{\lambda})$ :随机均匀选取 $\leftarrow R_q$ 。

$P u b l i cKey G e n (s k)$ :随即均匀选取 $\leftarrow R_q$ ，噪声 $e_1 \leftarrow \chi$ ，计算 $\cdot s +e_1$ ， $\in R_q \times R_q$ 。

$E n c (p k, m)$ :加密 $n$ 位消息 $\in \{0,1\}^n$ ，把它看作多项式 $\in R_2$ 的系数。随机选择 $e_2,e_3,e_4 \leftarrow \chi$ ，输出密文 $c_1,c_2)$ 。其中
$c_1= \lfloor q/2 \rfloor \cdot m+be_2+e_3 \in R_q \\ c_2=ae_2+e_4 \in R_q$

$Dec (c, s k)$ :计算
$\lfloor \frac{2}{q}[(c_1-c_2\cdot s)\mod q] \rceil \mod 2 \lfloor \frac{2}{q}[<c,s>] \mod q \rceil \mod 2$
解密的正确性
$\begin{aligned} c_1-c_2s &= \lfloor q/2 \rfloor \cdot m+be_2+e_3-(ae_2s+e_4s) \\ &=\lfloor q/2 \rfloor \cdot m+e_1e_2+e_3-e_4s \end{aligned}$
可以看到噪声 $e^* = e_1e_2+e_3-e_4s$ ，当噪声小于 $\lfloor q/2 \rfloor/2$ 时，解密正确

RLWE公钥加密算法变形

噪声是偶数的形式，可以通过模2直接消除。
$SecretKeyGen(1_{\lambda})$ :随机均匀选取 $\leftarrow R_q$ 。

$P u b l i cKey G e n (s k)$ :随即均匀选取 $a_1 \leftarrow R_q$ ，噪声 $e_1 \leftarrow \chi$ ，计算 $\cdot s +2e_1$ ， $\in R_q \times R_q$ 。

$E n c (p k, m)$ :加密 $n$ 位消息 $\in \{0,1\}^n$ ，把它看作多项式 $\in R_2$ 的系数。随机选择 $e_2,e_3,e_4 \leftarrow \chi$ ，输出密文 $c_1,c_2)$ 。其中
$c_1= m+be_2+2e_3 \in R_q \\ c_2=ae_2+2e_4 \in R_q$

$Dec (c, s k)$ :计算
$=[(c_1-c_2\cdot s)\mod q] \mod 2$
解密的正确性
$\begin{aligned} c_1-c_2s &= m+be_2+2e_3-(ae_2s+2e_4s) \\ &=m+2e_1e_2+2e_3-2e_4s \end{aligned}$
可以看到噪声 $e^* = 2e_1e_2+2e_3-2e_4s$ ，模2的时候噪声就可以直接消除。