一、卷积神经网络基本概念

卷积神经网络包含了一个由卷积层和子采样层构成的特征抽取器。在卷积神经网络的卷积层中，一个神经元只与部分邻层神经元相连接。在CNN的一个卷积层中，通常包含若干个特征平面，每个特征平面都由一些矩形排列的神经元组成，同一特征平面的神经元共享权重参数，这里共享的权重参数就是卷积核。
卷积核一般由随机小数矩阵的形式初始化，随着神经网络的不断训练，卷积核将会学习到更合理的权值。共享权值（卷积核）可以减少网络各层之间的连接，同时降低过拟合的风险。
子采样也叫做池化（pooling），通常有均值子采样（mean pooling）和最大值子采样（max pooling）两种形式。子采样可以看作一个特殊的卷积过程。卷积和子采样可以简化模型的复杂度，减少模型的参数。

二、卷积神经网络原理

2.1神经网络

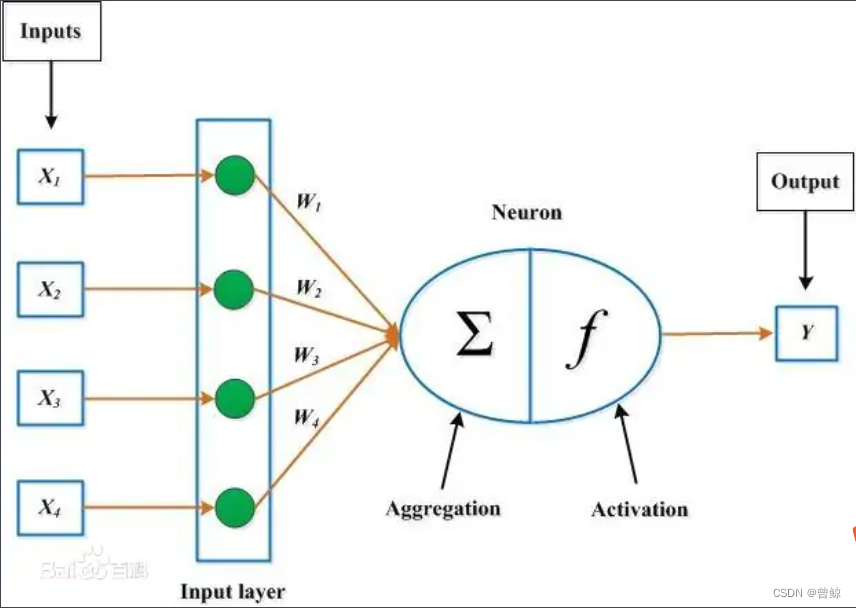
神经网络的每个单元如下：
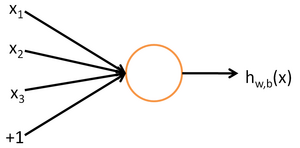
在这里插入图片描述
其对应的公式为：

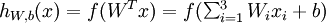
该单元也可以被称作Logistic回归模型。当多个单元组合起来并具有分层结构时，就形成了神经网络模型。下图是一个具有隐含层的神经网络：

其对应的公式为：

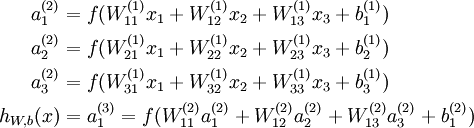
同时，我们可以拓展到有2，3，4，5，…个隐含层。
神经网络的训练方法也与Logistic类似，可以利用梯度下降+链式求导法则，又称反向传播算法。

2.2卷积神经网络

卷积神经网络由三部分组成：输入层、由n个卷积层和池化层的组合组成、全连结的多层感知机分类器。
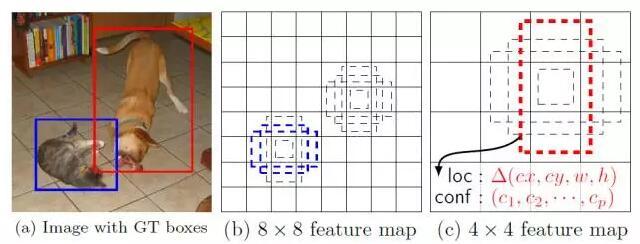
2.2.1局部感受野
卷积神经网络通过局部感受野来降低参数数目。在图像中，距离较远的像素相关性较弱，因此每个神经元没必要对全局图像进行感知，只需要对局部进行感知，然后在更高层将局部信息综合起来，得到全局信息。
假设每个神经元只与1010的像素值相连，那么权值数据就为1000000100个参数，减少为原来的万分之一。1010的像素值对应的1010个参数就相当于卷积操作。
2.2.2权值共享
使用了局部感受野后参数仍然过多，那么就要使用权值共享。在上面的局部连接中，每个神经元都对应100个参数，如果所有神经元对应的参数都是相等的，那么参数数目就是100。
我们将这100个参数看作特征提取的方式，这个方式与位置无关。因此，图像的一部分统计特性和其他部分是一样的，所以我们在这一部分上学习的特征，也可以应用在其他部分。
比如，我们在一个大尺寸图像中，随机选择一小块，比如44作为样本，我们从小样本中学习到了一些特征，我们就可以把这些特征作为探测器，应用到全部的图像中。特别的，我们可以把这个样本中学习到的特征与原本的大尺寸图像作卷积，从而对这个大尺寸图像上的任意位置获得一个不同特征的激活值。
2.2.3多卷积核
在上面的叙述中，我们知道，如果有100个参数，则表示有一个1010的卷积核，这样做的特征提取是不充分的，我们可以添加多个卷积核，比如32个卷积核，那就可以学习32个特征。如果我们对四个通道进行卷积操作，有两个卷积核，会生成两个通道。需要注意的是，四个通道上每个通道都对应一个卷积核，如果将w2忽略，只看w1，那么在w1的某位置（i,j）处的值，是由四个通道上（i.j）处的卷积结果相加，再取激活函数的值得到的。
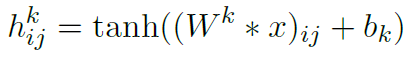
在这里插入图片描述

在上图的4个通道卷积得到2个通道的过程中，参数数目为4222个，其中4是4个通道，第一个2表示生成2个通道，最后的22是卷积核的大小。
2.2.4Down-pooling
在卷积得到了特征后，我们可以用这些特征去做分类。如果我们用所有提取到的特征去训练分类器，如softmax分类器，就会面临很大的计算量。比如，对于一个9696像素的图像，假设我们已经学习得到了400个定义在88输入上的特征，每一个特征和图像卷积都会得到一个（96-8+1）（96-8+1）=7921维的卷积特征，由因为有400个特征，所以每个样例都会有7921400=3168400维的卷积特征向量。所以学习一个拥有三百万特征的输入分类器非常不容易，容易出现过拟合。
因此，为了描述比较大的图像，我们可以对不同位置的特征进行聚合统计，比如，我们可以计算图像一个区域上的某个特定特征的平均值（或最大值）。这些概要统计特征不仅具有低得多的维度（不需使用所有提取到的特征），同时还会改善结果。这种聚合操作就叫做池化，按照池化的方法可以分为平均池化和最大池化。
在这里插入图片描述
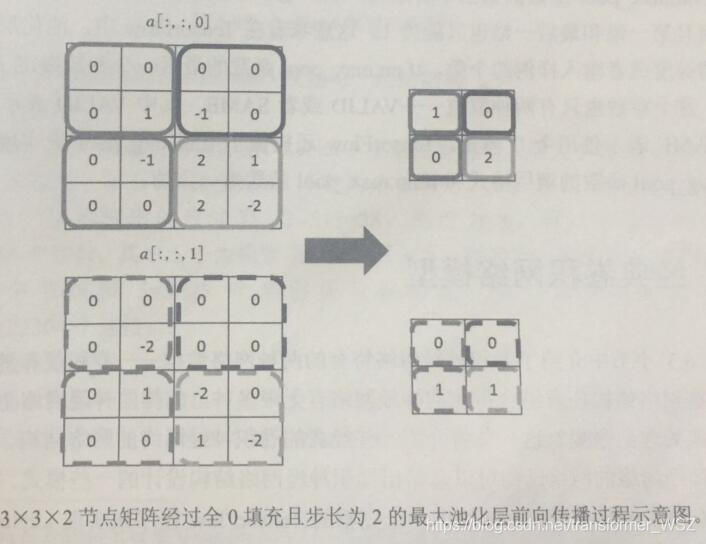
如上图：
1.最大值子采样卷积核中，只有一个权重值为1，其余为0；值为1的位置对应的inputX被卷积核覆盖部分值最大的位置。图示的卷积核滑动步长为2.最大子采样效果是把原图缩减至原来的1/4，并保留每个2*2区域的最大输入。
2.均值子采样的卷积核中，每个权重都是相同的。上图的均值子采样是把原图模糊缩减至原来的1/4。
2.2.5多卷积层
实际应用中，一般使用多层卷积，然后用全连接层训练，一层卷积学到的特征一般是局部的，层数越高，学到的特征越全局化。