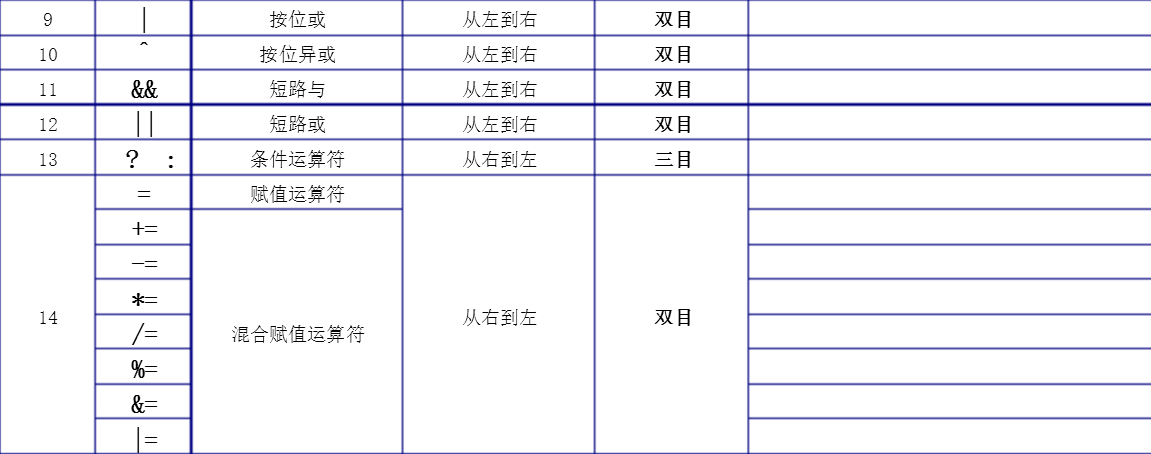
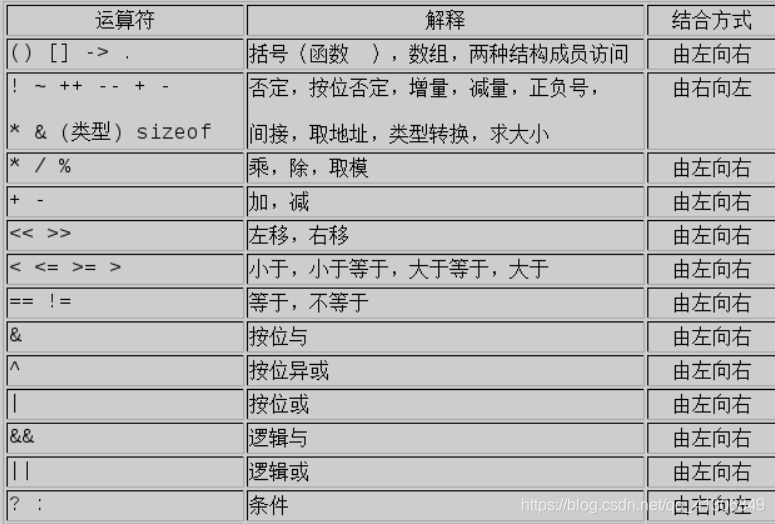
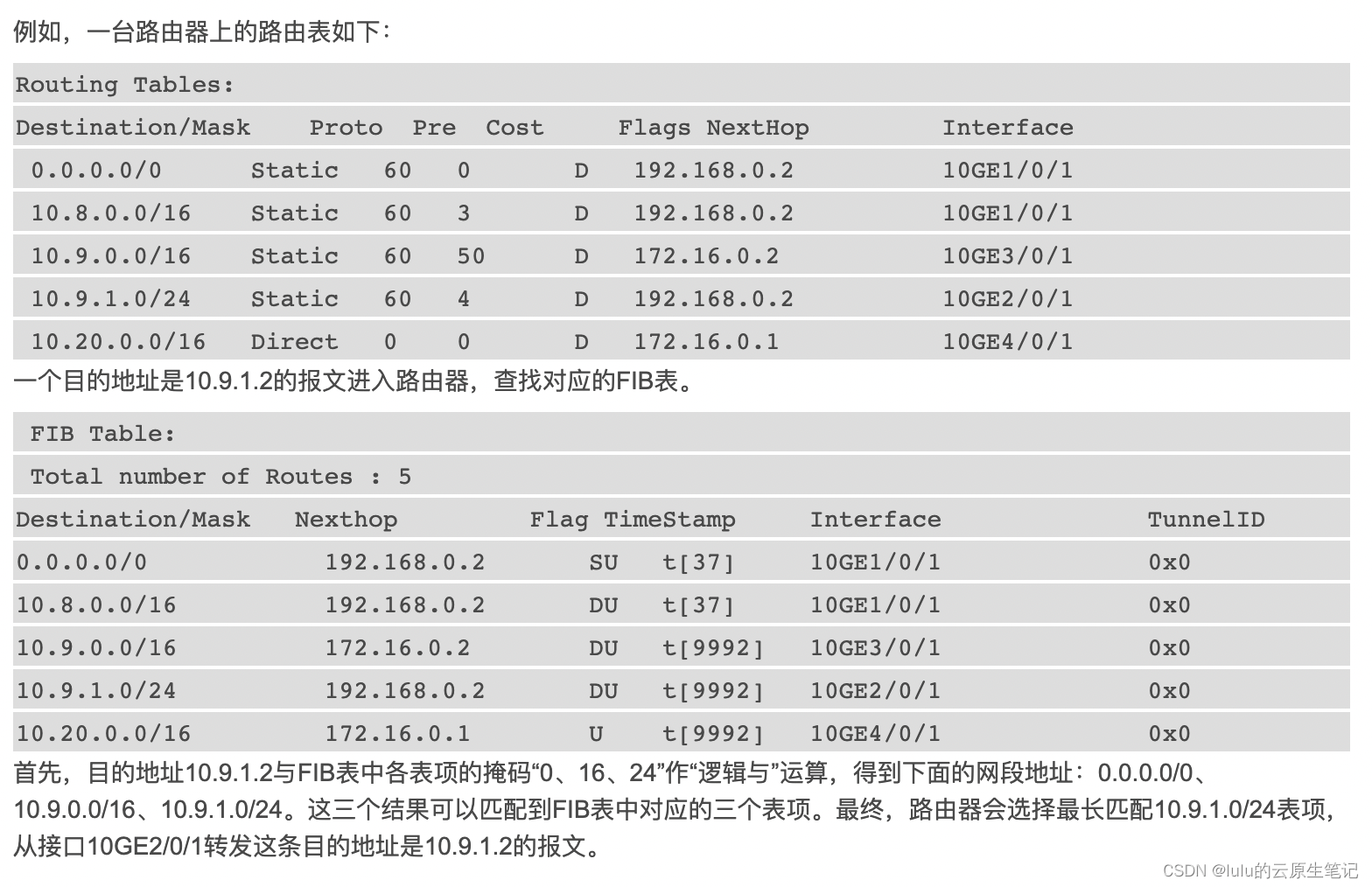
摘自:http://www.cnblogs.com/luluping/archive/2010/03/03/1677552.html
浅析求素数算法
注意: 如果没有特殊说明, 以下讨论的都是针对n为素数时的时间复杂度
1. 根据概念判断:
如果一个正整数只有两个因子, 1和p,则称p为素数.
bool isPrime(int n)
{if(n < 2) return false;for(int i = 2; i < n; ++i)if(n%i == 0) return false;return true;
} 时间复杂度O(n).
2. 改进, 去掉偶数的判断
bool isPrime(int n)
{if(n < 2) return false;if(n == 2) return true;if(n%2==0) return false;for(int i = 3; i < n; i += 2)if(n%i == 0) return false;return true;
} 时间复杂度O(n/2), 速度提高一倍.
3. 进一步减少判断的范围
定理: 如果n不是素数, 则n有满足1<d<=sqrt(n)的一个因子d.
证明: 如果n不是素数, 则由定义n有一个因子d满足1<d<n.
如果d大于sqrt(n), 则n/d是满足1<n/d<=sqrt(n)的一个因子.
bool isPrime(int n)
{if(n < 2) return false;if(n == 2) return true;for(int i = 3; i*i <= n; i += 2)if(n%i == 0) return false;return true;
} 时间复杂度O(sqrt(n)/2), 速度提高O((n-sqrt(n))/2).
4. 剔除因子中的重复判断.
例如: 11%3 != 0 可以确定 11%(3*i) != 0.
定理: 如果n不是素数, 则n有满足1<d<=sqrt(n)的一个"素数"因子d.
证明: I1. 如果n不是素数, 则n有满足1<d<=sqrt(n)的一个因子d.
I2. 如果d是素数, 则定理得证, 算法终止.
I3. 令n=d, 并转到步骤I1.
由于不可能无限分解n的因子, 因此上述证明的算法最终会停止.
// primes[i]是递增的素数序列: 2, 3, 5, 7, ...
// 更准确地说primes[i]序列包含1->sqrt(n)范围内的所有素数bool isPrime(int primes[], int n)
{if(n < 2) return false;for(int i = 0; primes[i]*primes[i] <= n; ++i)if(n%primes[i] == 0) return false;return true;
}
假设n范围内的素数个数为PI(n), 则时间复杂度O(PI(sqrt(n))).
函数PI(x)满足素数定理: ln(x)-3/2 < x/PI(x) < ln(x)-1/2, 当x >= 67时.
因此O(PI(sqrt(n)))可以表示为O(sqrt(x)/(ln(sqrt(x))-3/2)),
O(sqrt(x)/(ln(sqrt(x))-3/2))也是这个算法的空间复杂度.
5. 构造素数序列primes[i]: 2, 3, 5, 7, ...
由4的算法我们知道, 在素数序列已经被构造的情况下, 判断n是否为素数效率很高;
但是, 在构造素数序列本身的时候, 是否也可是达到最好的效率呢?
事实上这是可以的! -- 我们在构造的时候完全可以利用已经被构造的素数序列!
假设我们已经我素数序列: p1, p2, .. pn
现在要判断pn+1是否是素数, 则需要(1, sqrt(pn+1)]范围内的所有素数序列,
而这个素数序列显然已经作为p1, p2, .. pn的一个子集被包含了!
// 构造素数序列primes[]void makePrimes(int primes[], int num)
{int i, j, cnt;primes[0] = 2;primes[1] = 3;for(i = 5, cnt = 2; cnt < num; i += 2){int flag = true;for(j = 1; primes[j]*primes[j] <= i; ++j){if(i%primes[j] == 0){flag = false; break;}}if(flag) primes[cnt++] = i;}
}
makePrimes的时间复杂度比较复杂, 而且它只有在初始化的时候才被调用一次.
在一定的应用范围内, 我们可以把近似认为makePrimes需要常数时间.
在后面的讨论中, 我们将探讨一种对计算机而言更好的makePrimes方法.
6. 更好地利用计算机资源...
当前的主流PC中, 一个整数的大小为2^32. 如果需要判断2^32大小的数是否为素数,
则可能需要测试[2, 2^16]范围内的所有素数(2^16 == sqrt(2^32)).
由4中提到的素数定理我们可以大概确定[2, 2^16]范围内的素数个数.
由于2^16/(ln(2^16)-1/2) = 6138, 2^16/(ln(2^16)-3/2) = 6834,
我们可以大概估计出[2, 2^16]范围内的素数个数6138 < PI(2^16) < 6834.
在对[2, 2^16]范围内的素数进行统计, 发现只有6542个素数:
p_6542: 65521, 65521^2 = 4293001441 < 2^32, (2^32 = 4294967296)
p_6543: 65537, 65537^2 = 4295098369 > 2^32, (2^32 = 4294967296)
在实际运算时unsigned long x = 4295098369;将发生溢出, 为131073.
在程序中, 我是采用double类型计算得到的结果.
分析到这里我们可以看到, 我们只需要缓冲6543个素数, 我们就可以采用4中的算法
高效率地判断[2, 2^32]如此庞大范围内的素数!
(原本的2^32大小的问题规模现在已经被减小到6543规模了!)
虽然用现在的计算机处理[2, 2^16]范围内的6542个素数已经没有一点问题,
虽然makePrimes只要被运行一次就可以, 但是我们还是考虑一下是否被改进的可能?!
我想学过java的人肯定想把makePrimes作为一个静态的初始化实现, 在C++中也可以
模拟java中静态的初始化的类似实现:
#define NELEMS(x) ((sizeof(x)) / (sizeof((x)[0])))
static int primes[6542+1];
static struct _Init { _Init(){makePrimes(primes, NELEMS(primes);} } _init;
如此, 就可以在程序启动的时候自动掉用makePrimes初始化素数序列.
但, 我现在的想法是: 为什么我们不能在编译的时候调用makePrimes函数呢?
完全可以!!! 代码如下:
// 这段代码可以由程序直接生成const static int primes[] =
{
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,
107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,
223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,
337,347,349,353,359,367,373,379,383,389,397,401,409,419,421,431,433,439,443,449,
457,461,463,467,479,487,491,499,503,509,521,523,541,547,557,563,569,571,577,587,
593,599,601,607,613,617,619,631,641,643,647,653,659,661,673,677,683,691,701,709,
719,727,733,739,743,751,757,761,769,773,787,797,809,811,821,823,827,829,839,853,
857,859,863,877,881,883,887,907,911,919,929,937,941,947,953,967,971,977,983,991,
...
65521, 65537
};
有点不可思议吧 , 原本makePrimes需要花费的时间复杂度现在真的变成O(1)了!
, 原本makePrimes需要花费的时间复杂度现在真的变成O(1)了!
(我觉得叫O(0)可能更合适!)
7. 二分法查找
现在我们缓存了前大约sqrt(2^32)/(ln(sqrt(2^32)-3/2))个素数列表, 在判断2^32级别的
素数时最多也只需要PI(sqrt(2^32))次判断(准确值是6543次), 但是否还有其他的方式判断呢?
当素数比较小的时候(不大于2^16), 是否可以直接从缓存的素数列表中直接查询得到呢?
答案是肯定的! 由于primes是一个有序的数列, 因此我们当素数小于2^16时, 我们可以直接
采用二分法从primes中查询得到(如果查询失败则不是素数).
// 缺少的代码请参考前边#include <stdlib.h>static bool cmp(const int *p, const int *q)
{return (*p) - (*q);
}bool isPrime(int n)
{if(n < 2) return false;if(n == 2) return true;if(n%2 == 0) return false;if(n >= 67 && n <= primes[NELEMS(primes)-1]){return NULL !=bsearch(&n, primes, NELEMS(primes), sizeof(n), cmp);}else{for(int i = 1; primes[i]*primes[i] <= n; ++i)if(n%primes[i] == 0) return false;return true;}
} 时间复杂度:
if(n <= primes[NELEMS(primes)-1] && n >= 67): O(log2(NELEMS(primes))) < 13;
if(n > primes[NELEMS(primes)-1]): O(PI(sqrt(n))) <= NELEMS(primes).
8. 素数定理+2分法查找
在7中, 我们对小等于primes[NELEMS(primes)-1]的数采用2分法查找进行判断.
我们之前针对2^32缓冲的6453个素数需要判断的次数为13次(log2(1024*8) == 13).
对于小的素数而言(其实就是2^16范围只内的数), 13次的比较已经完全可以接受了.
不过根据素数定理: ln(x)-3/2 < x/PI(x) < ln(x)-1/2, 当x >= 67时, 我们依然
可以进一步缩小小于2^32情况的查找范围(现在是0到NELEMS(primes)-1范围查找).
我们需要解决问题是(n <= primes[NELEMS(primes)-1):
如果n为素数, 那么它在素数序列可能出现的范围在哪?
---- (n/(ln(n)-1/2), n/(ln(n)-3/2)), 即素数定理!
上面的代码修改如下:
bool isPrime(int n)
{if(n < 2) return false;if(n == 2) return true;if(n%2 == 0) return false;int hi = (int)ceil(n/(ln(n)-3/2));if(n >= 67 && hi < NELEMS(primes)){int lo = (int)floor(n/(ln(n)-1/2));return NULL !=bsearch(&n, primes+lo, hi-lo, sizeof(n), cmp);}else{for(int i = 1; primes[i]*primes[i] <= n; ++i)if(n%primes[i] == 0) return false;return true;}
}
时间复杂度:
if(n <= primes[NELEMS(primes)-1] && n >= 67): O(log2(hi-lo))) < ???;
if(n > primes[NELEMS(primes)-1]): O(PI(sqrt(n))) <= NELEMS(primes).
9. 打包成素数库(给出全部的代码)
到目前为止, 我已经给出了我所知道所有改进的方法(如果有人有更好的算法感谢告诉我).
这里需要强调的一点是, 这里讨论的素数求法是针对0-2^32范围的数而言, 至于像寻找
成百上千位大小的数不在此讨论范围, 那应该算是纯数学的内容了.
代码保存在2个文件: prime.h, prime.cpp.
到这里, 关于素数的讨论基本告一段落. 回顾我们之前的求解过程, 我们会发现
如果缺少数学的基本知识会很难设计好的算法; 但是如果一味地只考虑数学原理,
而忽律了计算机的本质特征, 也会有同样的问题.
一个很常见的例子就是求Fibonacci数列. 当然方法很多, 但是在目前的计算机中
都没有实现的必要!
因为Fibonacci数列本身是指数增长的, 32位的有符号整数所能表示的位置只有前46个:
1 // file: prime.h2 3 #ifndef PRIME_H_2006_10_27_4 #define PRIME_H_2006_10_27_5 6 extern int Prime_max(void); // 素数序列的大小7 extern int Prime_get (int i); // 返回第i个素数, 0 <= i < Prime_max8 9 extern bool Prime_test(int n); // 测试是否是素数, 1 <= n < INT_MAX10 11 #endif12 13 ///14 15 // file: prime.cpp16 17 #include <assert.h>18 #include <limits.h>19 #include <math.h>20 #include <stdlib.h>21 22 #include "prime.h"23 24 // 计算数组的元素个数25 26 #define NELEMS(x) ((sizeof(x)) / (sizeof((x)[0])))27 28 // 素数序列, 至少保存前6543个素数!29 30 static const int primes[] = 31 {32 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,33 107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,34 223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,313,317,331,35 337,347,349,353,359,367,373,379,383,389,397,401,409,419,421,431,433,439,443,449,36 457,461,463,467,479,487,491,499,503,509,521,523,541,547,557,563,569,571,577,587,37 593,599,601,607,613,617,619,631,641,643,647,653,659,661,673,677,683,691,701,709,38 719,727,733,739,743,751,757,761,769,773,787,797,809,811,821,823,827,829,839,853,39 857,859,863,877,881,883,887,907,911,919,929,937,941,947,953,967,971,977,983,991,40 ...41 65521, 6553742 };43 44 // bsearch的比较函数45 46 static int cmp(const void *p, const void *q)47 {48 return (*(int*)p) - (*(int*)q);49 }50 51 // 缓冲的素数个数52 53 int Prime_max()54 {55 return NELEMS(primes);56 }57 58 // 返回第i个素数59 60 int Prime_get(int i)61 {62 assert(i >= 0 && i < NELEMS(primes));63 return primes[i];64 }65 66 // 测试n是否是素数67 68 bool Prime_test(int n)69 {70 assert(n > 0);71 72 if(n < 2) return false;73 if(n == 2) return true;74 if(!(n&1)) return false;75 76 // 如果n为素数, 则在序列hi位置之前77 78 int lo, hi = (int)ceil(n/(log(n)-3/2.0));79 80 if(hi < NELEMS(primes))81 {82 // 确定2分法查找的范围83 // 只有n >= 67是才满足素数定理84 85 if(n >= 67) lo = (int)floor(n/(log(n)-1/2.0));86 else { lo = 0; hi = 19; }87 88 // 查找成功则为素数89 90 return NULL !=91 bsearch(&n, primes+lo, hi-lo, sizeof(n), cmp);92 }93 else94 {95 // 不在保存的素数序列范围之内的情况96 97 for(int i = 1; primes[i]*primes[i] <= n; ++i)98 if(n%primes[i] == 0) return false;99
100 return true;
101 }
102 }