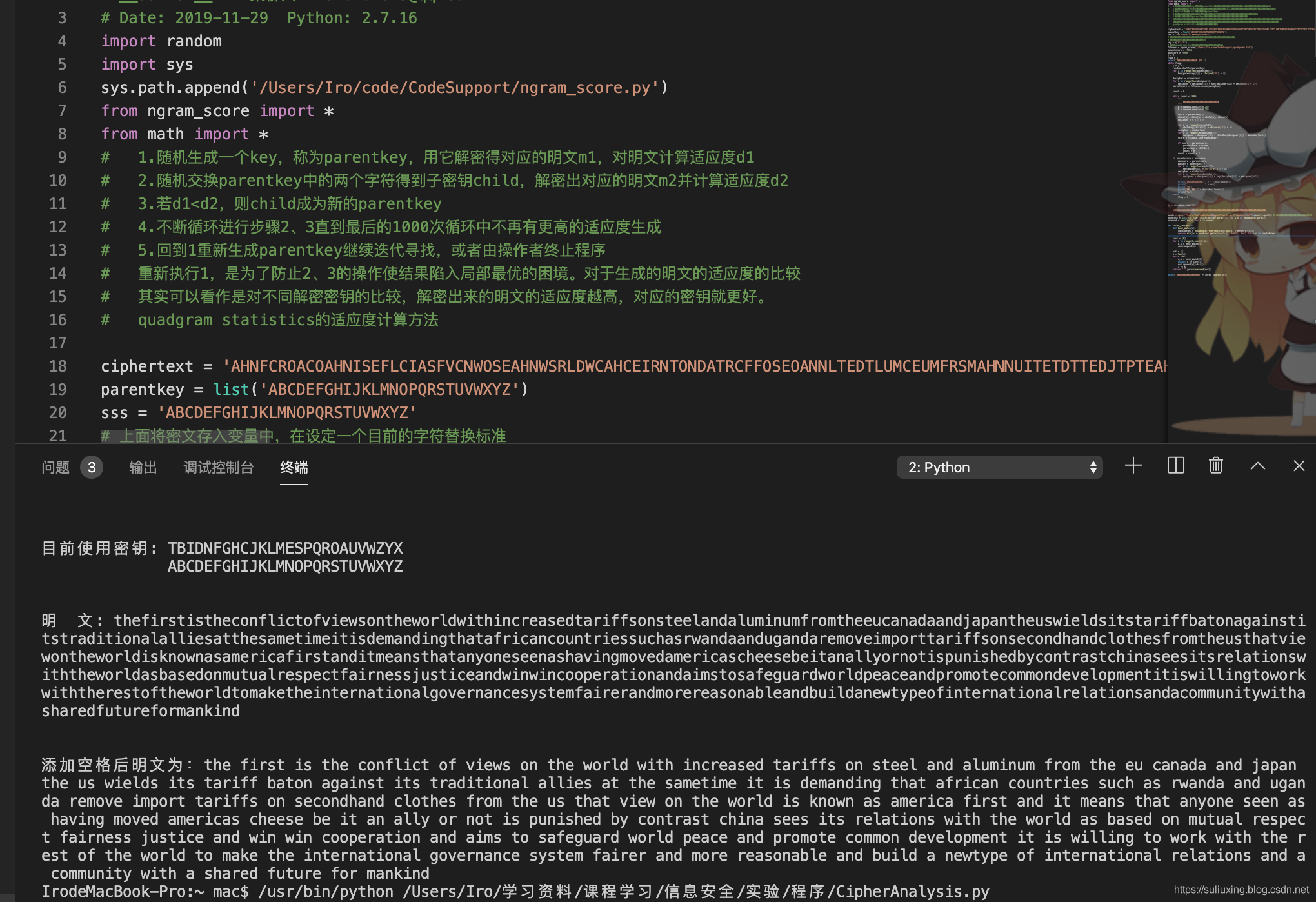
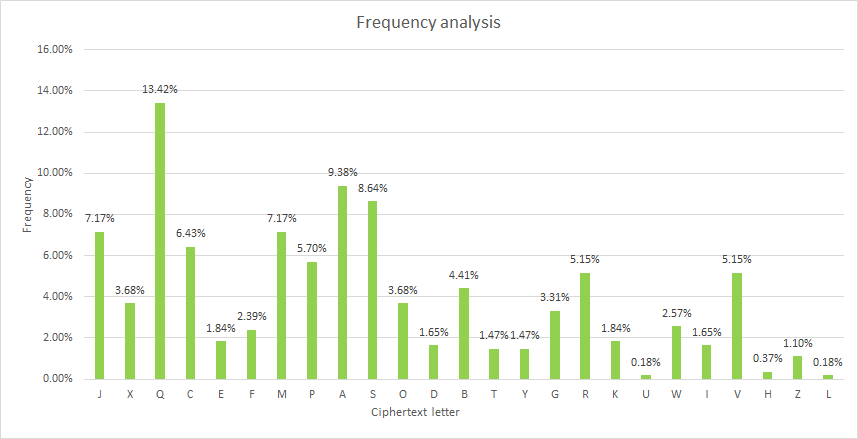
差分密码分析是针对SPN结构中的S盒(通过测试可以探测出结构)进行分析的方法,最后目标是破解出异或密钥k.

准备工作

对于一个4位一组的S盒的输入$x$输出$y$输入$x^{\ast }$输出$y^{\ast }$,
计差分为$x^{\prime }=x\oplus x^{\ast }$,$y^{\prime }=y\oplus y^{\ast }$.
则4位下$x^{\prime }$和$y^{\prime }$各有$2^4$种.差分分析就基于$x\oplus x^{\ast }$相等的明文对的集合对应的密文对$y\oplus y^{\ast }$在$2^4$下的不均匀分布有关.
定义$\Delta (x^{\prime })$为包含所有异或为$x^{\prime }$的明文对的集合.y亦然.
在本篇文章种如果没有特殊说明,明文指S盒加密前的比特,密文指加密后的.

主要流程

确定$x^{\prime }$
计算该集合下的每一对的$y^{\prime }$
定义$N_D(x^{\prime },y^{\prime })$为明文异或为x’.密文异或为y’的对数.
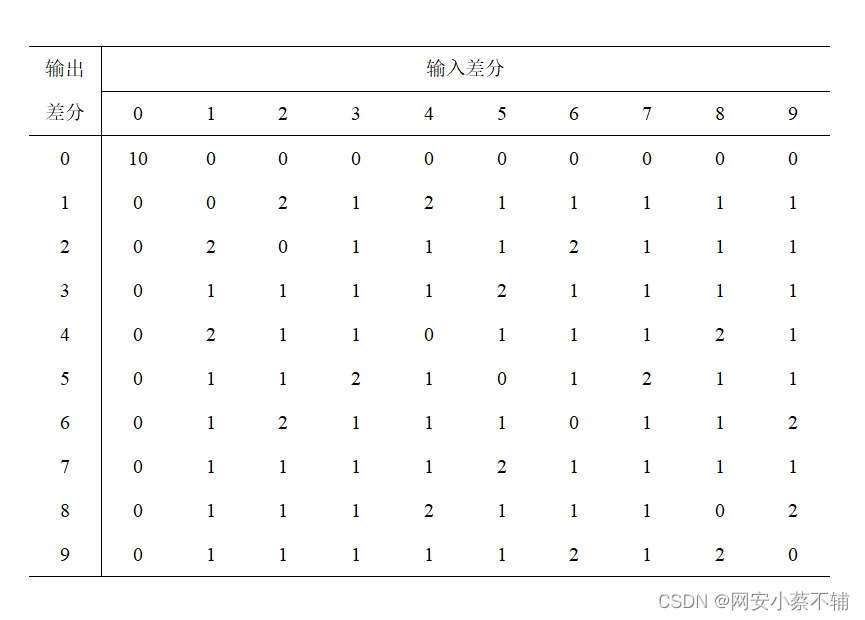
计算每一个可能的x’的情况,打表如下

a’为明文的异或,b’为密文的异或.

注意到,对于SPN的加密规则,下一轮S的输入等于上一轮P盒的输出异或子密钥.
则$x\oplus x^{\ast }=w\oplus w^{\ast }$,因为作为同一位置上的输入,密钥被抵消.

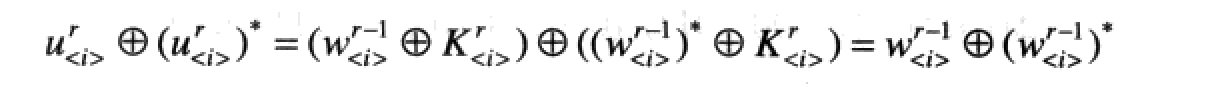
但y’仍然和密钥有关.
定义扩散率为x’=a下y’=b的概率.即
$$R_p(a^{\prime },b^{\prime })=\frac{N_D(a^{\prime },b^{\prime })}{2^m}$$
和线性分析一样,要找到一个差分链使得下一轮的差分输入异或是上一轮的输出异或置换之后的结果,这样就能得到整个差分链的扩散率.
注意:这要求了明文的差分应该是固定的.这一条链中x’应该是0000 1011 0000 0000.

实现

差分分析和线性分析类似,当输出的异或满足差分链要求时counter+1,然后筛选出最大的.
比如上面的差分链,简单的代码思路如下:

generate_plain_chiper_pairs(T);
if pairs is Correct:
for each possible key:generate v_4_2generate v_4_4generate u_4_2generate u_4_4#v is output,u is input.4_2 means 4th rounds and 2nd part.'''part2'''generate v*_4_2generate v*_4_4generate u*_4_2generate u*_4_4calculate u'_4_2calculate u'_4_4if u'_4_2 is 0110 and u'_4_4 is 0110:counter+1
Select the max

Correct

也就是为了排除噪音的干扰并加强效率,一个可用的明文对应该满足
$$(u_{<1>}^4{)}^{\prime }=(u_{<3>}^4{)}^{\prime }=0$$
即
$$\begin{gathered} y_{<1>}=y_{<1>}^{\ast } \\ {y}_{<3>}=y_{<3>}^{\ast } \end{gathered}$$
否则就要丢弃.

T

一般取T=50-100.