一、 算法原理
1. 概念引入
生成与特征多项式

2. BM算法流程

二、 编程思路
1. 编程思路:
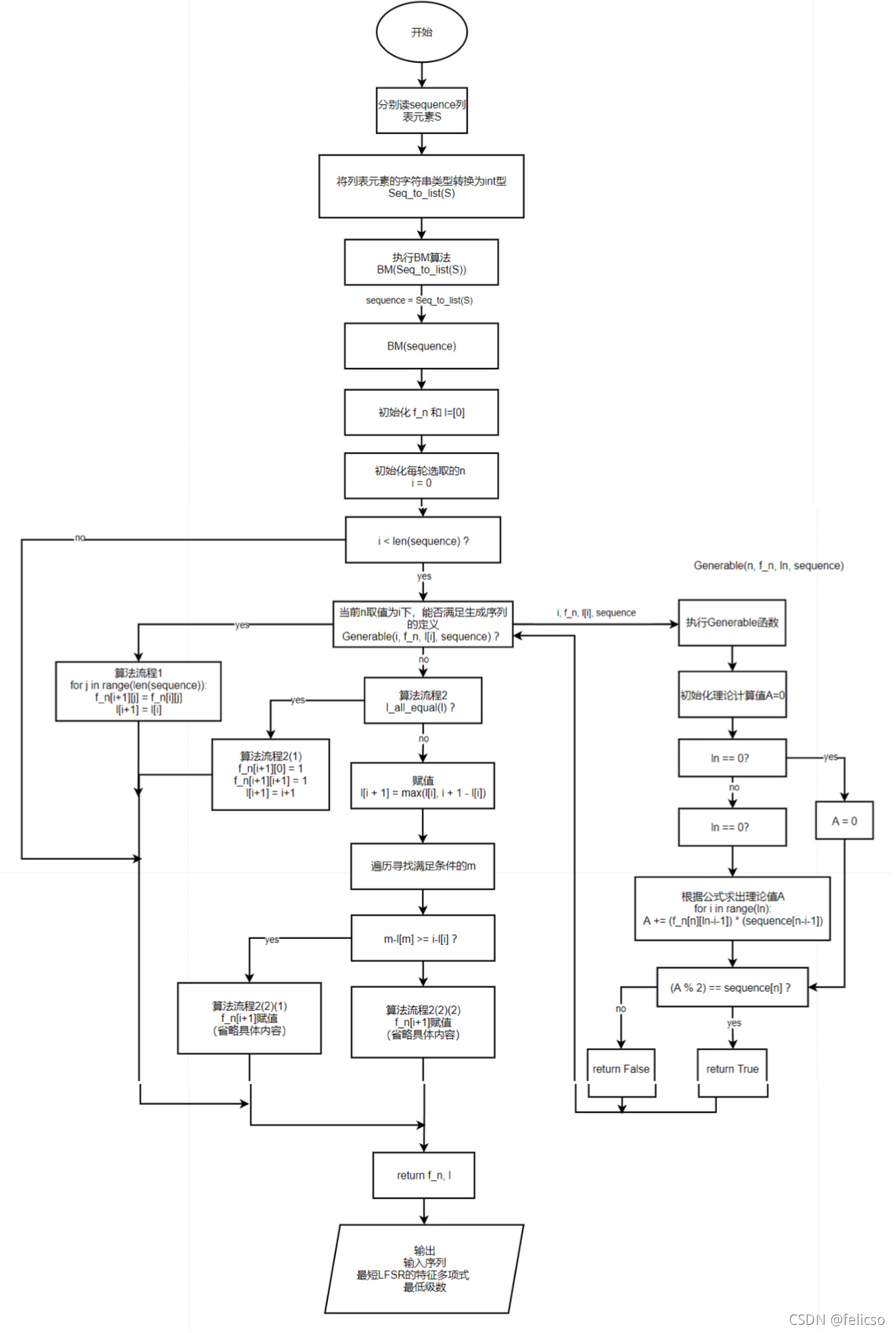
BM算法整体流程较为清晰,其中包含几个核心判断:fnx 能否生成序列a的前n+1位,各l值是否全相等,以及当l值出现不等情况下m-lm和n-ln的相对大小关系;编程分别通过Generable(n, f_n, ln, sequence)函数,l_all_equal(l)函数,以及循环遍历找m然后比较m-lm和n-ln大小关系的方式实现。
编程时在确定f_n (x)时表示形式上有纠结,开始想的是用一个一维数组保存当前轮f_n (x)各项系数,后发现在算法流程2(2)中会用到之前轮的f_m (x),最终采用二维数组来表示f_n (x),其中第一维表示不同轮,第二维表示该轮下各项系数。
x的幂和fnx 相乘相当于fnx对应多项式系数列表右移了x的幂次数位,在做多项式相加运算时用到的即多项式系数列表下标减去相应幂次数(注意下标越界问题)
因为是在二元域下的运算,还要给相应系数进行模2运算。
2. 关键函数:Generable(n, f_n, ln, sequence):
传入参数:当前轮下n的取值,存放每轮最低次多项式的二维数组f_n,当前轮的次数ln,序列sequence
实现代码如下:

3. 算法流程图:
三、 结果截图
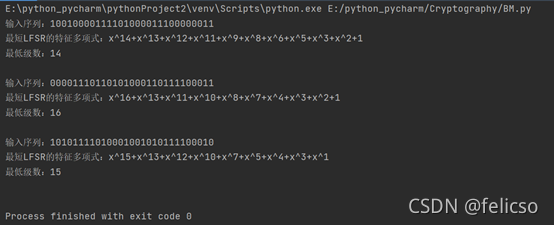
四、 代码
# 判断f_n[n]是否可以生成a的第n+1项
def Generable(n, f_n, ln, sequence):A = 0 # 理论计算值if ln == 0:A = 0else:for i in range(ln): # Ci = f_n[n][l[n]-i-1]A += (f_n[n][ln-i-1]) * (sequence[n-i-1])if (A % 2) == sequence[n]:# print(n, "okkkkkk", ln, f_n[n])return Trueelse:# print(n, "noooooo", ln, f_n[n])return False# BM算法
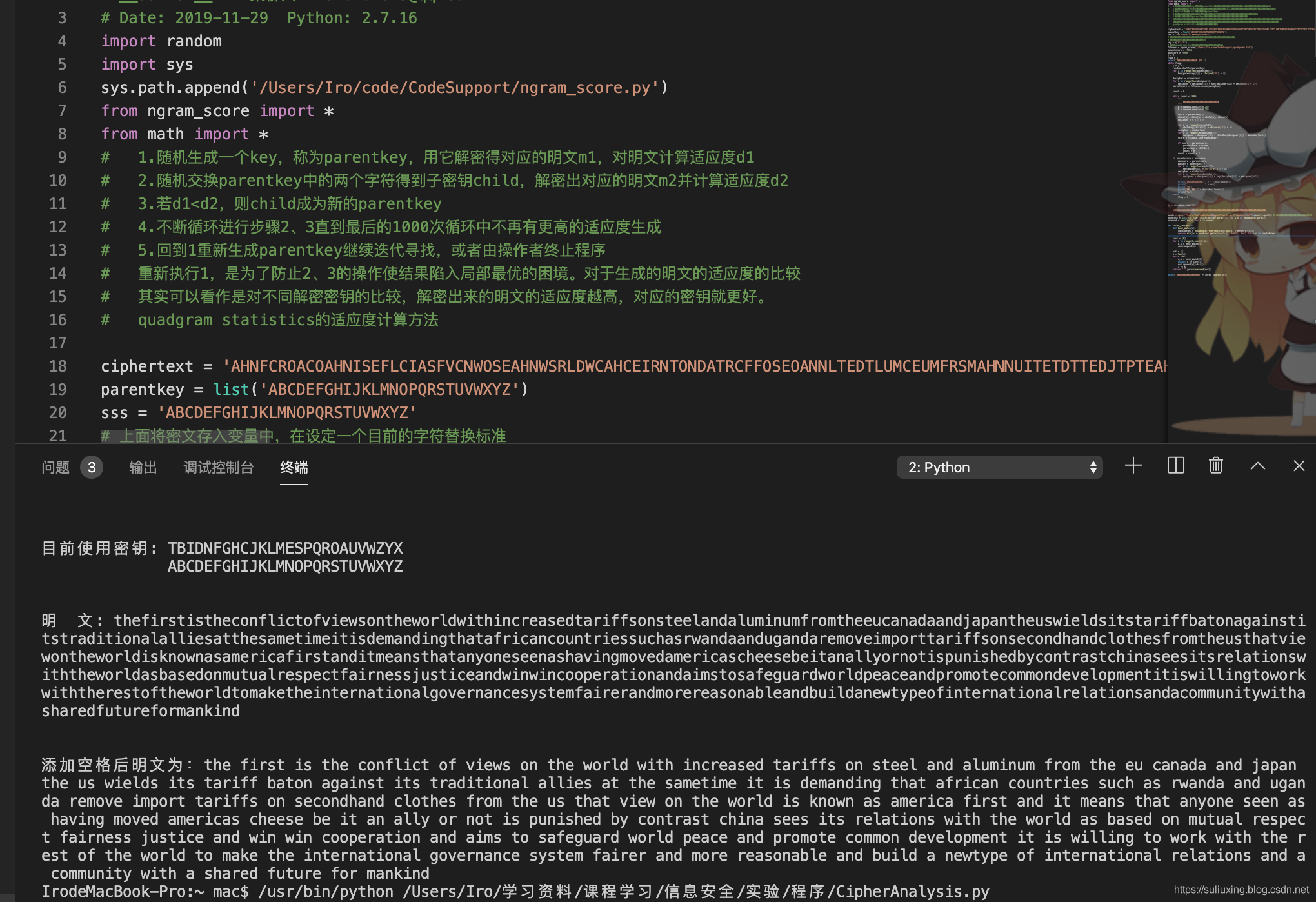
def BM(sequence):f_n = [[0 for i in range(len(sequence))] for i in range(len(sequence)+1)]f_n[0][0] = 1 # 赋初值 f0=1l = [0 for i in range(len(sequence)+1)] # 记录每一轮最低次多项式次数for i in range(len(sequence)):if Generable(i, f_n, l[i], sequence): # 算法流程 1for j in range(len(sequence)):f_n[i+1][j] = f_n[i][j]l[i+1] = l[i]continueelse: # 算法流程 2if l_all_equal(l): # 2(1)# print("execute 2(1)")f_n[i+1][0] = 1f_n[i+1][i+1] = 1l[i+1] = i+1else: # 2(2)j = il[i + 1] = max(l[i], i + 1 - l[i])while j <= i:# print(i, j, l[i], l[j])if l[j] < l[i]:m = jbreakj -= 1if(m-l[m] >= i-l[i]): # 2(2)(1)# print("execute 2(2)(1)")for k in range(i-l[i]-m+l[m]+1):f_n[i+1][k] = (f_n[i][k]) % 2for k in range(i-l[i]-m+l[m], l[i+1]+1):f_n[i+1][k] = (f_n[i][k] + f_n[m][k-(m-l[m]-i+l[i])]) % 2else: # 2(2)(2)# print("execute 2(2)(2)")for k in range(i-l[i]-m+l[m]+1):f_n[i+1][k] = (f_n[m][k]) % 2for k in range(i-l[i]-m+l[m], l[i+1]+1):f_n[i+1][k] = (f_n[i][k-(i-l[i]-m+l[m])] + f_n[m][k]) % 2return f_n, l# 判断l列表中的数字是否全部相同
def l_all_equal(l):for i in range(len(l) - 1):if l[i] != l[i + 1]:return Falsereturn True# 还原多项式字符串并返回
def print_f(f_n, i):result = ''j = l[i]while j >= 0 :if f_n[i][j] != 0:if j == 0:result += '1 +'else:result += 'x^' + str(j) + '+'j -= 1return result[0:-1]# 将字符串转为int形列表
def Seq_to_list(sequence):result = []for i in sequence:result.append(int(i))return resultif __name__ == "__main__":seq = ['10010000111101000011100000011', '00001110110101000110111100011', '10101111010001001010111100010']for S in seq:f_n, l = BM(Seq_to_list(S))print('输入序列:' + S)print('最短LFSR的特征多项式:' + print_f(f_n, len(S)))print('最低级数:' + str(l[len(S)]))print(" ")