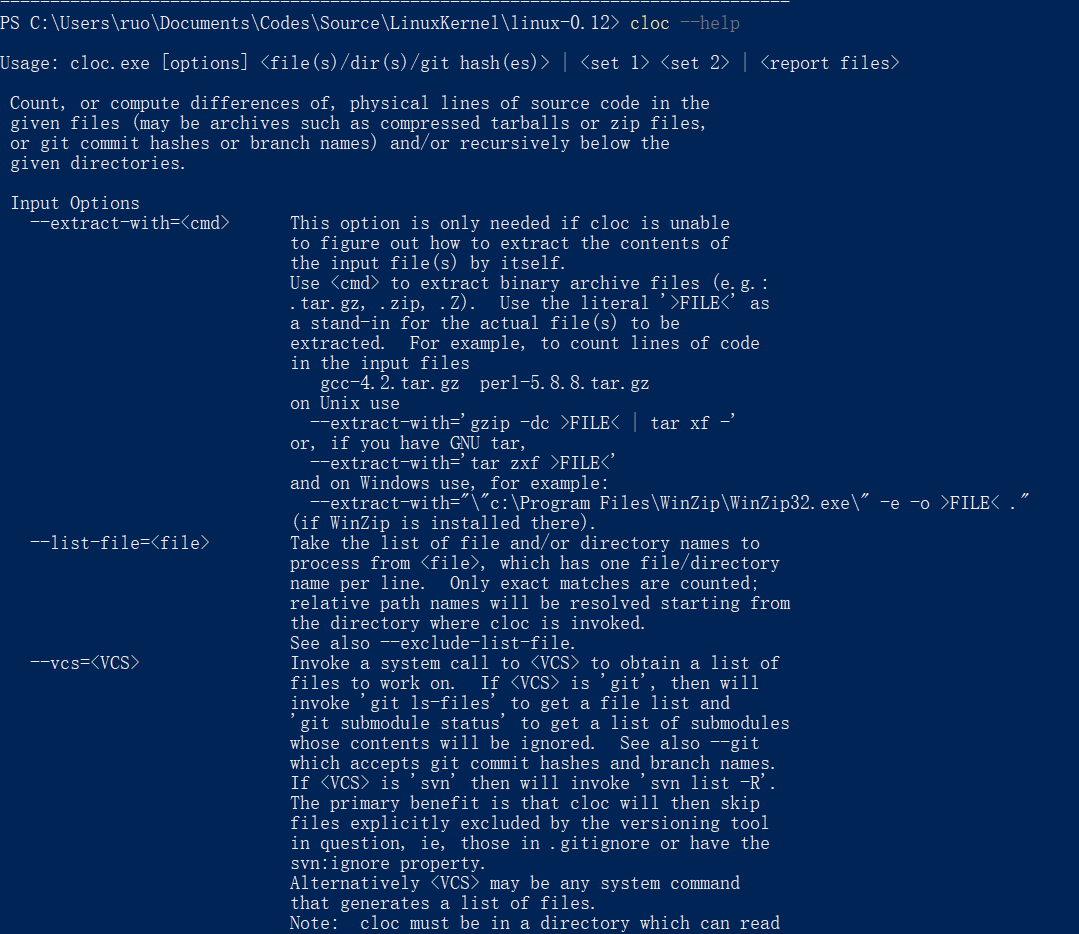
简单迷宫问题

- 一、问题描述
- 二、数据组织
- 三、算法说明
- 附录：完整代码

#简单迷宫问题

一、问题描述

给定一个M×N得迷宫，求一条从指定入口到出口得迷宫路径。假设一个迷宫如图1所示，（这里M=N=8)，其中每个方块用空白表示通道，用阴影表示障碍物。
在这里插入图片描述

规定和要求：

所求得迷宫路径是简单路径，即在求得得迷宫路径上不重复出现同一方块。
迷宫可能有多个路径，这里只考虑求得其中一条。

二、数据组织

为了表示迷宫，一般会很自然得考虑使用一个二维数组表示，如使用 $m g [M] [N]$ ，其中每个元素使用0表示可通行单元，使用1表示障碍物。

但是在本解法中，采用栈数数据结构存储所有的障碍物得坐标，使用一个整形数字（4个字节）表示。具体来说就是使用一个整形的高位2个字节表示坐标的X，使用整形的低2个字节表示坐标Y。因此使用一个整形数字就能完成上图中障碍物的坐标表示。由于考虑的问题规模较小，所以2个字节能表示的迷宫大小足够我们使用了。

对坐标的存储及其操作

/* 分别取出2个整形的高2位和低2位，合并为1个整形，这里假设hi，low小于65535 */
int _maze_element_maker(int hi,int low){return (hi << (sizeof(int)*8/2)) | low ;
}

在迷宫中，位置的移动是体现在坐标的变化，为了描述方便，我们使用地图方向描述，比如向坐标轴X正方向移动，就是向东EAST移动，因此对坐标四个方向的移动，可以使用以下的函数实现。


int _maze_step_north(int e){return e - (1 << sizeof(int) * 4);
}int _maze_step_south(int e){return e + (1 << sizeof(int) * 4);
}int _maze_step_west(int e){return e - 1;
}int _maze_step_east(int e){return e + 1;
}

数据栈的实现

本案例取自《数据结构》教材第3章栈，因此这里使用的栈，是使用C语言实现了的栈的数据结构。因此完整的代码中包含顺序栈的实现。为了方便介绍，这先给出栈的数据结构，以及主要函数的声明。

顺序栈的定义

typedef int ElemType,*ElemTypePtr;
typedef struct{int stack_size;ElemType *top,*bottom;
} Stack;

定义了栈中存储的数据类型是ElemType，对应的指针类型是ElemTypePtr（等效 ElemType *）。从以上代码的第1行定义可以知道，实际代码ElemType类型就是int。所以后面所有的代码中，ElemType就是int类型。

基本栈的操作函数


/* 定义栈中元素遍历时候的处理函数指针类型 */
typedef int (*TranversAtom)(ElemType);/* 遍历栈元素操作*/
int Traverse(Stack* stack,TranversAtom transAtom);/* 初始化栈 */
int InitStack(Stack* stack);/* 获得栈中元素个数 */
long StackLength(Stack* stack);/* 释放栈 */
void DestroyStack(Stack* stack);/* 获得栈顶元素 */
ElemType GetTop(Stack *stack);/* POP操作 */
ElemType Pop(Stack *stack);/* PUSH操作*/
void Push(Stack* stack, ElemType elem);

以上的是使用C语言实现的顺序栈的函数声明，具体代码实现可以参考附录中完整代码，这里不再叙述，这里特别注意Traverse函数是用于遍历栈中的所有元素的函数，在后面的算法中，可以实现检查将要入栈的元素是否已经在栈中操作，而不需要将整个栈中元素都POP出来。

三、算法说明

1.算法

本算法的采用双栈进行求解，一个工作栈和一个路径栈配合工作。工作栈用于记录下一步可能走的所有位置，用于不断的试探，而路径栈就存放如果试探到下一步可以走，那么将其位置放入路径栈中。而如果试探向后没有任何路可走，那么弹出工作栈顶的试探元素，实现后退到上一步的分析，然后再从工作栈顶找到其他的可能的点进行分析。直到工作栈顶分析的元素和终点相等，表明已经走到了终点，此时算法结束。

注意：

工作栈存放的是下一步可能走的位置点，所以栈顶总是准备尝试的位置。
路径栈是已经走过的点，栈顶是最近走到的位置。
当遇无路可走的时候，说明工作栈顶这个点是死路，所以出栈，准备尝试其他方向。
当连续退回多个步的时候，不但工作栈中尝试的点要出栈，同时还要在退栈的过程中检测已经走过的路径栈顶是不是同一个点，如果是，那么也需要同步退栈。简单说，就是同时工作栈和路径栈相同的点都要出栈，以保证回退过程数据的一致。
算法假设迷宫总是存在到终点的路线。

2.代码实现

主要算法代码：

Push(&stack_path, 0);  /* 压入0值，用于分割迷宫原始障碍物坐标和求解的路径坐标。 */
Push(&stack_work, start);do{e = GetTop(&stack_work);if (e==GetTop(&stack_path)) { /* 检查将要分析的位置e是否在路径栈中 */Pop(&stack_path);         /* 如果存在，说明这条路前面已经走过，*/Pop(&stack_work);         /* 现在再次出现在工作栈顶端，说明这条*/continue;                 /* 路走不通，所以全部退栈，放弃！！  */}count = 0;next = _maze_step_east(e);if(_maze_position_valid(&stack_path, next)){Push(&stack_work, next);count++;}next = _maze_step_north(e);if(_maze_position_valid(&stack_path, next)){Push(&stack_work, next);count++;}next = _maze_step_west(e);if(_maze_position_valid(&stack_path, next)){Push(&stack_work, next);count++;}next = _maze_step_south(e);if(_maze_position_valid(&stack_path, next)){Push(&stack_work, next);count++;}if(count>0){                  /* count不为零，表明在当前的位置e是有下一步    */Push(&stack_path, e);     /* 可走的，所以将e位置压入路径栈中，假设走一步 */}else if(Pop(&stack_work)==GetTop(&stack_path)) /* e向后无路可走的情况下，工作栈退栈    */Pop(&stack_path);                          /* 同时，如果路线最近走过这个点，也放弃。*/}while(e!=end);

以上代码整体比较简单，比较难以理解的地方已经添加了注释，其思路就是每次从工作栈中出栈的点，如果是回溯情况下，那么必须将路径栈中的点也弹出。

程序运行效果如图2。
在这里插入图片描述

3.算法小结

本算法使用了2个栈保存数据，使用了循环代替了通常使用的DFS算法。因为通常使用DFS算法实现都是使用的函数递归，因此对于数据量很大的情况下，有可能会出现程序栈溢出的情况。但是本算法重新实现了顺序栈，并且顺序栈是可以不断按需要延展的。所以理论上程序规模只会收到主机内存大小的限制。

附录：完整代码

#include <stdio.h>
#include <stdlib.h>#define STACK_INIT_SIZE 100
#define STACK_RELLOC_SIZE 10/* 顺序栈定义声明 */
typedef int ElemType,*ElemTypePtr;
typedef struct{int stack_size;ElemType *top,*bottom;
} Stack;
typedef int (*TranversAtom)(ElemType);
int InitStack(Stack* stack);
long StackLength(Stack* stack);
void DestroyStack(Stack* stack);
ElemType GetTop(Stack *stack);
ElemType Pop(Stack *stack);
void Push(Stack* stack, ElemType elem);
int Traverse(Stack* stack,TranversAtom transAtom);/* 迷宫辅助函数声明 */
int Travers_Find(ElemType tofind);
ElemType _maze_element_maker(int hi,int low);
ElemType _maze_HiDWord(ElemType e);
ElemType _maze_LoDWord(ElemType e);
void _maze_print(ElemType e);
void _maze_init(Stack* stack);
void _maze_print_map(Stack * stack);
int _maze_position_valid(Stack * stack,ElemType e);
ElemType _maze_step_north(ElemType e);
ElemType _maze_step_south(ElemType e);
ElemType _maze_step_west(ElemType e);
ElemType _maze_step_east(ElemType e);ElemType global_elmt;int main(int argc, char* argv[])
{int count;Stack stack_work, stack_path;ElemType start=_maze_element_maker(8, 8), end=_maze_element_maker(1, 1), e, next;InitStack(&stack_work);/* 工作栈，用于存放试探前进过程得位置，方便回溯。*/InitStack(&stack_path);/* 路径栈，记录已经走过得路径。*/_maze_init(&stack_path);Push(&stack_path, 0);  /* 压入0值，用于分割迷宫原始障碍物坐标和求解的路径坐标。 */Push(&stack_work, start);do{e = GetTop(&stack_work);if (e==GetTop(&stack_path)) { /* 检查将要分析的位置e是否在路径栈中 */Pop(&stack_path);         /* 如果存在，说明这条路前面已经走过，*/Pop(&stack_work);         /* 现在再次出现在工作栈顶端，说明这条*/continue;                 /* 路走不通，所以全部退栈，放弃！！  */}count = 0;next = _maze_step_east(e);if(_maze_position_valid(&stack_path, next)){Push(&stack_work, next);count++;}next = _maze_step_north(e);if(_maze_position_valid(&stack_path, next)){Push(&stack_work, next);count++;}next = _maze_step_west(e);if(_maze_position_valid(&stack_path, next)){Push(&stack_work, next);count++;}next = _maze_step_south(e);if(_maze_position_valid(&stack_path, next)){Push(&stack_work, next);count++;}if(count>0){                  /* count不为零，表明在当前的位置e是有下一步    */Push(&stack_path, e);     /* 可走的，所以将e位置压入路径栈中，假设走一步 */}else if(Pop(&stack_work)==GetTop(&stack_path)) /* e向后无路可走的情况下，工作栈退栈    */Pop(&stack_path);                          /* 同时，如果路线最近走过这个点，也放弃。*/}while(e!=end);_maze_print_map(&stack_path);DestroyStack(&stack_work);DestroyStack(&stack_path);return 0;
}int InitStack(Stack* stack){stack->stack_size = STACK_INIT_SIZE;stack->bottom = (ElemTypePtr)malloc(stack->stack_size*sizeof(ElemType));if (!stack->bottom) {printf(">> 内存分配失败 !\n");return -1;}stack->top = stack->bottom;return 1;
}long StackLength(Stack* stack){return stack->top - stack->bottom;
}void DestroyStack(Stack* stack){if (stack->bottom) {free(stack->bottom);}
}ElemType GetTop(Stack *stack){if (StackLength(stack)) {return *(stack->top-1);}printf(">> 空栈无数据！\n");return 0;
}ElemType Pop(Stack *stack){ElemType el = GetTop(stack);if(StackLength(stack)){stack->top--;return el;}return 0;
}void Push(Stack* stack, ElemType elem){long len =StackLength(stack);if ( len >= stack->stack_size ) {ElemTypePtr tmp = (ElemTypePtr)realloc(stack->bottom, (stack->stack_size+=STACK_RELLOC_SIZE)*sizeof(ElemType));if(tmp){stack->bottom = tmp;stack->top = stack->bottom + len;}else{printf(">> 内存分配失败\n");return;}}*(stack->top) = elem;stack->top++;
}int Traverse(Stack* stack,TranversAtom transAtom){long i,len = StackLength(stack);int ret=0;for (i=0; i<len; i++) {if ((ret = transAtom(*(stack->bottom+i)))!=0) {return ret;}}return ret;
}int Travers_Find(ElemType tofind){return tofind==global_elmt ? 1 : 0;
}ElemType _maze_element_maker(int hi,int low){return (hi << (sizeof(ElemType)*4)) | low ;
}ElemType _maze_step_north(ElemType e){return e - (1 << sizeof(ElemType) * 4);
}ElemType _maze_step_south(ElemType e){return e + (1 << sizeof(ElemType) * 4);
}ElemType _maze_step_west(ElemType e){return e - 1;
}ElemType _maze_step_east(ElemType e){return e + 1;
}ElemType _maze_HiDWord(ElemType e){return e >> (sizeof(ElemType)*4);
}ElemType _maze_LoDWord(ElemType e){return e - (_maze_HiDWord(e) << (sizeof(ElemType)*4));
}void _maze_print(ElemType e){ElemType hi,lo;hi = _maze_HiDWord(e);lo = _maze_LoDWord(e);printf("(%d,%d)",hi,lo);
}void _maze_init(Stack* stack){int i;ElemType x[]={1,2,2,2,3,3,3,3,4,4,4,5,6,6,6,7,7,7/*,5*/};ElemType y[]={8,4,6,7,1,2,4,7,4,5,7,3,3,6,7,1,2,7/*,7*/};    for (i=0; i<sizeof(x)/sizeof(int); i++)Push(stack, _maze_element_maker(y[i], x[i]));for (i=0; i<10; i++) {Push(stack, _maze_element_maker(0,i));Push(stack, _maze_element_maker(9,i));Push(stack, _maze_element_maker(i,0));Push(stack, _maze_element_maker(i,9));}}int _maze_position_valid(Stack * stack,ElemType e){global_elmt = e;    return !Traverse(stack, Travers_Find);
}void _maze_print_map(Stack * stack){ElemType e;int map[10][10]={0},i=1,j;int k=0; int z=0;for(k=0; k<10; k++) {for(z=0; z<10; z++) {map[k][z]=' '-'0';}}puts("$ 迷宫的解:");printf("起点=>");while (GetTop(stack)!=0) {e = Pop(stack);_maze_print(e);printf("=>");map[_maze_HiDWord(e)][_maze_LoDWord(e)] = '@' - '0';}puts("终点.\n");while (StackLength(stack)) {e = Pop(stack);map[_maze_HiDWord(e)][_maze_LoDWord(e)] = '#' - '0';}printf("  ");for (i=0; i<10; i++)printf("%2d",i);printf("\n");for (i=0; i<10; i++) {printf("%2d",i);for (j=0; j<10; j++) {printf("%2c",map[i][j]+'0');}printf("\n");}printf("\n图例：\n# —— 迷宫障碍\n@ —— 线路点\n");
}