一、递归算法

1、递归算法思想

递归算法是在程序中不断反复调用（间接或直接地调用）自身，来达到解决问题的算法。

递归是一个方法在其方法体内调用自身方法的调用方式。递归调用分为两种情况：

• 直接递归，即在方法中调用方法本身
• 间接递归，即间接地调用一个方法

在递归中主方法又是被调方法。执行递归将反复调用其自身。每调用一层就进入新的一层。例如：阶乘问题，斐波那契数列求项等。

2、递归如何实现

数论思想：利用数学公式或者定理或者规律求解问题。

递归的关键就是要找出这个递归公式，并找到递归终止条件。

递归操作使用到了 数论&穷举&回溯&分治&递归算法思想。

编写递归方法时：

• 必须使用 if语句强制在未执行递归前返回。
• 必须要设置终止递归的条件。

特点：

递归经常会对某些问题重复调用，导致算法效率不高，时间复杂度和空间复杂度都很高，很容易导致栈溢出异常。

3、递归使用场景

使用递归时，场景必须满足下面条件：

（1）一个问题的解可以分解为几个子问题的解。

（2）这个问题与分解之后的子问题，求解思路完全一样。

（3）问题一定有一个最后确定的答案，即递归的终止条件。

4、递归优化

（1）使用非递归

理论上，所有的递归代码是一定可以转换成非递归的方式，即不使用递归。

（2）使用缓存
我们把子问题的运算结果保存起来，这样就可以减少重复计算次数，从而降低递归的时间复杂度。有点动态规划算法思想的味道。

（3）使用尾递归

5、什么是尾递归

• 百度百科-尾递归：https://baike.baidu.com/item/%E5%B0%BE%E9%80%92%E5%BD%92/554682

1）什么是尾递归

如果一个函数中所有递归形式的调用都出现在函数的末尾，我们称这个递归函数是尾递归。

当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时，这个递归调用就是尾递归。

尾递归函数的特点： 就是在回归过程中不用做任何其他操作，这个特性很重要，因为大多数现代的编译器会利用这种特点自动生成优化的代码。

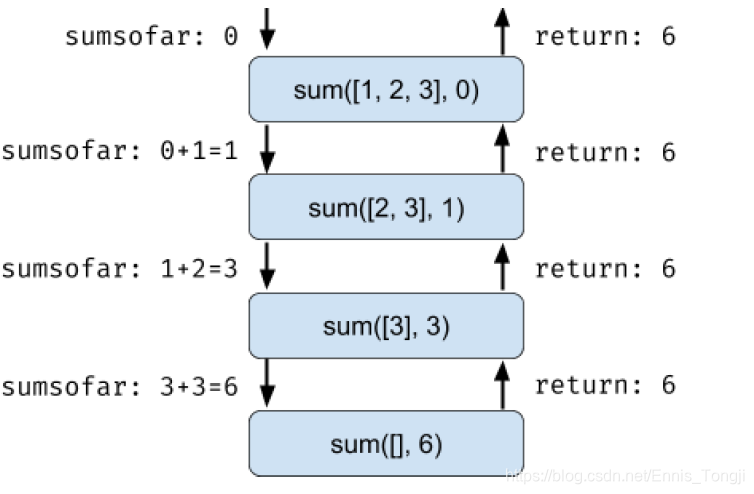
简单理解尾递归： 即就是倒着算，不需要在回溯了，因为我们每次会把中间结果带下去。

因为我们编译器在编译代码时，如果发现函数末尾已经没有操作了，这时候就不会创建新的栈，而且覆盖到前面去。

2）原理
当编译器检测到一个函数调用是尾递归的时候，它就覆盖当前的活动记录而不是在栈中去创建一个新的。编译器可以做到这点，因为递归调用是当前活跃期内最后一条待执行的语句，于是当这个调用返回时栈帧中并没有其他事情可做，因此也就没有保存栈帧的必要了。通过覆盖当前的栈帧而不是在其之上重新添加一个，这样所使用的栈空间就大大缩减了，这使得实际的运行效率会变得更高。

下面对求阶乘问题，斐波那契数列求项使用递归求解。数据越界暂时不考虑。

二、阶乘问题

阶乘（factorial）是基斯顿·卡曼于1808年发明的运算符号。阶乘也是数学里的一种术语，指1乘以2乘以3乘以4持续到所要求的数。比如：n! = 123*…*(n-1)*n

0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120

阶乘递推的方法定义：

f(n) = n * f(n - 1) （n ≥2，n ∈ N*）
f(1) = 1

1、递归求解

	@Testpublic void testFactorial() {//int res = factorial(6);//System.out.println(res);for (int i = 1; i <= 6; i++) {long start = System.currentTimeMillis();System.out.println(i + ":" + factorial(i) + " 所花费的时间为" + (System.currentTimeMillis() - start) + "ms");}}/*** 递归求解：时间复杂度O(2^n)和空间复杂度O(2^n)* @param n* @return*/private static int factorial(int n) {if (n <= 1) {return 1; // 递归的终止条件}return n * factorial(n - 1); // 继续递归的过程}

2、优化递归

（1）使用非递归

	@Testpublic void testNoRecurve() {for (int i = 1; i <= 6; i++) {long start = System.currentTimeMillis();System.out.println(i + ":" + noRecurve(i) + " 所花费的时间为" + (System.currentTimeMillis() - start) + "ms");}}/*** 递归求解优化：使用非递归。时间复杂度O(n)和空间复杂度O(n)* @param n*/private static int noRecurve(int n){if(n <= 1){return 1;}int a = 1;int res = 0;for (int i = 2; i <= n; i++) {res = i * a;a = res;}return res;}

（2）使用缓存

	@Testpublic void testUseCache() {for (int i = 1; i <= 6; i++) {resultData = new int[i + 1];long start = System.currentTimeMillis();System.out.println(i + ":" + useCache(i) + " 所花费的时间为" + (System.currentTimeMillis() - start) + "ms");}}/*** 递归求解优化：使用缓存。时间复杂度O(n)和空间复杂度O(n)* @param n*/private static int resultData[]; // 初始换全部是0private static int useCache(int n){if(n <= 1){return 1;}if(resultData[n] > 0){return resultData[n];}int res = n * useCache(n - 1);resultData[n] = res;return res;}

（3）使用尾递归

	@Testpublic void testTailRecurve() {for (int i = 1; i <= 6; i++) {long start = System.currentTimeMillis();System.out.println(i + ":" + tailRecurve(i, 1) + " 所花费的时间为" + (System.currentTimeMillis() - start) + "ms");}}/*** 递归求解优化：使用尾递归。时间复杂度O(n)和空间复杂度O(n)* @param n* @param res - 每次保存的结果。倒着算，初始值为终止条件值* @return*/public static int tailRecurve(int n, int res) {//System.out.println(n + ":" + res);	// 倒着算的结果if (n <= 1) {return res;}return tailRecurve(n - 1, n * res);	//倒着算}

三、斐波那契数列求项

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……。这个数列，第一和第二项为1，从第 3项开始，每一项都等于前两项之和。

斐波那契数列递推的方法定义：

f(n) = f(n - 1) + f(n - 2) （n ≥ 3，n ∈ N*）
f(1) = f(2) = 1

1、递归求解

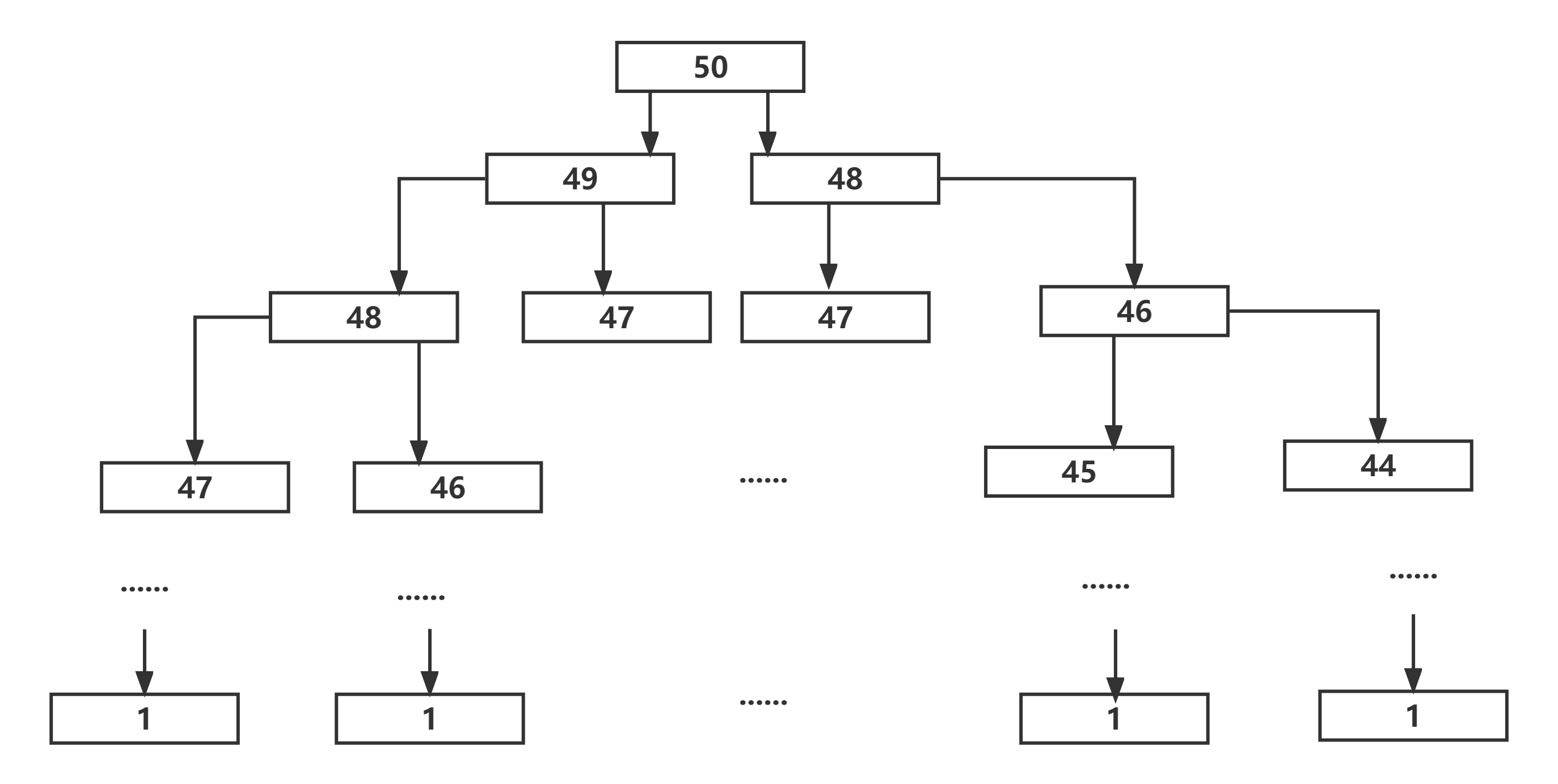
	@Testpublic void testFibonacci(){//int res = fibonacci(6);//System.out.println(res);for (int i = 1; i <= 45; i++) {long start = System.currentTimeMillis();System.out.println(i + ":" + fibonacci(i) + " 所花费的时间为" + (System.currentTimeMillis() - start) + "ms");}}/*** 递归求解：时间复杂度O(2^n)和空间复杂度O(2^n)* * @return*/private static int fibonacci(int n) {if (n <= 2) {return 1; // 递归的终止条件}return fibonacci(n - 1) + fibonacci(n - 2); // 继续递归的过程}

2、优化递归

（1）使用非递归

	@Testpublic void testNotRecurve(){for (int i = 1; i <= 45; i++) {long start = System.currentTimeMillis();System.out.println(i + ":" + notRecurve(i) + " 所花费的时间为" + (System.currentTimeMillis() - start) + "ms");}}/*** 递归求解优化：使用非递归。时间复杂度O(n)和空间复杂度O(n)* @param n*/private static int notRecurve (int n){if(n <= 2){return 1;}int a = 1;int b = 1;int res = 0;for (int i = 3; i <= n; i++) {res = a + b;a = b;b = res;}return res;}

（2）使用缓存

	@Testpublic void testUseCache() {for (int i = 1; i <= 45; i++) {resultData = new int[i + 1];long start = System.currentTimeMillis();System.out.println(i + ":" + useCache(i) + " 所花费的时间为" + (System.currentTimeMillis() - start) + "ms");}}/*** 递归求解优化：使用缓存。时间复杂度O(n)和空间复杂度O(n)* @param n*/private static int resultData[]; // 初始换全部是0private static int useCache(int n){if(n <= 2){return 1;}if(resultData[n] > 0){return resultData[n];}int res = useCache(n - 1) + useCache(n -2);resultData[n] = res;return res;}

（3）使用尾递归

	@Testpublic void testTailRecurve() {for (int i = 1; i <= 45; i++) {long start = System.currentTimeMillis();System.out.println(i + ":" + tailRecurve(i, 1, 1) + " 所花费的时间为" + (System.currentTimeMillis() - start) + "ms");}}/*** 递归求解优化：使用尾递归。时间复杂度O(n)和空间复杂度O(n)* @param n* @param res - 每次保存的结果，初始值为终止条件值。* @param pre - 上次保存的结果，初始值为终止条件值。* @return*/public static int tailRecurve(int n, int res, int pre) {  if (n <= 2) {return res;}return tailRecurve(n - 1, res + pre, res);	//倒着算}

– 求知若饥，虚心若愚。