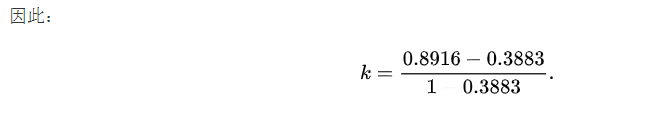评分员间可信度inter-rater reliability

在统计学中，评分员间可信度inter-rater reliability，评分员间吻合性inter-rater agreement，或一致性concordance 都是描述评分员之间的吻合程度。它对评判者们给出的评级有多少同质性homogeneity或共识consensus给出一个分值。它有助于改进人工评判辅助工具，例如确定某个范围是否适用于度量某个变量。如果评分员间不吻合，要么是这个范围不对，要么是评分员需要重新训练。

有很多统计量可以用于确定评分员间信度，不同的是适用于不同类型的度量。比方说有：吻合的联合概率joint-probability of agreement，科恩的Kappa（Cohen's kappa）及弗雷斯的Kappa（Fleiss' kappa），评分员间相关性inter-rater concordance，一致性相关系数concordance correlation coefficient 以及类间相关性intra-class correlation。

Cohen's kappa

Cohen's kappa 系数是对评分员（或标注者）间在定性（分类的）项目上的吻合性[1] 的一种统计度量。一般认为它比单纯的吻合百分比计算更健壮，因为考虑到了可预见的偶然发生的吻合。

一些研究者[2] 指出，kappa倾向于以观察到的类别种类频率为假设，会产生在也同样普遍用到的种类上的吻合被低估了的效果，处于这个原因，kappa被认为是一个对吻合过于保守的度量。而另外的研究者辩驳[3] 称kappa考虑了偶然吻合。为了有效做到这一点，就需要一个显式的模型描述偶然性是如何影响到评分员决策的。所谓的kappa统计量的偶然性调节认为：当不完全肯定时，评分员只是猜的——这是一个很不现实的方案。

计算

Cohen's kappa 度量两个评分员之间把N个项目分成C个互斥类别的吻合程度。它最早是由Galton（1892）提出的（见Smeeton（1985）[4][5]）。

κ的公式是：

其中Pr(a) 是评分员间相对观察到的吻合，而Pr(e) 是偶然吻合的假想概率，是用观察到的数据计算出的每个观察者随机选择各个种类的概率。如果评分员完全吻合，κ=1；如果评分员间除了期望的偶然发生的吻合（由Pr(e) 定义）外没有吻合，κ=0。

1960年Jacob Cohen在期刊Educational and Psychological Measurement发表文章最早将Kappa最为新技术引入。Scott（1955）提出过类似的统计量，称为Pi，与Cohen's kappa不同的是Pr(e) 的计算。注意Cohen's kappa只是度量两个评分员间的吻合，当评分员多于2的情况有对应的吻合度量——Fleiss' kappa，见Fleiss（1971），不过，它是Scott's Pi统计量在多评分员情况的泛化，而非Cohen's kappa的。

示例：

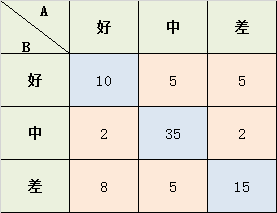
假设你在分析资助申请的数据。两个评审官读出每个资助申请并评判“yes”或“no”。假使数据如下，行是评审A，列是评审B：

		B	B
		Yes	No
A	Yes	20	5
A	No	10	15

注意，有20个申请评审A和B都批准了，而有15个申请两个评审同时拒绝了。因此，观察得到的吻合百分比是Pr(a)=（20+15）/50=0.7

计算随机吻合的概率Pr(e) 时我们看到：

评审A批准和拒绝的申请各25个，即比例各50%。
评审B批准30个申请，拒绝20个，即批准的比例60%。

因此，他俩同时批准的随机概率就是0.5*0.6=0.3，而俩人同时拒绝的随机概率是0.5*0.4=0.2。于是随机吻合的总体概率Pr(e)=0.3+0.2=0.5。应用Cohen's kappa 公式得到：

$\κ= \压裂{\ PR（A） - \镨（E）} {1 - \镨（E）} = \压裂{0.70-0.50} {1-0.50} = 0.40 \！$

百分比相同，但数值不同

Cohen's Kappa 在一个情况下会出问题，即比较这样两对评分员间Kappa 值：两对有相同的吻合百分比，但一对的评级数相近，而另一对的评级数相差则很大[6]。比如下面这个例子，两组数据中A 和B 的吻合相同（都是60/100），于是我们期望相应的Cohen's Kappa 值反映这一点。

	Yes	No
Yes	45	15
No	25	15

	Yes	No
Yes	25	35
No	5	35

但是实际计算结果显示，第二组中A与B 相似度比第一组大。

显著性差异Significance和大小magnitude

统计显著性差异既没有声称在一个指定应用中的大小如何重要，也没有声称什么样的被视为吻合程度高还是低。Kappa 的统计显著性差异极少被提及，可能是因为即使相对较低的Kappa 值仍然显著异于0，但也还没有大到足以满足调查 [7]:66 。不过，不同的计算程序还是描述[8]和计算[9]了它的标准误差。

既然统计显著性差异不是有用的指标，那么Kappa 多大才反映足够吻合？准则是有用的，但除了吻合其他的因素也能影响其大小，这对一个有疑问的大小给出了解释。Sim 和Wright 指出，（编码是等概率或其概率变化）的发生率（prevalence）以及（两观察者/评分员异同的边缘概率）偏差（bias）是两个重要的因素。当其他因素相同时，编码是等概率的且在两个观察者/评分员的分布相似，Kappa 值会比较高 [10]:261-262 。

另一个因素是编码数量。编码增加，Kappa随之变高。基于模拟研究，Bakeman 及其同事得出结论：对容易犯错的观察者/评分员，编码越少Kappa 值越低。而且，与Sim & Wright 关于发生率prevalence的表述一致，编码严格等概率时Kappa 值更高。因此Bakeman 等人总结说“没有一个Kappa 值是被普遍接受的”[11]:357。他们甚至提供了一个程序，从特定的编码数量及其概率和观察者精度计算出Kappa 值。如：设等概率编码且观察者85%的准确率，当编码数分别为2、3、5、10时，kappa 值对应是0.49、0.60、0.66、0.69。

虽然如此，一些文献还是提出了大小准则。第一个大概是Landis和Koch [12]，他们这样划分：值<0为不吻合，0~0.20轻微slight，0.21~0.40正常fair，0.41~0.60中度moderate吻合，0.61~0.80可观substantial，0.81~1几乎完全吻合。但这一套划分准则并没有被普遍接受；Landis 和Koch 是只是主观判定，没有给出证据支持。人们注意到这些准则可能弊大于利 [13]。Fleiss [14]:218 的准则同样武断地将Kappa 值划分为大于0.75为优秀，0.40~0.75为正常至良好，低于0.40为差。

加权Kappa

加权Kappa用于计算不同的分歧 [15]，当编码是有序的情况下尤其有用 [7]:66。涉及三个矩阵：观察到的评分矩阵、基于随机吻合的期望评分矩阵、以及权重矩阵。权重矩阵对角线上的单元代表吻合，因此由0构成。非对角单元中的权重值代表分歧的严重程度。通常，单元距离对角线为1时权重设为1，距离为2的单元权重设2，一次类推。

加权κ的计算公式为：

其中，k是编码数量，、、分别是权重、观察值、期望矩阵的元素。当权重矩阵对角线元素为0，非对角线元素为1时，公式就退化成上面提到的Kappa公式。

Kappa 最大值

Kappa 假定其理论最大值是1，当且仅当俩观察者的编码分布相同，即对应的行和列的和相等。尽管如此，假定分布不相同所能达到的最大Kappa 值有助于解释实际获得的kappa值。

Kappa 最大值方程是：

其中，，一般，，k 是编码数，是行概率，而是列概率。

另见

Fleiss‘s Kappa
类间相关性 Intraclass correlation

参考文献

^Carletta, Jean. (1996) Assessing agreement on classification tasks: The kappa statistic. Computational Linguistics, 22(2), pp. 249–254.
^Strijbos, J.; Martens, R.; Prins, F.; Jochems, W. (2006). "Content analysis: What are they talking about?".Computers & Education 46: 29–48.doi:10.1016/j.compedu.2005.04.002.
^Uebersax JS. (1987)."Diversity of decision-making models and the measurement of interrater agreement" (PDF). Psychological Bulletin101: 140–146.doi:10.1037/0033-2909.101.1.140.
^Galton, F. (1892). Finger PrintsMacmillan, London.
^Smeeton, N.C. (1985). "Early History of the Kappa Statistic".Biometrics41: 795.
^Kilem Gwet (May 2002)."Inter-Rater Reliability: Dependency on Trait Prevalence and Marginal Homogeneity". Statistical Methods for Inter-Rater Reliability Assessment2: 1–10.
^^a^bBakeman, R.; & Gottman, J.M. (1997).Observing interaction: An introduction to sequential analysis(2nd ed.). Cambridge, UK: Cambridge University Press. ISBN0-521-27593-8.
^Fleiss, J.L.; Cohen, J., & Everitt, B.S. (1969). "Large sample standard errors of kappa and weighted kappa".Psychological Bulletin 72: 323–327.doi:10.1037/h0028106.
^Robinson, B.F; & Bakeman, R. (1998). "ComKappa: A Windows 95 program for calculating kappa and related statistics".Behavior Research Methods, Instruments, and Computers 30: 731–732.doi:10.3758/BF03209495.
^Sim, J; & Wright, C. C (2005). "The Kappa Statistic in Reliability Studies: Use, Interpretation, and Sample Size Requirements".Physical Therapy 85: 257–268.PMID15733050.
^Bakeman, R.; Quera, V., McArthur, D., & Robinson, B. F. (1997). "Detecting sequential patterns and determining their reliability with fallible observers".Psychological Methods 2: 357–370.doi:10.1037/1082-989X.2.4.357.
^Landis, J.R.; & Koch, G.G. (1977). "The measurement of observer agreement for categorical data".Biometrics 33 (1): 159–174.doi:10.2307/2529310.JSTOR2529310. PMID843571.
^Gwet, K. (2010). "Handbook of Inter-Rater Reliability (Second Edition)" ISBN 978-0-9708062-2-2^{[page needed]}
^Fleiss, J.L. (1981).Statistical methods for rates and proportions(2nd ed.). New York: John Wiley.ISBN0-471-26370-2.
^Cohen, J. (1968). "Weighed kappa: Nominal scale agreement with provision for scaled disagreement or partial credit".Psychological Bulletin 70 (4): 213–220. doi:10.1037/h0026256.PMID19673146.
^Umesh, U.N.; Peterson, R.A., & Sauber. M.H. (1989). "Interjudge agreement and the maximum value of kappa.".Educational and Psychological Measurement 49: 835–850.doi:10.1177/001316448904900407.

Banerjee, M.; Capozzoli, Michelle; McSweeney, Laura; Sinha, Debajyoti (1999). "Beyond Kappa: A Review of Interrater Agreement Measures".The Canadian Journal of Statistics / La Revue Canadienne de Statistique27 (1): 3–23. JSTOR3315487.
Brennan, R. L.; Prediger, D. J. (1981). "Coefficient λ: Some Uses, Misuses, and Alternatives".Educational and Psychological Measurement 41: 687–699.doi:10.1177/001316448104100307.
Cohen, Jacob (1960). "A coefficient of agreement for nominal scales".Educational and Psychological Measurement 20(1): 37–46.doi:10.1177/001316446002000104.
Cohen, J. (1968). "Weighted kappa: Nominal scale agreement with provision for scaled disagreement or partial credit".Psychological Bulletin 70 (4): 213–220. doi:10.1037/h0026256.PMID19673146.
Fleiss, J.L. (1971). "Measuring nominal scale agreement among many raters".Psychological Bulletin 76 (5): 378–382.doi:10.1037/h0031619.
Fleiss, J. L. (1981) Statistical methods for rates and proportions. 2nd ed. (New York: John Wiley) pp. 38–46
Fleiss, J.L.; Cohen, J. (1973). "The equivalence of weighted kappa and the intraclass correlation coefficient as measures of reliability".Educational and Psychological Measurement 33: 613–619.doi:10.1177/001316447303300309.
Gwet, K. (2008)."Computing inter-rater reliability and its variance in the presence of high agreement". British Journal of Mathematical and Statistical Psychology61 (Pt 1): 29–48.doi:10.1348/000711006X126600.PMID18482474.
Gwet, K. (2008)."Variance Estimation of Nominal-Scale Inter-Rater Reliability with Random Selection of Raters". Psychometrika73(3): 407–430. doi:10.1007/s11336-007-9054-8.
Gwet, K. (2008). "Intrarater Reliability." Wiley Encyclopedia of Clinical Trials, Copyright 2008 John Wiley & Sons, Inc.
Scott, W. (1955). "Reliability of content analysis: The case of nominal scale coding".Public Opinion Quarterly 17: 321–325.
Sim, J.; Wright, C. C. (2005). "The Kappa Statistic in Reliability Studies: Use, Interpretation, and Sample Size Requirements".Physical Therapy85 (3): 257–268. PMID15733050.