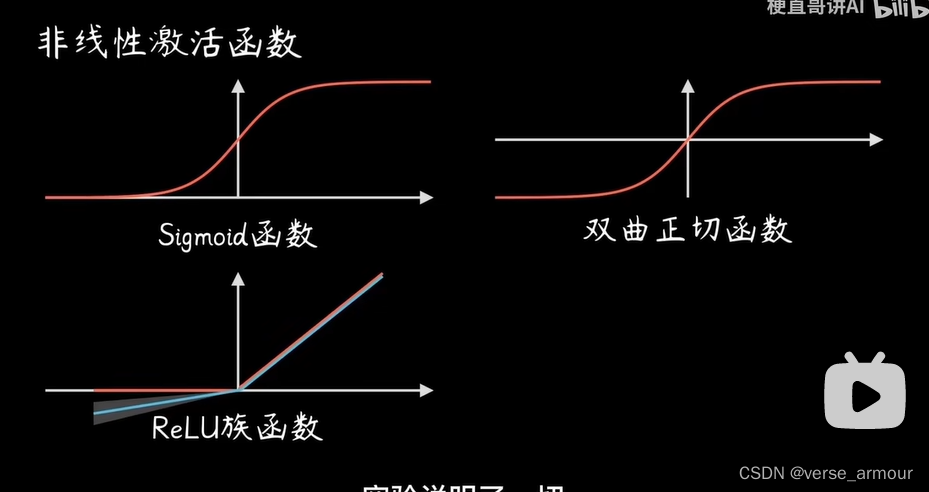
@[]

1. 对卷积最朴素的理解

首先我们在教材上看到的卷积公式是$\int f(\tau )g(x-\tau )d\tau$。对于这个公式的理解，网上有很多讲解视频，都是用一些具体的例子来帮助我们理解卷积的过程。推荐b站上的视频1, 视频2。

有了一些比较具体的例子以后，我们总结一下卷积主要涉及到两个函数：

• f(): 我们发现f是一个不稳定的输入
• g(): 对于每个entity，我们发现他们都遵循相同的发展规律，也就是g()。所以g()可以视为稳定的。

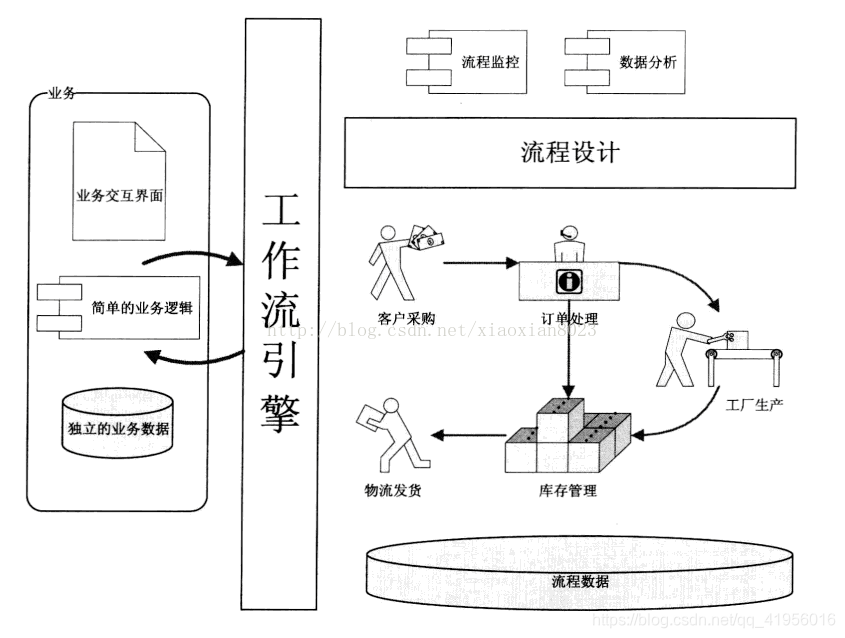
那么卷积就是截止到x，所有的研究对象的状态的加和。为什么叫卷积，因为我们发现f里面的函数$\tau$和g里面的$x-\tau$相加是确定的。一个是$\tau$，一个是$-\tau$，所以涉及到一个反转。f和g对应的自变量是相反的方向。可以看下图（截取自b站王木头学科学）

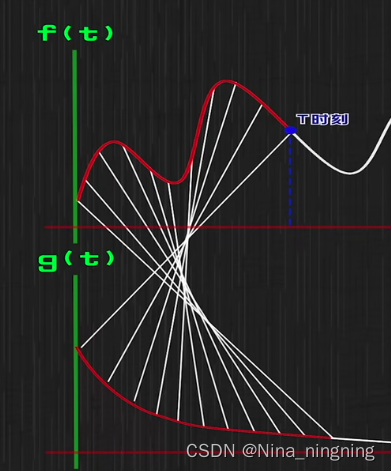
接下来我们可以看看卷积在卷积神经网络中的含义

2. 卷积神经网络

如果还不了解卷积神经网络的，可以先看看我的上一篇博文,先对卷积神经网络有一个大致的了解以后，我们首先想到的问题（这应该也是导师或者找工作面试中经常会问的问题）。卷积神经网络中的“卷积”体现在哪里？

回顾卷积神经网络，我们用到一个卷积核的东西，然后和原图像上的每个小的matrix计算得到一个新的值。这里有三个要素可以和一般的卷积对应：

• 卷积核：对应f函数，它是相对不变的
• 原图上的每个小的matrix：对应g函数，它是相对来说不稳定的。
• 滑动滚动扫描图上的每个小的matrix：相当于积分操作，只不过这里是离散的。
  对于卷积神经网络，不同的卷积核对应不同的结果：
• 平滑卷积核：平滑卷积核的话，相当于对图上的每个小的matrix元素加和求平均。大家可以想象一下这样的到新的图像，将会比原来的图像更加的平滑。比如对于一张高清图片来说，可能细小的毛孔都可以看到，但是这样操作以后，毛孔就被弱化了，看起来就是朦胧的美。
• filter：当然，在卷积神经网络当中，我们选择的卷积核都是某一种特征，那么卷积核和原图上的每个元素做计算，其实就是在对比原图上的每个小的matrix和卷积核的相似程度。达到特征提取的目的。

3. 图卷积神经网络

图卷积神经网络，其中也用到卷积，这里面涉及到傅立叶分析，卷积在傅立叶空间上变成乘法，会更加简单。