K均值聚类算法

无监督学习

在一个典型的监督学习中，我们有一个有标签的训练集，我们的目标是找到能够区分正样本和负样本的决策边界，在这里的监督学习中，我们有一系列标签，我们需要据此拟合一个假设函数。

与此不同的是，在非监督学习中，我们的数据没有附带任何标签，我们拿到的数据就是这样的：

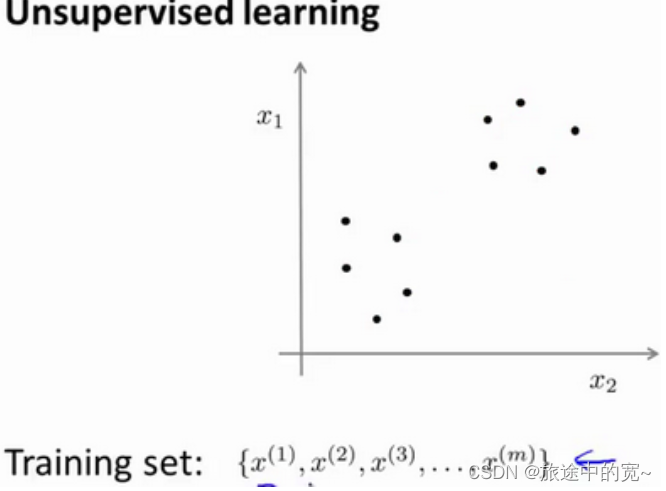
在这里我们有一系列点，却没有标签。

因此，我们的训练集可以写成只有 $x^{(1)}\;,\;x^{(2)}\;\cdots\;x^{(m)}$ 。我们没有任何标签 $y$ 。因此，图上画的这些点没有标签信息。

也就是说，在非监督学习中，我们需要将一系列无标签的训练数据，输入到一个算法中，然后我们告诉这个算法，快去为我们找找这个数据的内在结构给定数据。

我们可能需要某种算法帮助我们寻找一种结构。

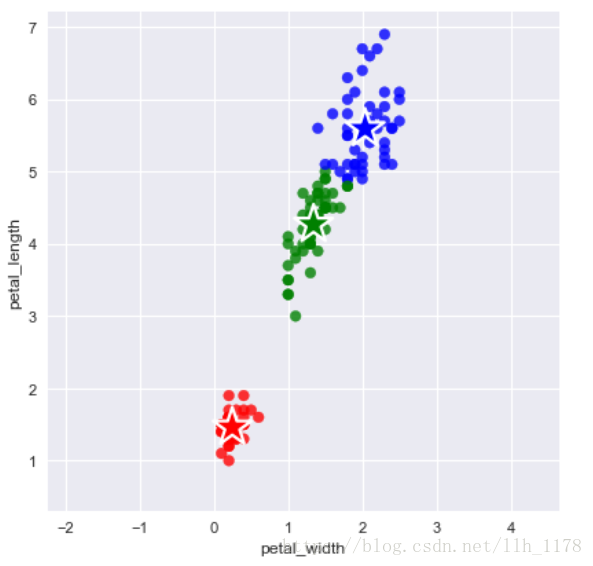
图上的数据看起来可以分成两个分开的点集（称为簇），一个能够找到我圈出的这些点集的算法，就被称为聚类算法。

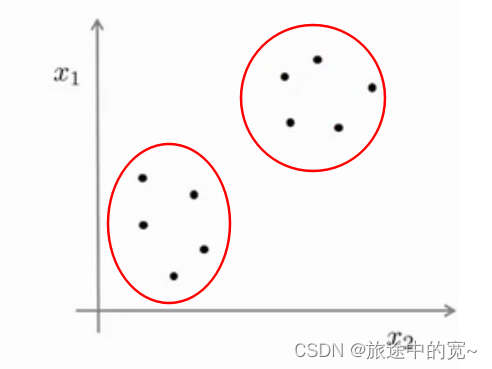
当然，此后我们还将提到其他类型的非监督学习算法，它们可以为我们找到其他类型的结构或者其他的一些模式，而不只是簇。

我们将先介绍聚类算法。

K-均值算法

K-均值是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。

假设我有一个无标签的数据集，并且我想将其分成两个簇，现在我利用K均值算法。具体操作如下:

第一步是随机生成两点，这两点就叫做聚类中心，也就是图上两个叉:

我选取两个点的原因是因为我想将我的数据聚成两类。

K-均值算法是一个迭代算法，它会去做两件事情:第一个是簇分配，第二个是移动聚类中心。

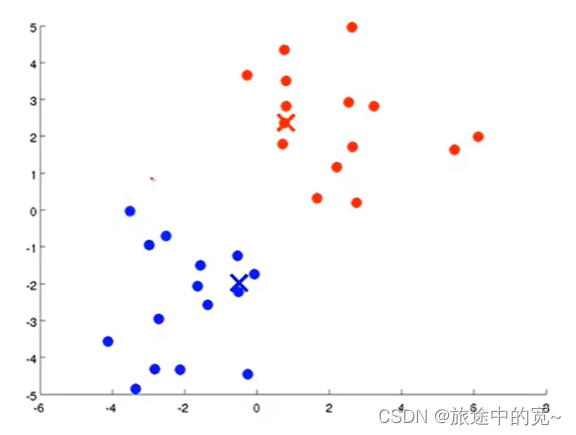
K均值算法中，每次内循环的第一步就是要进行簇分配。也就是说，我要遍历每个样本，也就是图上的每个绿色的点，然后根据每一个点是与红色聚类中心更近还是与蓝色聚类中心更近来将每个数据点分配给两个聚类中心之一。

具体来说，就是要遍历我们的数据集，然后将每个点染成红色或者蓝色，这取决于某个点是离红色更近还是蓝色更近。

内循环的第二步是移动聚类中心。

我们要做的是将两个聚类中心，也就是上面红蓝两个叉将其移动到同色的点的均值处。因此我们要做的是找出所有红色的点然后计算它们的均值，也就是所有红色的点的平均位置，然后将红色聚类中心移动到这里。蓝色聚类点实行同样的操作。

接下来我们重复上面的步骤，直到最后完成要求:

K-均值是一个迭代算法，假设我们想要将数据聚类成n个组，其方法为:

1.首先选择K个随机的点，称为聚类中心（cluster centroids）

2.对于数据集中的每一个数据，按照距离K个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类。

3.计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置

4.重复步骤2-4直至中心点不再变化

我们用 $\mu^1\;,\;\mu^2\;\cdots\;\mu^k$ 来表示聚类中心，用 $c^{(1)}\;,\;c^{(2)}\;,\;\cdots\;,\;c^{(m)}$ 来存储与第 $i$ 个实例数据最近的聚类中心的索引，K-均值算法的伪代码如下：

x 
Repeat{for i = 1 to m: c(i):=index(from 1 to k) of cluster centroid
closest to x(i) 
for k = 1 to K: μk := average (mean) of points assignedto cluster k 
}

算法分为两个步骤，第一个for循环是赋值步骤，即：对于每一个样例 $i$ ，计算其应该属于的类。第二个for循环是聚类中心的移动，即：对于每一个类K，重新计算该类的质心。

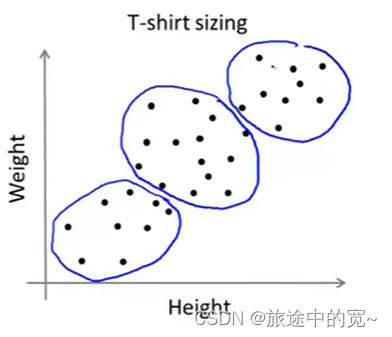
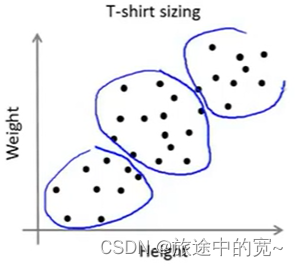
K-均值算法也可以很便利地用于将数据分为许多不同组，即使在没有非常明显区分的组群的情况下也可以。下图所示的数据集包含身高和体重两项特征构成的，利用K-均值算法将数据分为三类，用于帮助确定将要生产的T-恤衫的三种尺寸。

优化目标

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此
K-均值的代价函数（又称畸变函数 Distortion function）为：
$J(c^{(1)}\;,\;c^{(2)}\;,\;\cdots\;,\;,c^{(m)}\;,\;\mu_1\;,\;\mu_2\;,\;\cdots\;,\;\mu_K)=\frac{1}{m}\sum_{i=1}^{m}||X^{(i)}-\mu_{c^{(i)}}||^2$

其中 $\mu_{c^{(i)}}$ 代表与 $x^{(i)}$ 最近的聚类中心点。
我们的的优化目标便是找出使得代价函数最小的 $c^{(1)}\;,\;c^{(2)}\;,\;\cdots\;,\;,c^{(m)}$ 和 $\mu_1\;,\;\mu_2\;,\;\cdots\;,\;\mu_K$ :
$\min_{c^{(1)}\;,\;\cdots\;,\;c^{(m)}\;,\;\mu_1\;,\;\cdots\;,\;\mu_K}\;J(c^{(1)}\;,\;c^{(2)}\;,\;\cdots\;,\;,c^{(m)}\;,\;\mu_1\;,\;\mu_2\;,\;\cdots\;,\;\mu_K)$

回顾刚才给出的:
K-均值迭代算法，我们知道，第一个循环是用于减小 $c^{(i)}$ 引起的代价，而第二个循环则是用于减小 $\mu_i$ 引起的代价。迭代的过程一定会是每一次迭代都在减小代价函数，不然便是出现了错误。

随机初始化

接下来讨论一下如何初始化K均值聚类算法，更重要的是，这将引导我们如何使算法避免局部最优解。

这是我们的K均值算法:

其中我们没有讨论的就是最开始的如何初始化聚类中心，有几种不同的方法可以用来随机初始化聚类中心。

但是，事实证明，有一种方法比其他大多数可能考虑到的方法更值得推荐。

我们通常是这样初始化聚类中心的:
（1）我们应该选择 $K < m$ ，即聚类中心点的个数要小于所有训练实例的数量
（2）随机选择K个训练实例，然后令K个聚类中心分别与这K个训练实例相等

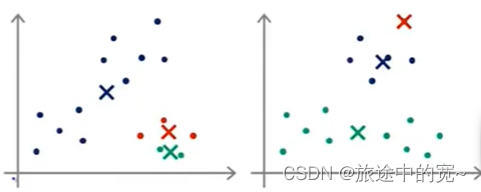
具体来说，K均值算法可能会落在局部最优，这取决于初始化的情况。我们给出下面的例子:

我们可能的分类如下:

为了解决这个问题，我们通常需要多次运行K均值算法，每一次都重新进行随机初始化，最后再比较多次运行K均值的结果，选择代价函数最小的结果。

以下是具体的做法:

这种方法在K较小的时候还是可行的，但是如果K值较大，这么做也是不会有明显的改善。

选择聚类数

如何去选择聚类数量或者说如何去选择参数K的值？

说实话，这个问题没有什么好的答案，也没有能自动处理的方法。

目前为止，用来决定聚类数量最常用的方法仍然是通过观察可视化的图或者通过观察聚类算法的输出等等。

我们举上面的例子来看，对于上面的数据集，我们该如何选择聚类中心的数目，是选择K=2还是选择K=4？

当人们在讨论选择聚类数量的方法时，有一个可能会谈及的方法叫作“肘部法则”。

关于“肘部法则”，我们所需要做的是改变K值，也就是聚类类别数目的总数。我们用一个聚类来运行K均值聚类方法。这就意味着，所有的数据都会分到一个聚类里，然后计算成本函数或者计算畸变函数J。K代表聚类数字。

我们可能会得到一条类似于这样的曲线。像一个人的肘部。这就是“肘部法则”所做的，让我们来看这样一个图，看起来就好像有一个很清楚的肘在那儿。好像人的手臂，如果你伸出你的胳膊，那么这就是你的肩关节、肘关节、手。这就是“肘部法则”。你会发现这种模式，它的畸变值会迅速下降，从1到2，从2到3之后，你会在3的时候达到一个肘点。在此之后，畸变值就下降的非常慢，看起来就像使用3个聚类来进行聚类是正确的，这是因为那个点是曲线的肘点，畸变值下降得很快，K=3之后就下降得很慢，那么我们就选K=3。当你应用“肘部法则”的时候，如果你得到了一个像上面这样的图，那么这将是一种用来选择聚类个数的合理方法。

但是我们有时会得到一条模糊的曲线，如下图所示: