此博客是抄论文的，你可以认为是转载的

1.线性递推数列

有限数列显然是线性递推数列。
无限数列$a_i$设其生成函数为$A(x)$
那么如果$A(x)$能被表示为$\frac{C(x)}{B(x)}$的形式，其中$B(x)[x^0]=1$，则$A(x)$是线性递推数列。
常数项为$1$是因为递推式你要让${\sum }_{j=0}{b}_j{a}_{i-j}=0$来递推出$a_i$所以常数项需要为$1$。
能这样表示是因为线性递推实质上就是$A(x)B(x)=C(x)$，其中$B(x)$是我们的线性递推式。

对于一个线性递推数列$a_i$，假设他前$i$项的最短递推式是$R^{(i)}$，长度为$l_i$，那么如果$R^{(i-1)}$不是前$i$项的最短递推式，那么有$l_i\ge \max (l_{i-1},i+1-l_{i-1})$，且这个等号是可以通过构造取到的。
首先$l_i\ge l_{i-1}$显然，如果$l_i\le i-l_{i-1}$的话：

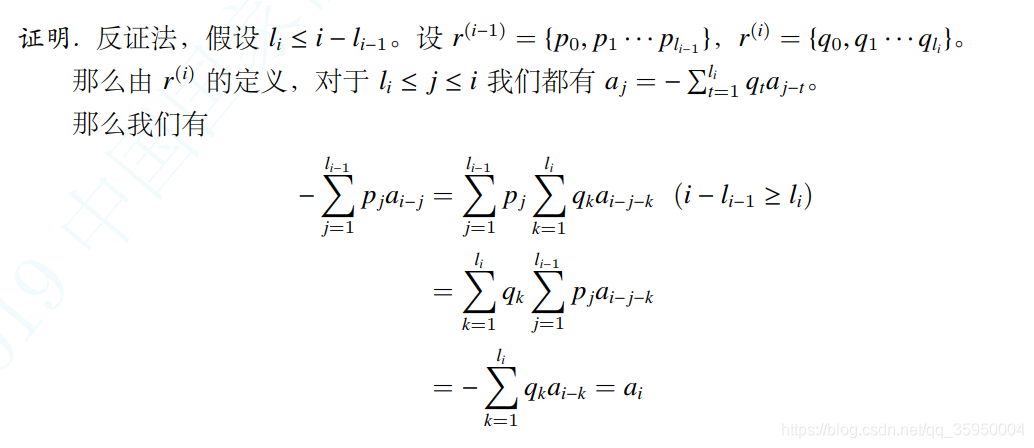
实在不知道怎么用语言表示交换和号。
也就是说如果$l_i\le i-l_{i-1}$那么原来的递推式必可以继续用。

接下来我们给出在$R^{(i-1)}$不是前$i$项的递推式时$l_i=\max (l_{i-1},i+1-l_{i-1})$的构造方案，也就是$BM$算法。

也就是说每次增长递推式，我们都可以用这个方法使得增长时$l_i=\max (l_{i-1},i+1-l_{i-1})$，不增长时$l_i=l_{i-1}$。
因为上文证明了$l_i\ge \max (l_{i-1},i+1-l_{i-1})$，所以这个算法对于有限长度的数列求出的递推式一定是最短的。

对于无限长的数列，

所以我们只需要取最短递推式长度的两倍即可。
边界情况：第一次增长递推式的时候，$a_i$应该是第一个非$0$元素，那么$l_i=i$个$0$即为前$i$个数的最短递推式，也就是根本没有递推，同时也满足$l_i\ge i+1-l_{i-1},(l_{i-1}=0)$。
这里需要纠正一个错误观念，一个最短线性递推式的最后一项是可以为$0$的，因为假如一个长度为$n$的递推式$F(x)$对于$a_n={\sum }_{i=1}^{n}F(x)[x^i]a_{n-i}$不成立，我们需要在递推式的最后补一个$0$，这样$a_n$就不在递推式成立的范围内。
也就是说一个线性递推数列被表示为$\frac{S(x)}{R(x)}$的形式，则它的递推式的长度是$R(x)$的次数和$S(x)$的次数加一取$\max$。

线性递推求第$n$项：

代码：luogu【模板】Berlekamp-Massey算法

$\mathcal{C}ode:$(真的很短。)

#include<bits/stdc++.h>
#define rep(i,j,k) for(int i=(j),LIM=(k);i<=LIM;i++)
#define per(i,j,k) for(int i=(j),LIM=(k);i>=LIM;i--)
#define maxn 10005
#define pb push_back
#define vi vector<int>
#define mod 998244353
using namespace std;int n,m,a[maxn];
int Pow(int b,int k){ int r=1;for(;k;k>>=1,b=1ll*b*b%mod) if(k&1) r=1ll*r*b%mod;return r; }
vi BM(int *a,int n){ // a[0 ~ n] is usedvi r(1,1),p,t;int lt;rep(i,0,n){int d=0;rep(j,0,r.size()-1) d = (d + r[j] * 1ll * a[i-j]) % mod;		if(!d) continue;t = r;r.resize(max(r.size() , i+2-(r.size()-(r.size()!=0))));rep(j,0,p.size()-1) r[j+i-lt] = (r[j+i-lt] - 1ll * d * p[j]) % mod;int iv = Pow(d , mod-2);p = t , lt = i;rep(i,0,p.size()-1) p[i] = 1ll * p[i] * iv % mod;}return r; // a \times r = const 
}
typedef vi poly;
poly Mul(const poly &A,const poly &B,const poly &P){poly r(A.size() + B.size() - 1);rep(i,0,A.size()-1) rep(j,0,B.size()-1) r[i+j] = (r[i+j] + 1ll * A[i] * B[j]) % mod;per(i,r.size()-1,P.size()-1) if(r[i]){// in this problem P[P.size()-1] = 1 , so there is no need to getinv.int t = r[i];rep(j,1,P.size())r[i-j+1] = (r[i-j+1] - 1ll * P[P.size()-j] * t) % mod;}r.resize(P.size()-1);return r;
}int main(){scanf("%d%d",&n,&m);rep(i,0,n-1) scanf("%d",&a[i]);vi P = BM(a,n-1);rep(i,1,P.size()-1) printf("%d%c",(mod-(P[i]+mod)%mod) % mod," \n"[i==P.size()-1]);reverse(P.begin(),P.end());poly r(1,1),t(2,0);t[1] = 1;for(;m;m>>=1,t=Mul(t,t,P)) if(m&1)r = Mul(r,t,P);int ans = 0;rep(i,0,r.size()-1) ans = (ans + 1ll * r[i] * a[i]) % mod;printf("%d\n",(ans+mod)%mod);
}

向量序列的最短递推式：

矩阵的零化多项式：使得矩阵$M$：
$f(M)={\sum }_{i=0}^n{a}_i{M}^i=0$
矩阵的最小多项式：
零化多项式中次数最低的多项式。
如何求矩阵的最小多项式：
直接求$I,M,M^2...$的最短递推式即可，对于稀疏矩阵可以做到$O(n(n+e))$。

BM与矩阵的特征多项式：
特征多项式是矩阵的一个零化多项式，
而$BM$求出的最小多项式也是矩阵的一个零化多项式

最小多项式是特征多项式的一个因式，因为如果不是则可以做带余除法得到余式为更小的零化多项式。
对于一个线性递推问题，我们可以通过零化多项式得到线性递推式，所以在解决线性递推时可以找最小多项式（用BM），也可以求特征多项式。
但是特征多项式的最经典的解法是根据定义$|\lambda -IE|=0$来求行列式后拉格朗日插值求出多项式，$O(n^4)$相较于$BMO(n^3)$感觉没有什么竞争力，尽管特征多项式有$O(n^3)$的巧妙解法，但是这个解法无法计算出线性递推的前$n$项（就是不能用递推式的部分），有了前$n$项那为什么不用$BM$呢？
综上在信息学奥赛的当前时代最小多项式完爆特征多项式，很多打着特征多项式的旗子的题目都可以用BM解决。

接下来我们看一个例题：
「2018 集训队互测 Day 1」完美的旅行
$n$个点的有向图，一次旅行是走$a\ge 1$步，愉悦值为起点和终点的编号$and$和。
多次旅行的愉悦值是每次旅行的$and$和，对于所有的愉悦值$0\le x<n$和$1\le a\le m$的总步数，求愉悦值为$x$总步数为$a$的多次旅行方案数。

先求$and$为集合$S$的超集的方案数$f_S$，然后用$FMT$一次就可以求出$and$为集合$S$的方案数。
$and$为集合$S$的超集的一次旅行走了$a$步，可以发现就是邻接矩阵$A$的$a$次方的一些位置的和。
大小为$n$的矩阵一定有次数$\le n$的特征多项式，所以一次旅行的走了$a$步的那些答案就是一个$n$阶线性递推。
假设一次旅行的生成函数为$G(x)$，则多次旅行的生成函数为$F(x)=\frac{1}{1-G(x)}$
因为$G(x)$为$n$阶递推，所以$G(x)=\frac{S(x)}{R(x)}$，其中$R(x)$次数$\le n$,$S(x)$次数$\le n-1$。
$F(x)=\frac{R(x)}{R(x)-S(x)}$，分子次数可以为$n$，所以$F(x)$是$n+1$阶线性递推。

2.整式递推数列