一、前言

二、直线函数的形式化表示

2.1 直线被方程表示

2.2 直线被图表表示

2.3 直线的表格表示

三、hough变换的提出

3.1 极坐标表示点和线

四、 hough变换的原理

4.1 极坐标的编辑表格

4.2 用编辑平面表示：过任意点P(x,y)做所有射线，其过原点的垂足点的轨迹

4.3 构建hough算法表格（在编辑图）

五、图像处理中，Hough变换如何应用

5.1 python程序代码

5.2 实验和效果1：输入直线图片

5.3 实验效果2：输入一个点

一、前言

别看Hough变换似乎简单，但是，不发挥一下数学理论的功力是不可能理解的；本人早十几年前就用Hough，也一直想写Hough变换，但一懒就是10几年，乘春节前有空，就将Hough的详细细节揭秘出来，供大家参考。

二、直线函数的形式化表示

我们常用的二维坐标空间是笛卡尔空间，这一般无需强调；问题是对于同一个事物（比如直线）有无其它表述方式，有，并且很多。

2.1 直线被方程表示

在直角坐标系，任意一条直线的方程是

$\begin{equation} \label {eq:someequation} y= kx + b \end{equation} \; \;\;\;\;\;\;( 1 )$

2.2 直线被图表表示

在现实图像中，我们可以把等式 $\begin{equation} \label {eq:someequation} y= kx + b \end{equation}$ 看成一个表格，如图：

2.3 直线的表格表示

以上直线方程构成表格是：

因此，以上用三种方法表示一个直线内容，也就是告诉我们，函数可以以多种方式存在，而计算机算法，常常以表格的方式解决问题为妥。而且从一种表格等价地转换成另一种表格。hough变换就是这样的实例。

三、hough变换的提出

以上方程，固定k和b，能够找出线上任意一个点，这是一个正向问题；逆向问题是，给出一群点（x，y);问这些点是否构成直线？

如果试图用计算机解决，那么需要找出某种条件模式，使得所有在直线上的点(x,y）满足这种条件，不在直线的点不满足这个条件。

这里首先要强调一个事实： $r =x\cdot sin\theta + y\cdot cos\theta$ 这个式子有多重含义，如果理解错了，就无法真正懂得houghj变换，本文将逐一讲述该式的三个场景，从而排除干扰，让大家真正懂得hough变换中 $r =x\cdot sin\theta + y\cdot cos\theta$ 的意义。

3.1 极坐标表示点和线

令一个极坐标系与直角坐标系在原点重合；在极坐标上表示 $P(x,y)$ 为 $P(r,\theta )$

因此有： $y=r sin\theta \;\;\;\;x = rcos\theta$

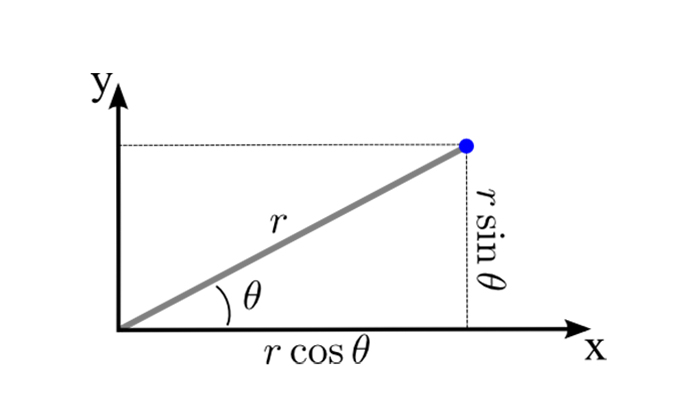
Motion basics: Difference between Cartesian and polar coordinate systems

$r = r(sin^2\theta + cos^2\theta )=rsin\theta\cdot sin\theta +rcos\theta \cdot cos\theta$

因此，

$r =x\cdot sin\theta + y\cdot cos\theta \;\;\;\;\;\;\;\;\;\;\;\;(2)$

注意：以上2）式似乎很明确直观，但是这不是hough的要点。为了追究到底 $r =x\cdot sin\theta + y\cdot cos\theta$ 是个啥意思，这里专门列出三个意义，比较三个意义之后，才能肯定，哪个解释才是hough的本意。

下面将一一描述。

1）构成点：固定x，y，且 $tg\theta =y/x$ ；表示直角坐标点 $P(x,y)$ 和极坐标 $P(r,\theta )$ 的转换公式：

$\left\{\begin{matrix} &r =x\cdot sin\theta + y\cdot cos\theta &(3) \\ &tg\theta =y/x &(4) \end{matrix}\right.$

以上（3）和（4）两个条件决定了直角坐标点 $P(x,y)$ 和极坐标 $P(r,\theta )$ 的转换公式。显然，这里我们不是研究单点的，因而这个解释不是hough变换。

2）构成圆轨迹：把 $P(x,y)$ 的x和y看成固定点，让 $\theta$ 随意变动后，r构成圆轨迹

当上面条件（3）和（4）中，去掉（4），单独保留（3）是个啥？提前告诉大家是一个圆轨迹。证明如下：

${\begin{cases} r =x\cdot sin\theta + y\cdot cos\theta \end{cases}(3)}$

${\begin{cases} r =\sqrt{x^2+y^2}(\frac{x}{\sqrt{x^2+y^2}}\cdot cos\theta + \tfrac{y}{\sqrt{x^2+y^2}}\cdot sin\theta) & (5) \end{cases} }$

令：

${\begin{cases}cos\alpha =\frac{x}{\sqrt{x^2+y^2}} \\ sin\alpha =\frac{y}{\sqrt{x^2+y^2}} \\ {\sqrt{x^2+y^2}}=D \end{cases}}$

${\begin{cases} r =D(cos\alpha \cdot cos\theta + sin\alpha \cdot sin\theta) \end{cases} }=D \cdot cos(\theta - \alpha )$

此为圆的极坐标方程，如图：

事实上，从P（x，y）引出的所有直线，都和此圆相交，如图：

结论1：所谓的 $r =x\cdot sin\theta + y\cdot cos\theta$ 就是给定P(x,y)点后，x和y固定，P与原点O构成线段为直径的圆的轨迹。

推论：过P点的任意直线，与过原点垂线的交点（垂足点），刚好落在圆 $r =x\cdot sin\theta + y\cdot cos\theta$ 上。

3）构成直线方程：给定任意直线，其到原点距离是固定的、从原点引出垂线方向角也固定

假设，有任意一条直线，如何在极坐标系表示这条直线的轨迹？

对于任意直线L，做L的垂线，且过原点，垂足为Q(x0,y0);OQ就是原点到L的距离；在直线L上找任意点P(x,y)；显然OS=x；PS=y；做OS和PS到OQ的投影，投影线为OR和RQ（=ST），显然OR+ST=OQ；

$OQ=OR+ST=xcos\alpha + ysin\alpha \\ r = xcos\cdot\alpha + y\cdot sin\alpha\: \: \: \: \: (7)$

结论：公式（7）的意义是，一条直线上所有的点都与一个r和一个 $\alpha$ 对应，这个解释才是我们这里hough变换所指的意义！

注意：很神奇！ $r =x\cdot sin\theta + y\cdot cos\theta$ 居然有三种不同含义，以上三个解释全部摆出，经对比，式（7）才是我们要的hough变换的含义。

四、 hough变换的原理

4.1 极坐标的 $r-\theta$ 表格

将极坐标的r和 $\theta$ 以直角方式构建坐标，就成了 $r-\theta$ 表格平面；直角坐标平面x-y平面的任意点一一对应于 $r-\theta$ 平面的点。

在 $r-\theta$ 平面上， $\theta$ 坐标是个 $0-2\pi$ 的有限区间，这是大大的有利条件！！！

4.2 用 $r-\theta$ 平面表示：过任意点P(x,y)做所有射线，其过原点的垂足点的轨迹

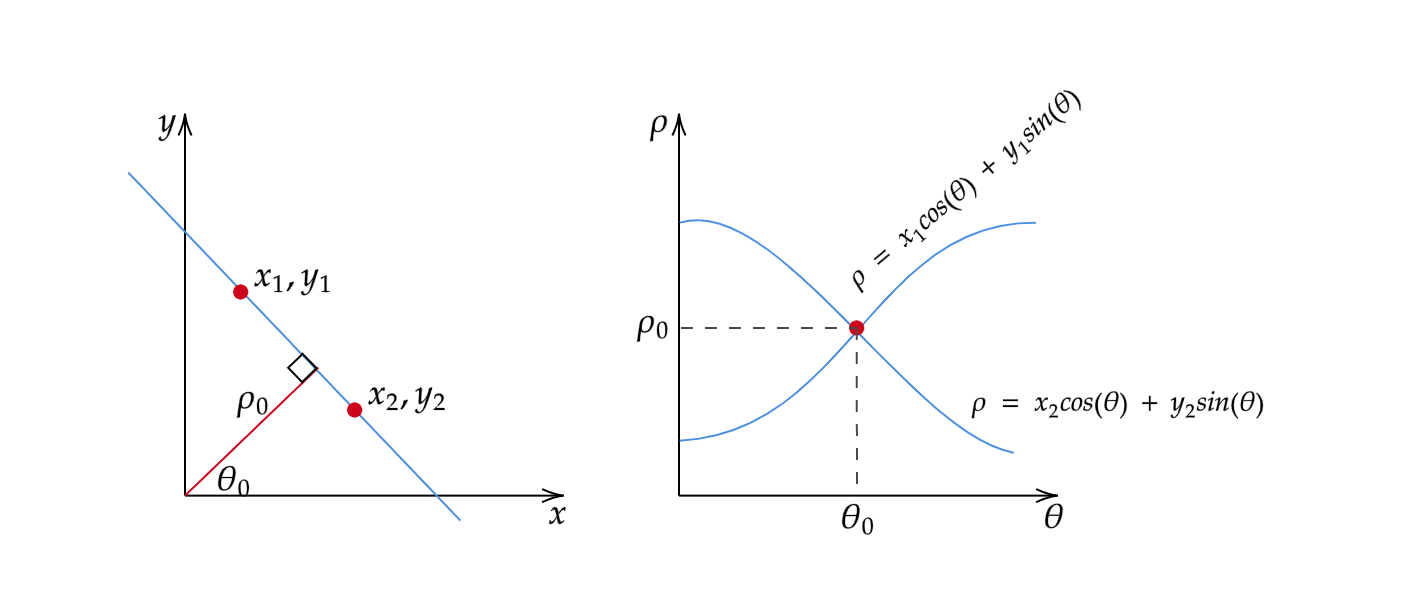
如下图，Q1，Q2，Q3,... ... 就是这些射线的原点的垂足点，在 $r-\theta$ 表格中表示成正弦曲线，

上图中的每一个P（x，y)决定一个圆，该圆在 $r-\theta$ 平面上对应一条三角曲线（下图）。如果有N个点构成直线，那么，就有N条三角曲线，且交于共同的一个点。

Lines Detection with Hough Transform | by Socret Lee | Towards Data Science

4.3 构建hough算法表格（在 $r-\theta$ 图）

1）构建在 $r-\theta$ 平面，用矩阵M表示,M初始值赋值为0

2）在图像中选取目标像素的坐标（x，y）

3）在 $\alpha \ \in [0,2\pi )$ 中取一个序列，从序列中选取一个 $\alpha$ 带入公式：

$r = xcos\cdot\alpha + y\cdot sin\alpha\: \: \: \: \:$

求出一个r。

4）刷新M矩阵，将对应的 $M(r,\alpha )$ 值加1.

5）循环完成后，M矩阵的每个峰值对应一条直线。

五、图像处理中，Hough变换如何应用

如果将图片中所有点参与直线提取，是不可取的，因此，需要边缘提取后，然后二值化处理，使得线上点数量规模减小后，用hough变换。

预处理图像，首先边缘提取
然后阈值二值化，将边缘点挑选出来备用。
对边缘点进行hough变换，生成M矩阵
选取M中峰值，将线条对应点提取出。

5.1 python程序代码

# coding=utf-8
import cv2
import numpy as npdef rgb2gray(rgb):return np.dot(rgb[..., :3], [0.299, 0.587, 0.114])Gray = cv2.imread("d:/images/lines1.jpg",0)height,width = Gray.shape
cv2.imshow("dsp",Gray)
cv2.waitKey(0)point ={}
num=0
for i in range(height):for j in range(width):if Gray[i][j] !=0:point[num]=[i,j]num+=1triTable ={}for i in range(180):triTable[i]=[np.sin(i*3.14159/180),np.cos(i*3.14159/180)]len_cross = int( np.sqrt( width**2+ height**2))
MtrScore = np.zeros([len_cross*2,180],np.int32)for i in range(num):ptmp = point[i]for j in range( 180 ):atmp = triTable[j]rou =int( ptmp[0]*atmp[0] + ptmp[1]*atmp[1] ) + len_cross# print(rou)MtrScore[rou][j] = MtrScore[rou][j]+ 1import seaborn as sns
import matplotlib.pyplot as plt
sns.heatmap( MtrScore )
plt.show()