【C++】2018华为软挑：模拟退火+贪心FF解决装箱问题

article/2025/9/15 15:51:55

本文的主要工作是补充这篇博客的缺失代码，使之能够运行。

2018华为软挑--模拟退火+FF解决装箱问题【C++代码】_小马哥MAX的博客-CSDN博客算法简介：        装箱问题是一个NP完全问题，求解全局最优解有很多种方法：遗传算法、禁忌搜索算法、蚁群算法、模拟退火算法等等，本次使用模拟退火，它的优点是在参数合适的情况下基本上可以100%得到全局最优解，缺点是相较于其他算法，其稳定速度较慢。        如果你对退火的物理意义还是晕晕的，没关系我们还有更为简单的理解方式。想象一下如果我们现在有下面这样一个函数，现在想求函数的（全局）最...https://blog.csdn.net/majichen95/article/details/80023320?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522165007496116780271530627%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=165007496116780271530627&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-80023320.nonecase&utm_term=%E6%A8%A1%E6%8B%9F%E9%80%80%E7%81%AB&spm=1018.2226.3001.4450

一、模拟退火算法介绍

          装箱问题是一个NP完全问题，求解全局最优解有很多种方法：遗传算法、禁忌搜索算法、蚁群算法、模拟退火算法等等，本次使用模拟退火，它的优点是在参数合适的情况下基本上可以100%得到全局最优解，缺点是相较于其他算法，其稳定速度较慢。

        如果你对退火的物理意义还是晕晕的，没关系我们还有更为简单的理解方式。想象一下如果我们现在有下面这样一个函数，现在想求函数的（全局）最优解。如果采用贪心策略，那么从A点开始试探，如果函数值继续减少，那么试探过程就会继续。而当到达点B时，显然我们的探求过程就结束了（因为无论朝哪个方向努力，结果只会越来越大）。最终我们只能找打一个局部最后解B。

         可以看出 模拟退火其实也是一种贪心算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以上图为例，模拟退火算法在搜索到局部最优解B后，会以一定的概率接受向右继续移动。也许经过几次这样的不是局部最优的移动后会到达B 和C之间的峰点，于是就跳出了局部最小值B。

算法过程：
        根据Metropolis准则，粒子在温度T时趋于平衡的概率为exp(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变数,k为Boltzmann常数。Metropolis准则常表示为

        Metropolis准则表明，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：P(dE) = exp( dE/(kT) )。其中k是一个常数，exp表示自然指数，且dE<0。所以P和T正相关。这条公式就表示：温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小。又由于dE总是小于0（因为退火的过程是温度逐渐下降的过程），因此dE/kT < 0 ，所以P(dE)的函数取值范围是(0,1) 。随着温度T的降低，P(dE)会逐渐降低。

        我们将一次向较差解的移动看做一次温度跳变过程，我们以概率P(dE)来接受这样的移动。也就是说，在用固体退火模拟组合优化问题，将内能E模拟为目标函数值 f，温度T演化成控制参数 t，即得到解组合优化问题的模拟退火演算法：由初始解 i 和控制参数初值 t 开始，对当前解重复“产生新解→计算目标函数差→接受或丢弃”的迭代，并逐步衰减 t 值，算法终止时的当前解即为所得近似最优解。

总结起来就是：
        若f( Y(i+1) ) <= f( Y(i) )  (即移动后得到更优解)，则总是接受该移动；
        若f( Y(i+1) ) > f( Y(i) )  (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）。相当于上图中，从B移向BC之间的小波峰时，每次右移（即接受一个更糟糕值）的概率在逐渐降低。如果这个坡特别长，那么很有可能最终我们并不会翻过这个坡。如果它不太长，这很有可能会翻过它，这取决于衰减 t 值的设定。

举个栗子

 求函数f(x)=11*sin(6*x)+7*cos(5*x) , x∈[0,2*pi] 的最小值。

 由函数图像可以看出函数fx的最小值是-17.833975，但存在很多极小值，要求全局最优可以采用模拟退火，具体代码如下：

//f(x)=11*sin(6*x)+7*cos(5*x),x∈[0,2*pi]，求最小值,真实最小值为-17.833  
#include <iostream>  
#include <math.h>  
#include <time.h>  #define pi 3.14159  
#define num 30000 //迭代次数  
double k = 0.01;
double r = 0.99; //用于控制降温的快慢  
double T = 200; //系统的温度，系统初始应该要处于一个高温的状态  
double T_min = 2;//温度的下限，若温度T达到T_min，则停止搜索  //返回指定范围内的随机浮点数  double rnd(double dbLow, double dbUpper)//产生（dbLow,dbUpper）之间的随机数
{double dbTemp = rand() / ((double)RAND_MAX + 1.0);return dbLow + dbTemp*(dbUpper - dbLow);
}double func(double x)//目标函数  
{return 11 * sin(6 * x) + 7 * cos(5 * x);
}int main()
{double best = func(rnd(0.0, 2 * pi));double dE, current;int i;srand((unsigned)(time(NULL)));//用当前时间点初始化随机种子，防止每次运行的结果都相同while (T > T_min){for (i = 0; i < num; i++){current = func(rnd(0.0, 2 * pi));//产生新解dE = current - best;if (dE < 0) //表达移动后得到更优解，则总是接受移动  best = current;else{// 函数exp( dE/T )的取值范围是(0,1) ，dE/T越大，则exp( dE/T )也越大  if (exp(-dE / (T*k)) > rnd(0.0, 1.0))//有一定概率接受较差解best = current;}}T = r * T;//降温退火 ，0<r<1 。r越大，降温越慢；r越小，降温越快  }printf("最小值是 %f\n", best);return 0;
}

 可以看出，模拟退火帮助我们得到了全局最优解。

二、装箱问题

        有n个物品，体积为v1，v2，v3. . .然后要求用最少的箱子把这些物品里面，这个是基于贪心算法的思想。

装箱问题_lotluck的博客-CSDN博客_装箱问题

三、华为软挑完整代码

题目：简单来说，就是有n个内存大小一样、CPU核数一样的大型物理机，作为装箱问题中的“箱子”，而用户需要的虚拟机是装箱问题中的“物品”，虚拟机根据用户的需求其内存大小、CPU核数是各不相同的。求最少需要几个大型物理机。

代码的分段讲解见这篇博客：2018华为软挑--模拟退火+FF解决装箱问题【C++代码】_小马哥MAX的博客-CSDN博客

不过该博主隐藏了数据结构和主程序调用，并且在函数部分做了一些“手脚”，使得程序没法运行。补充并修改完毕后，完整代码如下：

#include <iostream>  
#include <math.h>  
#include <time.h>  
#include <string>
using namespace std;int PsyPsNum = 0; //最优解，初始值无所谓，需要的物理机个数 
int totalPreNum = 15; //总虚拟机typedef struct Flavor{string s;  //服务器名称 int PsId;  //分配给了编号为PsId的云服务器 int cpu; //cpu大小 int mem; //存储大小 
}FlavorS; typedef struct GNode{    // 物品节点 int gnum;     // 挂在链上的编号 struct GNode *link;	 //指向下一个物品节点 
}GNode;typedef struct GBox{    // 物品节点 int remainder;     int mem;int box_no;struct GBox *next;	 //指向下一个物品节点 GNode *head;  //	  
}GBox;int FlavorSBox(FlavorS goods[], int n, int cpu_num, int mem);void distribution(FlavorS flavors[])
{//PsyPsNum = FlavorSBox(flavors, totalPreNum, ECS.cpu, ECS.mem);PsyPsNum = FlavorSBox(flavors, totalPreNum, 56, 128);
}int FlavorSBox(FlavorS goods[], int n, int cpu_num, int mem) //装箱问题贪心算法
{int num = 0;GNode *pg, *t;GBox *hbox = NULL, *pb, *qb;int i;for (i = 0; i < n; i++) //遍历虚拟机信息数组{pg = (GNode *)malloc(sizeof(GNode)); ///分配货物节点单元//pg->s = goods[i].s;pg->link = NULL; //货物节点初始化if (!hbox)		 //若一个物理服务器都没有{hbox = (GBox *)malloc(sizeof(GBox));hbox->remainder = cpu_num; //物理服务器可以容纳的CPUhbox->mem = mem;		   //物理服务器可以容纳的内存hbox->head = NULL;hbox->next = NULL;num++; //物理服务器数量加1hbox->box_no = num;}qb = pb = hbox; //都指向物理服务器头while (pb)		//找物理服务器{if (pb->remainder >= goods[i].cpu && pb->mem >= goods[i].mem) //CPU能装下&&内存也能装下 break;													  //找到箱子，跳出whileelse{qb = pb;pb = pb->next; //qb是前驱}} //遍历物理服务器结束if (pb == NULL) //需要新物理服务器{pb = (GBox *)malloc(sizeof(GBox)); //分配物理服务器pb->head = NULL;pb->next = NULL;pb->remainder = cpu_num;pb->mem = mem;qb->next = pb; //前驱指上num++;		   //物理服务器数量加1pb->box_no = num;}if (!pb->head) //如果物理服务器里没货{pb->head = pg;t = pb->head;goods[i].PsId = pb->box_no; //将虚拟机与物理服务器编号关联起来cout << goods[i].s << "装入" << goods[i].PsId << "物理服务器" << endl;}else{t = pb->head;while (t->link)t = t->link; //尾插t->link = pg;goods[i].PsId = pb->box_no; //将虚拟机与物理服务器编号关联起来cout << goods[i].s << "装入" << goods[i].PsId << "物理服务器" << endl;}pb->remainder -= goods[i].cpu;pb->mem -= goods[i].mem;}cout<<"需要服务器的个数"<<num<<endl; return num;
}//swapTimes表示交换次数，flavors表示需要交换的对象
void generateNew(int swapTimes, FlavorS flavors[])
{for (int i = 0; i < swapTimes; i++){int posx = rand() % totalPreNum;int posy = rand() % totalPreNum;swap(flavors[posx], flavors[posy]);}
}double rnd(double dbLow, double dbUpper)//产生（dbLow,dbUpper）之间的随机数
{double dbTemp = rand() / ((double)RAND_MAX + 1.0);return dbLow + dbTemp*(dbUpper - dbLow);
}void SimulatedFire(FlavorS flavors[])
{int best = PsyPsNum;cout << "before fire:" << PsyPsNum << endl;const int LL = 300;double k = 0.1;double r = 0.97;	 //用于控制降温的快慢double T = 300;		 //系统的温度，系统初始应该要处于一个高温的状态double T_min = 0.1; //温度的下限，若温度T达到T_min，则停止搜索//返回指定范围内的随机浮点数int dE, current;srand((unsigned)(time(NULL)));FlavorS *temp = new FlavorS[totalPreNum];for (int i = 0; i < totalPreNum; i++){temp[i].s = flavors[i].s;temp[i].cpu = flavors[i].cpu;temp[i].mem = flavors[i].mem;temp[i].PsId = flavors[i].PsId;}while (T > T_min){for (int i = 0; i < LL; i++){generateNew(50, temp);  //把15个箱子的顺序打乱 distribution(temp);  	//然后，重新利用贪心得到最小值 current = PsyPsNum;dE = current - best;if (dE <= 0) //表达移动后得到更优解，则总是接受移动{best = current;for (int i = 0; i < totalPreNum; i++){flavors[i].s = temp[i].s;flavors[i].cpu = temp[i].cpu;flavors[i].mem = temp[i].mem;flavors[i].PsId = temp[i].PsId;}}	else{// 函数exp( dE/T )的取值范围是(0,1) ，dE/T越大，则exp( dE/T )也越大if (exp(-dE / (T * k)) > rnd(0.0, 1.0)){best = current;for (int i = 0; i < totalPreNum; i++){flavors[i].s = temp[i].s;flavors[i].cpu = temp[i].cpu;flavors[i].mem = temp[i].mem;flavors[i].PsId = temp[i].PsId;}}}}T = r * T; //降温退火 ，0<r<1 。r越大，降温越慢；r越小，降温越快}PsyPsNum = best;delete[] temp;cout << "after fire:" << PsyPsNum << endl;
}int main(){
//	int N;  //输入多少个服务器
//	scanf("%d",&N);
//	
//	FlavorS flavors[N];
//	for(int i=0;i<N;i++){
//		scanf("%s %d %d",&flavors[i].s;&flavors[i].cpu,&flavors[i].mem);
//	} int N=15;FlavorS flavors[15];/*---------------内存的单位是mb---------------*/
//	flavors[0].s="flavor14"; flavors[0].cpu=16; flavors[0].mem=32768;
//	flavors[1].s="flavor11"; flavors[1].cpu=8; flavors[1].mem=16384;
//	flavors[2].s="flavor9"; flavors[2].cpu=4; flavors[2].mem=16384;
//	flavors[3].s="flavor8"; flavors[3].cpu=4; flavors[3].mem=8192;
//	flavors[4].s="flavor6"; flavors[4].cpu=2; flavors[4].mem=8192;
//	flavors[5].s="flavor5"; flavors[5].cpu=2; flavors[5].mem=4096;
//	flavors[6].s="flavor4"; flavors[6].cpu=2; flavors[6].mem=2048;
//	flavors[7].s="flavor3"; flavors[7].cpu=1; flavors[7].mem=4096;
//	flavors[8].s="flavor2"; flavors[8].cpu=1; flavors[8].mem=2048;
//	flavors[9].s="flavor1"; flavors[9].cpu=1; flavors[9].mem=1024;
//	flavors[10].s="flavor7"; flavors[10].cpu=4; flavors[10].mem=4096;
//	flavors[11].s="flavor10"; flavors[11].cpu=8; flavors[11].mem=8192;
//	flavors[12].s="flavor12"; flavors[12].cpu=8; flavors[12].mem=32768;
//	flavors[13].s="flavor13"; flavors[13].cpu=16; flavors[13].mem=16384;
//	flavors[14].s="flavor15"; flavors[14].cpu=16; flavors[14].mem=65536;/*---------------内存的单位是GB---------------*/flavors[0].s="flavor14"; flavors[0].cpu=16; flavors[0].mem=32768/1024;flavors[1].s="flavor11"; flavors[1].cpu=8; flavors[1].mem=16384/1024;flavors[2].s="flavor9"; flavors[2].cpu=56; flavors[2].mem=16384/1024;flavors[3].s="flavor8"; flavors[3].cpu=56; flavors[3].mem=8192/1024;flavors[4].s="flavor6"; flavors[4].cpu=56; flavors[4].mem=8192/1024;flavors[5].s="flavor5"; flavors[5].cpu=56; flavors[5].mem=4096/1024;flavors[6].s="flavor4"; flavors[6].cpu=56; flavors[6].mem=2048/1024;flavors[7].s="flavor3"; flavors[7].cpu=56; flavors[7].mem=4096/1024;flavors[8].s="flavor2"; flavors[8].cpu=56; flavors[8].mem=2048/1024;flavors[9].s="flavor1"; flavors[9].cpu=1; flavors[9].mem=1024/1024;flavors[10].s="flavor7"; flavors[10].cpu=4; flavors[10].mem=4096/1024;flavors[11].s="flavor10"; flavors[11].cpu=8; flavors[11].mem=8192/1024;flavors[12].s="flavor12"; flavors[12].cpu=8; flavors[12].mem=32768/1024;flavors[13].s="flavor13"; flavors[13].cpu=16; flavors[13].mem=16384/1024;flavors[14].s="flavor15"; flavors[14].cpu=16; flavors[14].mem=65536/1024;distribution(flavors);  //得到贪心算法的最优解，放入PsyPsNum中 SimulatedFire(flavors); return 0;
}

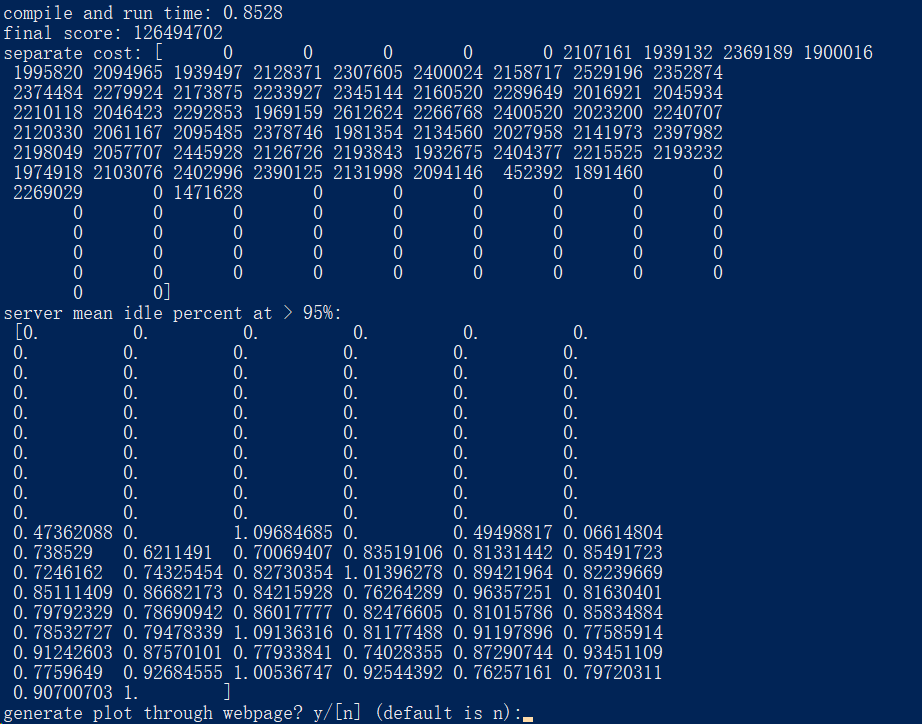
要想理解这个程序的输入和输出必须找华为软挑初赛的原题看一下！

跑完这个大概需要1~2分钟时间，耐心等待。


http://chatgpt.dhexx.cn/article/ZxBwD7cy.shtml

相关文章

2020华为软挑热身赛-这些坑我帮你踩过了（华为软件精英挑战赛编程闯关）

2020华为软挑热身赛-这些坑我帮你踩过了（华为软件精英挑战赛编程闯关）

本文始发于个人公众号【两猿社】。 声明&#xff0c;为保证比赛公平&#xff0c;本文不会提供比赛源码&#xff0c;仅提供思路与踩坑经验。 他来了&#xff0c;他来了&#xff0c;他带着面试绿卡走来了。 他来了&#xff0c;他来了&#xff0c;他带着20w大奖走来了。 一年一度…
阅读更多...
2018华为软挑参赛体验

2018华为软挑参赛体验

第一次接触到这个比赛应该是研究生刚入学的时候&#xff0c;在教研室看到了师姐的一份简历&#xff0c;上面就有华为软挑的参赛经历。研一利用空余时间加强C和STL的学习&#xff0c;看完了《C primer》《Effective STL》&#xff0c;自己也写了一些demo&#xff0c;感觉这个比赛…
阅读更多...
2022华为软挑编程问题报错总结

2022华为软挑编程问题报错总结

for i in number_feature: TypeError: ‘int’ object is not iterable的错误 错误原因&#xff1a;是因为在python里&#xff0c;整型&#xff08;int&#xff09;数据是不能直接用于迭代的&#xff0c;而是应该用range()函数 改为如下图&#xff1a;
阅读更多...
2021华为软挑部分答疑——哪些你有错却总是找不到的地方，我来带你找啦（含标准输入代码）

2021华为软挑部分答疑——哪些你有错却总是找不到的地方，我来带你找啦（含标准输入代码）

前期工作&#xff1a; 2021华为软挑初探——代码实现 2021华为软挑再探——代码实现 1 关于打包 在windows系统下&#xff0c;先把你写的程序写在src里面的CodeCraft-2021里面 然后在这个页面&#xff0c;将这三个文件压缩就可以上传啦&#xff1a; 2 关于标准输入 标准输…
阅读更多...
华为软挑2019

华为软挑2019

参加软挑的一些感悟 写在前边的话 我本科一直在做嵌入式相关的项目,这是第一次参加软件类的竞赛,不得不说过程确实很刺激,最后止步杭厦赛区50强也很是遗憾,明明很接近,最后输在了代码效率上,本地成绩很好的 python代码 ,上传测评运行时间超限&#xff08;官测环境比本地性能好&…
阅读更多...
2021华为软挑初探——代码实现

2021华为软挑初探——代码实现

其他工作&#xff1a; 2021华为软挑部分答疑——哪些你有错却总是找不到的地方&#xff0c;我来带你找啦&#xff08;含标准输入代码&#xff09; 2021华为软挑再探——代码实现 这几天华为软挑好多人也是做的热火朝天&#xff0c;作为一个渣渣小孙也来探探&#xff0c;不探…
阅读更多...
2020华为软挑总结

2020华为软挑总结

文章目录 一、热身赛编程闯关&#xff1a;评价标准&#xff1a;问题分析 二、初赛问题描述评价标准&#xff1a;问题分析思路一&#xff1a;思路二&#xff1a;思路三&#xff1a;针对思路三的提速&#xff1a; 最终结果&#xff1a; 三、code记录初赛两篇不错的总结三、复活赛…
阅读更多...
2022华为软挑比赛（初赛笔记）

2022华为软挑比赛（初赛笔记）

文章目录 2022华为软挑&#xff08;初赛笔记&#xff09;1. 赛题要求2. 解决方案2.1 挑选适合的边缘节点2.2 第一轮&#xff1a;最大分配2.3 第二轮&#xff1a;均值分配 总结 本文仓库地址&#xff1a; Github-CodeCraft-2022 2022华为软挑&#xff08;初赛笔记&#xff09; …
阅读更多...
2023华为软件精英挑战赛笔记心得（Python实现）

2023华为软件精英挑战赛笔记心得（Python实现）

第一次参加华为软挑&#xff0c;问了周围一圈人没人组队&#xff0c;看了眼题目&#xff0c;感觉挺有意思的&#xff0c;就打算自己写来跑一下&#xff0c;不求分数&#xff0c;主要是想学点东西&#xff0c;顺便记录一下。&#xff08;最后跑了195w&#xff0c;自己的能力也就…
阅读更多...
2021华为软件精英挑战总结

2021华为软件精英挑战总结

2021华为软挑32强总结 今年的软挑最终止步于粤港澳赛区第16名&#xff0c;总成本为16亿3979万6349&#xff0c;赛区第一名总成本为15亿3903万4817。 虽然没进入决赛&#xff0c;但是拿到了华为面试直通卡&#xff0c;也喜提广州一日游&#xff0c;算不虚此行了。决赛虽然还在继…
阅读更多...
Spring认证中国教育管理中心-Spring Data Neo4j教程一

Spring认证中国教育管理中心-Spring Data Neo4j教程一

原标题&#xff1a;Spring认证中国教育管理中心-Spring Data Neo4j教程一&#xff08;Spring中国教育管理中心&#xff09; 5. 开始 我们为 SDN 提供了 Spring Boot 启动器。请通过您的依赖管理包含启动模块并配置要使用的螺栓 URL&#xff0c;例如org.neo4j.driver.uribolt:/…
阅读更多...
SpringBoot 整合 Neo4j

SpringBoot 整合 Neo4j

1、创建测试类2、集成 SpringBoot 阅读此文之前&#xff0c;必须对 Neo4j 有个初步的了解&#xff0c;如果要实际操作的话&#xff0c;需要自备一个 Neo4j 数据库 本文所涉及代码已开源至 Gitee https://gitee.com/Array_Xiang/spring-boot-neo4j 创建一个 SpringBoot 项目&…
阅读更多...
【Neo4j教程之CQL函数基本使用】

【Neo4j教程之CQL函数基本使用】

&#x1f680; Neo4j &#x1f680; &#x1f332; 算法刷题专栏 | 面试必备算法 | 面试高频算法 &#x1f340; &#x1f332; 越难的东西,越要努力坚持&#xff0c;因为它具有很高的价值&#xff0c;算法就是这样✨ &#x1f332; 作者简介&#xff1a;硕风和炜&#xff0c;C…
阅读更多...
Neo4j资料 Neo4j教程 Neo4j视频教程 Neo4j 图数据库视频教程

Neo4j资料 Neo4j教程 Neo4j视频教程 Neo4j 图数据库视频教程

课程发布地址 地址&#xff1a; 腾讯课堂《Neo4j 图数据库视频教程》 https://ke.qq.com/course/327374?tuin442d3e14 作者 庞国明&#xff0c;《Neo4j权威指南》副主编、《Neo4j 3.x 入门经典》翻译 邮箱&#xff1a;pangguomingyeah.netQQ:1143815700Neo4j技术讨论QQ群&…
阅读更多...
Neo4J超详细专题教程，快来收藏起来吧

Neo4J超详细专题教程，快来收藏起来吧

Neo4J超详细教程 Lecture&#xff1a;波哥 一、Neo4J相关介绍 1.为什么需要图数据库 随着社交、电商、金融、零售、物联网等行业的快速发展&#xff0c;现实社会织起了了一张庞大而复杂的关系 网&#xff0c;传统数据库很难处理关系运算。大数据行业需要处理的数据之间的关系随…
阅读更多...
Neo4j教程 Neo4j视频教程 Neo4j 图数据库视频教程

Neo4j教程 Neo4j视频教程 Neo4j 图数据库视频教程

课程发布地址 地址&#xff1a; 腾讯课堂《Neo4j 图数据库视频教程》 https://ke.qq.com/course/327374?tuin442d3e14 作者 庞国明&#xff0c;《Neo4j权威指南》副主编、《Neo4j 3.x 入门经典》翻译 邮箱&#xff1a;pangguomingyeah.netQQ:1143815700Neo4j技术讨论QQ群&…
阅读更多...
neo4j教程-安装部署

neo4j教程-安装部署

neo4j教程-安装部署 Neo4j的关键概念和特点 •Neo4j是一个开源的NoSQL图形存储数据库&#xff0c;可为应用程序提供支持ACID的后端。Neo4j的开发始于2003年&#xff0c;自2007年转变为开源图形数据库模型。程序员使用的是路由器和关系的灵活网络结构&#xff0c;而不是静态表…
阅读更多...
Neo4j安装教程

Neo4j安装教程

1.下载社区版本&#xff0c;java8推荐安装3.*的版本 Neo4j Download Center - Neo4j Graph Data Platformhttps://neo4j.com/download-center/#community 点击下载即可。 2.配置 启动 将提取的文件放在服务器上的永久主页中&#xff0c;例如 D:\neo4j\. 顶级目录称为 NEO4J_…
阅读更多...
Neo4j详细介绍及使用教程

Neo4j详细介绍及使用教程

文章目录 一、Neo4j介绍1.Neo4j简介2.图数据库简介3.Neo4j的优缺点4.Neo4j的常见应用场景二、使用教程1.下载安装2.数据插入和查询(1)基本概念(2)基本语法Ⅰ.CREATE操作——创建Ⅱ.MERGE——创建或更新Ⅲ.Match操作——查找指定的图数据Ⅳ.DELETE操作——删除节点3.JAVA实战 一…
阅读更多...
Neo4j语法教程

Neo4j语法教程

neo4j简版教程 create (<node-name:<label-name2>:<label-name2>......>) return <node-name> 可以给一个节点创建多label的node eg: CREATE (dept:Dept { deptno:10,dname:"Accounting",location:"Hyderabad" }) Neo4j CQL创…
阅读更多...
推荐文章

Copyright @ 2022~2023