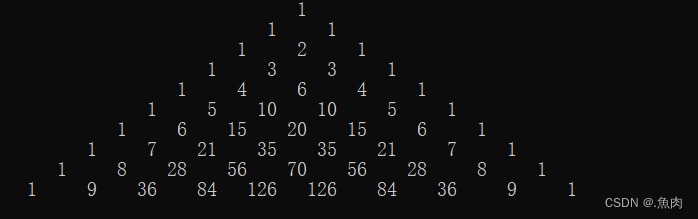
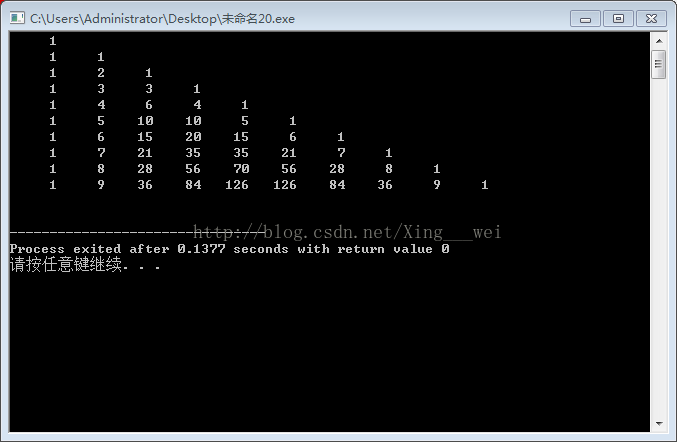
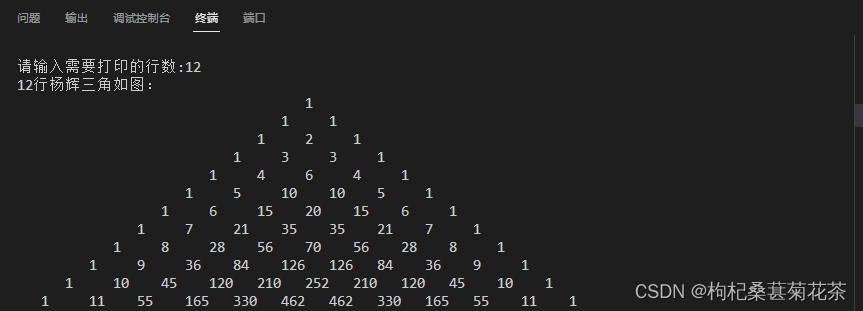
下面为大家介绍用二维数组来输出任意行的杨辉三角。有以下步骤:
1:利用一个全局变量来控制数组,从而控制杨辉三角大小。
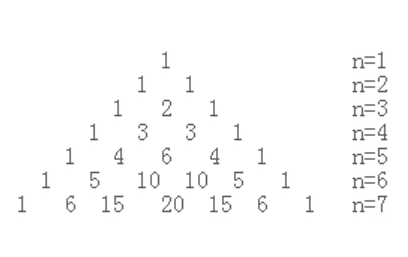
2:分别用for循环进行对杨辉三角进行赋值。(利用它每个数等于它上方两个数和的规律)
3:控制格式进行输出。
int a[100][100]; //创建一个全局变量来控制数组大小
int main()
{int i = 0, j = 0, k, n;scanf("%d", &n);for (i = 0; i < n; i++){a[i][0] = 1; //先把左右两边的1赋值完a[i][j] = 1;j += 1;}for (i = 2; i < n; i++) //用来把杨辉三角各个值进行赋值 for (j = 1; j <= i - 1; j++)a[i][j] = a[i - 1][j - 1] + a[i - 1][j];k = 2 * n - 2;for (i = 0; i < n; i++){if (k >= 0){while (k >= 0){k -= 1;printf(" ");//完善杨辉三角格式}for (j = 0; j <= i; j++){printf("%-4d", a[i][j]);}printf("\n");k = 2 * n - i * 2 - 4;//每换行一次,下一行的1就往前移4格 } //所以在于原有基础上-4 } //因为1我用的是-4%d。return 0;
}输入行数,输出如下:

这是输出10行的杨辉三角:
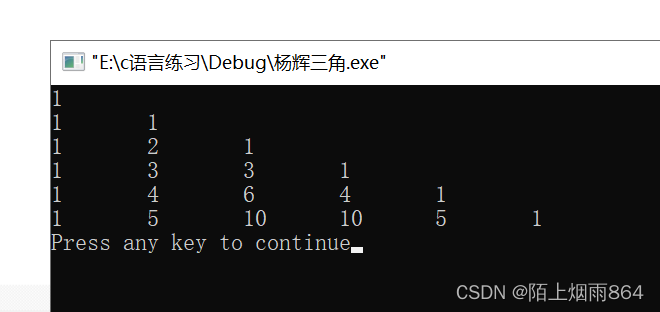
#include <stdio.h>
int main()
{int i=0, j=0, a[10][11],k;for (i = 0; i < 10; i++){a[i][0] = 1;a[i][j] = 1;j += 1;}for (i = 2; i < 10; i++)for (j = 1; j <= i - 1; j++)a[i][j] = a[i - 1][j - 1] + a[i - 1][j]; k = 19;for (i = 0; i < 10; i++){if (k >= 0){while (k > 0){k -= 2;printf(" ");}for (j = 0; j <= i; j++){printf("%-4d", a[i][j]);}printf("\n");k = 17 - i * 2;}}return 0;
}
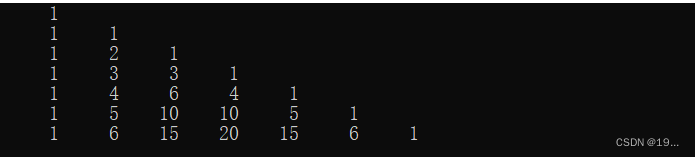

![[C语言]杨辉三角形:编程计算并输出打印前n行杨辉三角形。请使用数组实现。](https://img-blog.csdnimg.cn/3004bf0f03914875be045e1034c48990.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAX0NoaWNrZW5f,size_15,color_FFFFFF,t_70,g_se,x_16)