要求：
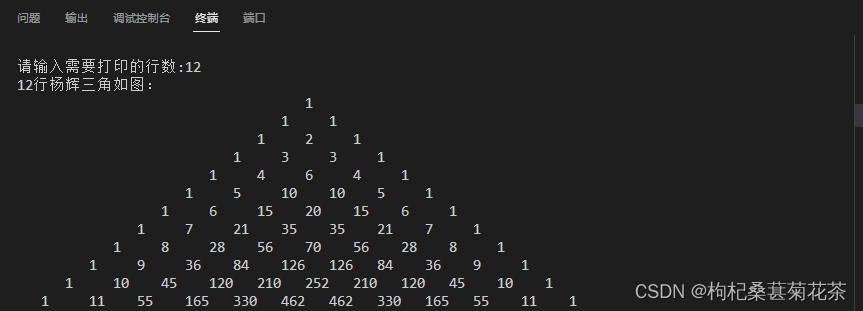
输出以下的杨辉三角形（要求输出10行）（12分）
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10  5 1
: : : : : :

方法1:

#include<stdio.h>#define  row 10
#define  col 10int main () {int  i,j;int arr[row][col];for(i=0;i< row ;i++) {     //初始化 每行第一个和最后一个元素值都为1arr[i][i] = 1;arr[i][0] = 1;}for(i = 2;i<row;i++){    //从第三行开始for(j = 1;j<i;j++) {arr[i][j]=arr[i-1][j-1]+arr[i-1][j]; //每个数等于它上方两数之和。}}for(i = 0;i<row;i++){for(j = 0;j<=i;j++) {printf("%5d",arr[i][j]);}printf("\n");}return 0;}

直接说上面的思路：
对于这种杨辉三角，每一行的第一个元素和每一行的最后一行元素都是1，而且其实从第2行就开始有的一个规律就是：“从第二列开始，每个位置元素的值等于上一行元素前一列的值和上一行元素同一列的值之和。”，自然而言我们就想到了使用二维数组。

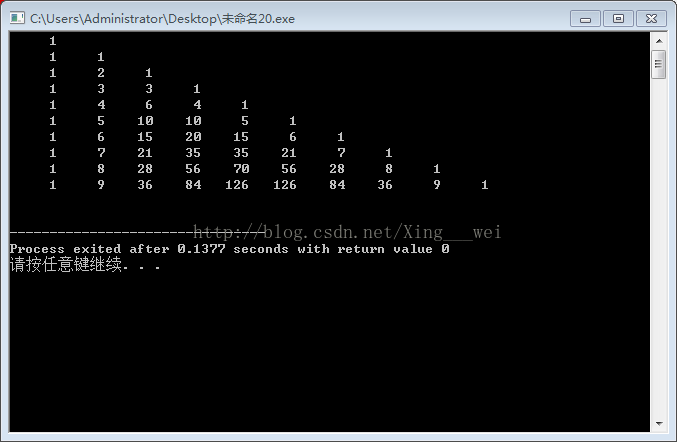
输出结果：

方法2:

#include<stdio.h>#define  row 10
#define  col 10int main () {int  i,j;int arr[row][col]={};for(i = 0;i<row;i++){    //从第三行开始arr[i][0] = 1;for(j = 1;j<=i;j++) {arr[i][j]=arr[i-1][j-1]+arr[i-1][j]; //每个数等于它上方两数之和。}}for(i = 0;i<row;i++){for(j = 0;j<=i;j++) {printf("%5d",arr[i][j]);}printf("\n");}return 0;}

刚刚我们说了每一行的最后一个元素也是符合规律的，所以方法一种的arr[i][i] = 1;就没有必要写了，然后 arr[i][0] = 1;又可以放在下面的循环中，所以直接省去了一个循环，在效率上得到了很强的提升。注意，那么<此时二维数组的定义的格式：int arr[row][col]={};而不能是int arr[row][col];，因为加上{}就相当于有了数组的初始化，数组中所有的元素都是0而已，如果不加{}就相当于没有初始化，数组中的值都不确定，所以对于求每一行最后一个值的时候就开始出错。/font>

方法3:

使用一维数组也是可以的：

#include<stdio.h>
int main()
{ int i,j,n=0,a[17]={0,1},l,r;while(n<1 || n>16){printf("请输入杨辉三角形的行数:");scanf("%d",&n);}for(i=1;i<=n;i++){l=0;for(j=1;j<=i;j++){r=a[j];a[j]=l+r;   /*每个数是上面两数之和*/l=r;printf("%5d",a[j]);   /*输出杨辉三角*/}printf("\n");}
}