前言

菜鸡树木出的新密码题，质量不高，大佬们不要喷呜呜呜

题目信息

题目名称：No Ciphertext RSA

题目作者：树木有点绿

描　　述: The ciphertext is unknown!

解题过程

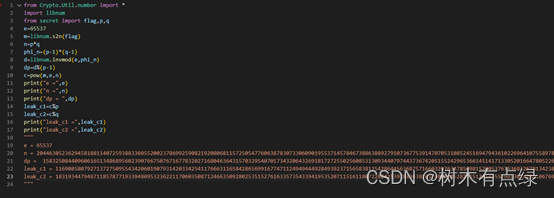
通过观察发现题目给了dp，那么我们可以根据dp推出p，然后根据n与pq的关系求出q

e = 65537
n = 20446305236294581881140725938833605520023786992590821920806811572505477606387830733060901955371457846738863889279107367753914707053108524516947943610226964107558978693717655472431318403586269727573489946433389159145602800207787382180423611018458189828931572992863289292613405218278949739073786959411566919119158325510346523951336418479951932209799501108477995314359188860274532542630968951457343647522078553891223764285682602714616115281040492374167771746275218863543545907073818468841626731849010162645256595641473022327747346052186526727216525426337190917106751151745388854749923598231196090790074682287345100965373
dp =  158325084409606165134868956023907667507671677832027168046364315703295407017343206432691817272550256085313093440797443736742051552429653661451417133052016647805226890534559578502154540190596419643135611407218228612201386225040438407799879719366484669372051153511312310009858718254183049095347658106745575535469
for i in range(1,65535):p=(dp*e-1)//i+1if n%p==0:break
print(p)
#176880281220421384276770426697672033095535078075714508749353553548240276323610202856692980610806418687790464096511235044404620241239340834109671075804268777866611345077962413424290036147269400193518437230146620445225908578474569771436035545465911591432888691958522976733082929634591293998871492096106249085747

然后我们使用q=n//p求出q

n=20446305236294581881140725938833605520023786992590821920806811572505477606387830733060901955371457846738863889279107367753914707053108524516947943610226964107558978693717655472431318403586269727573489946433389159145602800207787382180423611018458189828931572992863289292613405218278949739073786959411566919119158325510346523951336418479951932209799501108477995314359188860274532542630968951457343647522078553891223764285682602714616115281040492374167771746275218863543545907073818468841626731849010162645256595641473022327747346052186526727216525426337190917106751151745388854749923598231196090790074682287345100965373
p=176880281220421384276770426697672033095535078075714508749353553548240276323610202856692980610806418687790464096511235044404620241239340834109671075804268777866611345077962413424290036147269400193518437230146620445225908578474569771436035545465911591432888691958522976733082929634591293998871492096106249085747
q=n//p
print(q)
#115594033971571906870674970630915982265473520658575817480573873228902478910162856689799762790434945040173985337386002280961456435302076145225402559274043951375941233922060296662348241974538390649557790352060766898957619823324331799986614029809180092244051635825912380759159031412761681296336889781840027922959

紧接着，我们发现题目还给了leak_c1和leak_c2

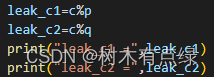
但是题目并没有给出密文c，所以推测是要我们根据这两个已知信息求解c

这里我们用到了中国剩余定理（CRT），即p和q是互相独立的大素数，n为p*q，对于任意(m1, m2), (0<=m1< p, 0<=m2< p)，这里把m1和m2替换成leak_c1和leak_c2，即可得到以下关系，我们发现这个关系完全符合以上定理

leak_c1 = c mod p
leak_c2 = c mod q

然后按照参考资料中的额Using the CTR with RSA即可根据leak_c1和leak_c2求解出c了

import gmpy2
p=115594033971571906870674970630915982265473520658575817480573873228902478910162856689799762790434945040173985337386002280961456435302076145225402559274043951375941233922060296662348241974538390649557790352060766898957619823324331799986614029809180092244051635825912380759159031412761681296336889781840027922959
q=176880281220421384276770426697672033095535078075714508749353553548240276323610202856692980610806418687790464096511235044404620241239340834109671075804268777866611345077962413424290036147269400193518437230146620445225908578474569771436035545465911591432888691958522976733082929634591293998871492096106249085747
c_mod_p=116908580792713727509554342060190793142033425411766631165842865699167747112494944492849392371565838125428644563687571660329763478509815200537676368326781342382868082294015200439334832938068779547847851748337854603115134732593759473453640093195977206450633212921689957303431235603192670553553803757864481012599
c_mod_q=18319344794671185787719339480953236221170603508712466350928025351527616335735433941953520711516118072282425397883638101260674452825151245435529613074796106769481242318321469286177813223159476396555044378245229663195991557031227024085316255781963813911437991309663376270820486723382786632243229800891705679245
e=65537
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
def CRT(aList, mList):M = 1for i in mList:M = M * ix = 0for i in range(len(mList)):Mi = M // mList[i]Mi_inverse = gmpy2.invert(Mi, mList[i])x += aList[i] * Mi * Mi_inversex = x % Mreturn x
if __name__ == "__main__":cList = [c_mod_p,c_mod_q]nList = [p,q]c = CRT(cList, nList)print(c)
#881223005013212329516680779770112213932184717575593705059275649183771089334628141202161640442530077373534574194323145344622196586510840109564222578976180247878668441243862824751264767688497192099460387965900121726924892410031343711180815011769897015729229501184255927235055838507628915398431057531348154667508394459894331052112012032490537515446990471398370280340641701058186108963013790688209990817631026484000900586136761003829319887875321641336302671586230087977190633848648706216633068142114296047157075398888299015627324219218846601055728510906015989112340983567350225119500049135045815437014263719857972698084

完整代码如下：

import gmpy2
from Crypto.Util.number import *
e = 65537
n = 20446305236294581881140725938833605520023786992590821920806811572505477606387830733060901955371457846738863889279107367753914707053108524516947943610226964107558978693717655472431318403586269727573489946433389159145602800207787382180423611018458189828931572992863289292613405218278949739073786959411566919119158325510346523951336418479951932209799501108477995314359188860274532542630968951457343647522078553891223764285682602714616115281040492374167771746275218863543545907073818468841626731849010162645256595641473022327747346052186526727216525426337190917106751151745388854749923598231196090790074682287345100965373
dp =  158325084409606165134868956023907667507671677832027168046364315703295407017343206432691817272550256085313093440797443736742051552429653661451417133052016647805226890534559578502154540190596419643135611407218228612201386225040438407799879719366484669372051153511312310009858718254183049095347658106745575535469
for i in range(1,65535):p=(dp*e-1)//i+1if n%p==0:q=n//pbreak
c_mod_p = 116908580792713727509554342060190793142033425411766631165842865699167747112494944492849392371565838125428644563687571660329763478509815200537676368326781342382868082294015200439334832938068779547847851748337854603115134732593759473453640093195977206450633212921689957303431235603192670553553803757864481012599
c_mod_q = 18319344794671185787719339480953236221170603508712466350928025351527616335735433941953520711516118072282425397883638101260674452825151245435529613074796106769481242318321469286177813223159476396555044378245229663195991557031227024085316255781963813911437991309663376270820486723382786632243229800891705679245
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
def CRT(aList, mList):M = 1for i in mList:M = M * ix = 0for i in range(len(mList)):Mi = M // mList[i]Mi_inverse = gmpy2.invert(Mi, mList[i])x += aList[i] * Mi * Mi_inversex = x % Mreturn x
if __name__ == "__main__":cList = [c_mod_p,c_mod_q]nList = [p,q]c = CRT(cList, nList)m=pow(c,d,n)print(long_to_bytes(m))