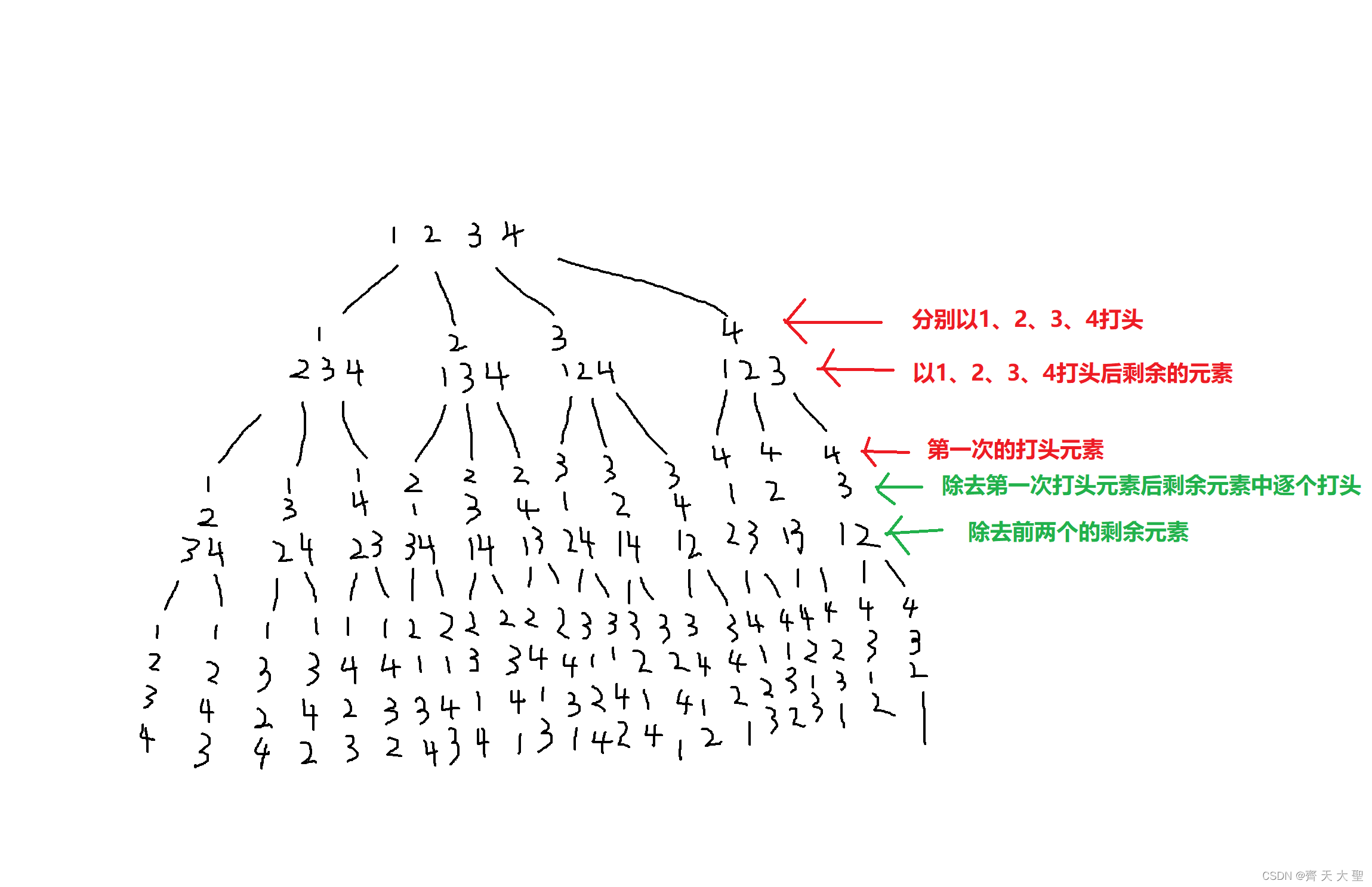
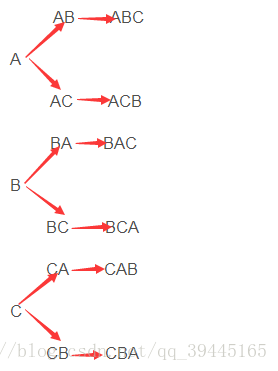
全排列

给定N个数，如 [1,2,3,4,5]，获取它的全排列

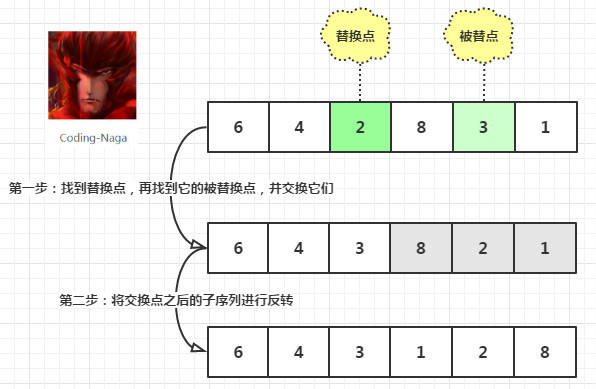
经典交换算法

核心思路是交换

#include<stdio.h>
void swap(int* a, int* b){int temp = *a;*a = *b;*b = temp;
}
//int a[] = { 1,2,3,4};
//sort(a, 0, 4);	
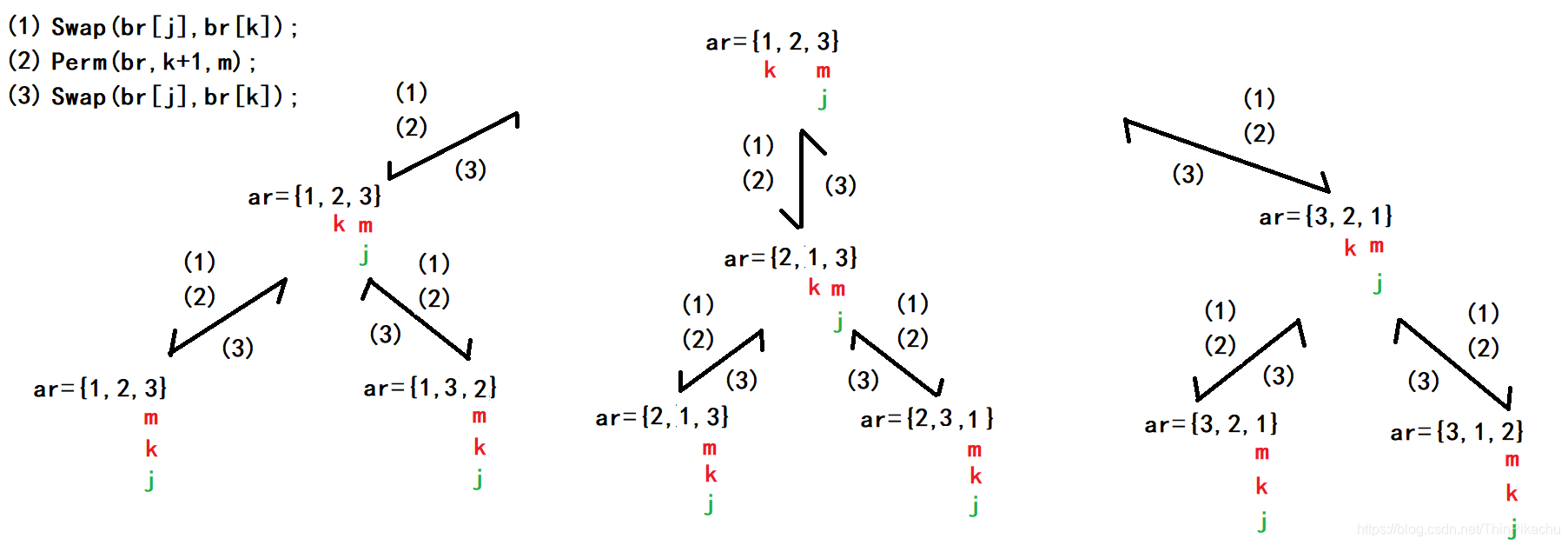
void sort(int* a, int k, int m){if (k == m){int i = 0; for (; i < m; i++){printf("%d", a[i]);}}else{int j = k;for (; j < m; j++){swap(&a[k], &a[j]);		sort(a, k + 1, m);swap(&a[k], &a[j]);}printf("\n");}
} // 上述代码的js版本
let arr = [1, 2, 3, 4];
let res = []
function sort(arr, k) {if (k === arr.length) return res.push(arr);for (let a = k; a < arr.length; a++) {let arr1 = [...arr];let t = arr1[k];arr1[k] = arr1[a];arr1[a] = t;sort(arr1, k + 1)}
}
sort(arr, 0, 4);
console.log(res)

动态规划 DP

有图有真相，把每次方法的返回值作为数组一部分递归调用。
排列算法

  function dp(arr) {if (arr.length === 1) {return arr;}let r = [];for (let a = 0; a < arr.length; a++) {let arr1 = [...arr];let v = arr1[a];arr1.splice(a, 1);dp(arr1).forEach(e => {let t = []t = t.concat(e, v)r.push(t)})}return r;}

元素移动

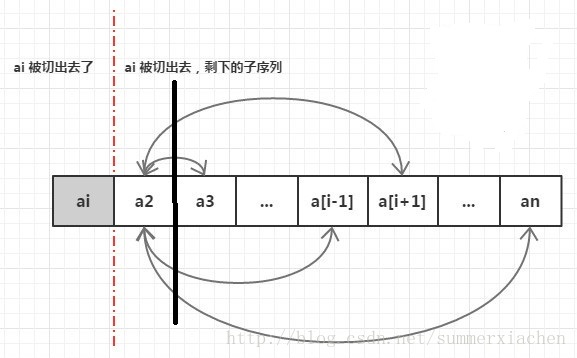
定义两个数组，源数组和目标数组，从源不停的往目标移动，源空了
就代表生成了一个排列。

  // 全排列，移动算法 从源数组不停的向目标数组移动，直到源数组拿空function range(list) {let r = [];function move(src, dist) {if (!src.length) {return r.push(dist)}src.forEach((v, i) => {// 复制一份源数组，删除第i个let s = [...src];s.splice(i, 1)// 把第i个放到目标数组中let d = [...dist, v]move(s, d)})}move(list, [])return r;}