写在前面

很久很久以前就想写的一篇博客，因为懒一直没开工，但是学习全排列算法算是我对递归理解的转折点，感觉很有意义，后来发现全排列、组合、求子集这三个算法在形式或理解上都有很多相似点，而我比较喜欢把相似的东西放在一起，这样才能更加深入地理解而又不混淆，因此接下来我会把这三个算法分三个博客都写一下。
全排列：本文
组合：组合算法
求子集：求子集算法

全排列

全排列有两种形式：一种是无重复数字全排列，一种是有重复数字全排列，这两种情况的处理方式有一些细微的差别，这一点会在后面作解释。

1 无重复数字全排列

leetcode实战：全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

1.1 紫书版本

第一次学习这个算法是看的刘汝佳老师的紫书，这篇博客的思路部分会按照紫书的思路来，后面的回溯法是我学习了八皇后回溯算法之后自己理解的，个人感觉回溯法更好理解。
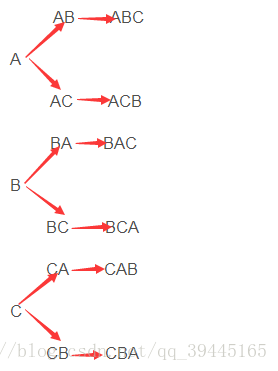
紫书版本采用递归寻找nums数组的全排列，函数permutation(pos,lens,nums,cur)的意思是从nums数组里选择一个数字放入cur[pos]中，使得cur[0…pos]中无重复数字，因此每次在为cur[pos]选数字的时，都需要遍历cur[0…pos-1]，当选择的数字不在里面时，就可以让cur[pos]=选择的数字，如果已经存在，则继续尝试下一个数字。尝试的过程就是对nums数组的遍历，因为是全排列，因此每一位都一定能找到一个数字。
找到所有全排列的关键是cur中每个位置，都需要通过遍历nums数组，即nums数组中的每个数字都会被放在cur中的每个位置上，因此加上不能重复的限制，就可以找到一组数字的所有全排列。
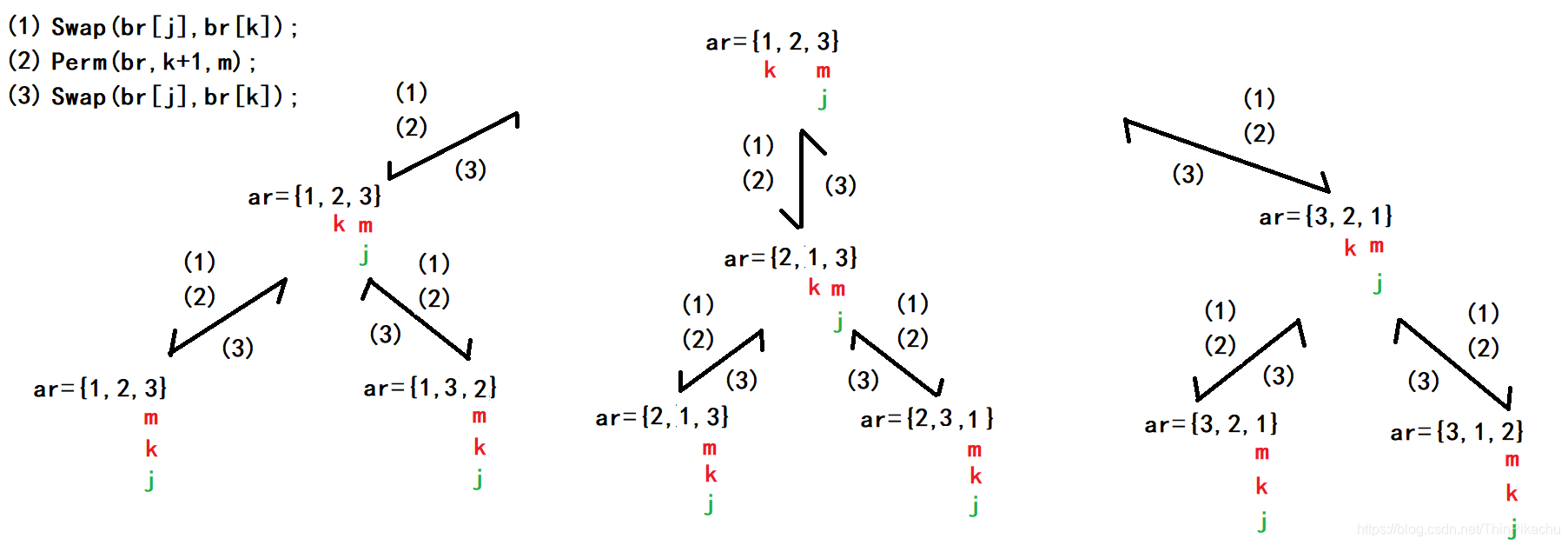
下面用一张图展示找到一个全排列的过程：

当找到一个全排列以后，会退回上一个递归程序中继续寻找，寻找流程如下：（结合图一起理解）

1. 当执行到pos=lens层时，会记录下这个全排列，然后返回上一层，即为cur[lens-1]选择数字;
2. 返回到pos=lens-1层，本来在pos=lens-1层选择了4，它已经被记录了下来，因此程序会继续选数字，但是发现在当前子程序中，除了4已经没有其他选择，因此再次返回上一层，即为cur[lens-2]选数字;
3. 返回到pos=lens-2层,此时相当于已经确定了[1,5,2,6]，程序会为cur[lens-2]选择除了7以外的数字，发现4可行，然后将4放入cur[pos-2]中，cur[0…pos]=[1,5,2,6,4]，继续递归pos+1层；
4. 再次递归进入pos=lens-1层，经过遍历发现只有7可行，于是存入，此时得到cur[0…pos]=[1,5,2,6,4,7];
5. 再次递归进入pos=lens层，到达边界条件，所有数字都已排列好，记录下来，接下来就是不断执行类似1-5的流程，直到找到所有的全排列。

这样代码就好理解了：

class Solution:def permute(self, nums: List[int]) -> List[List[int]]:ans=[]                         #存放全部结果的数组lens=len(nums)cur=[0 for i in range(lens)]   #存放全排列的数组# permutation函数的意思是将nums里的数字进行全排列# 排列的结果存放在同样长度的cur数组中# 当前函数执行的含义是从nums数组里选择一个数字放入cur[pos]中def permutation(pos,lens,nums,cur):if(pos==lens):ans.append([i for i in cur])  #排列结束，到达边界，加入结果数组returnfor i in range(lens):             #尝试将nums[i]字放入cur[pos]中flag=0             #标记位for j in range(pos):      #如果在nums[i]已经存在于cur[0..pos-1]中，则置1if(nums[i]==cur[j]):  #因为一个数字在cur数组中只允许出现一次flag=1            #如果已经出现，那么就要继续遍历nums数组找到合适的数字if(flag==0):              #没有置1，证明nums[i]还未出现，可以选择cur[pos]=nums[i]      #将nums[i]放入cur[pos]中permutation(pos+1,lens,nums,cur) #cur[0..pos]都已经安排好，所以下一次迭代需要为cur[pos+1]找到合适的数字permutation(0,lens,nums,cur)return ans

1.2 回溯法

在上面的代码中可以发现，每次尝试放一个数字nums[i]的时候，都要判断cur[0..pos-1]中有没有出现重复，但是其实我们的目标只是看这一位数字有没有出现过（使用过）。因此可以用空间换时间的方法，使用vis数组来标记每个数字的使用情况。初始化为0，如果第i个数字被选了，则需要将vis[i]置1。因此在遍历nums数组的时候，只需要查看vis[i]==1?即可判断，只要vis[i]==0就可以选择这个数字。选择好数字之后，进行下一层的递归，当递归之后又返回到该状态时，必须将vis[i]重新设为0，以让它回到这次递归的初始状态，从而重新为这个状态选择新的数字，也能告诉下一层vis[i]可选。
Python里面如果函数的参数有列表，那么函数里对列表的修改会直接影响到列表真正的内容（有区别于cpp的虚拟传参），因此在回溯法里面，我通过使用列表形参backtracking_permutation(nums,n,lst=[])，这个函数只需要两个参数，即待全排列的数组和长度，通过lst来直接携带全排列信息，每选择一个数字，lst长度+1。与上述回溯相同的是，当前若选择了一个数字nums[i]，将其放入lst列表参数里面，然后进行下一次递归，当递归返回时，表明在当前状态下选择这个数字能走的路已经走完，所以需要使用pop删除这个数字，然后去选择其他的可能。
在这个方法中，我用flag来表示是否到达边界条件，如果在for循环中所有数字的vis都置1，那么证明所有数字都被选中，全排列结束，for循环中的flag=1无法执行，因此可以在最后通过flag==0语句把结果加入ans。否则只要还有数字没有选完，即vis数组中还有一位为0，那么在当前迭代中，flag都会被置1，因此就不会执行最后的flag==0部分代码。

class Solution:def permute(self, nums: List[int]) -> List[List[int]]:ans=[]          #所有结果数组lens=len(nums)  #需要排列的数字个数vis=[0 for i in range(lens)]  #访问数组，vis[i]标记nums[i]是否被选中，选中为1否则为0# 全排列函数，按顺序一个一个选数字# nums为需要排列的数组# lst为目前正在进行全排列的数组，存储已经选好的数字def backtracking_permutation(nums,n,lst=[]):flag=0    #标记是否已经将lens个数字全排列结束for i in range(n):   #尝试选数字if(vis[i]!=1):flag=1       #还在循环内，此vis[i]=1     #选中lst.append(nums[i])  #将选中的数字加入当前全排列backtracking_permutation(nums,n)  #选下一个数字lst.pop()     #递归函数返回后证明将nums[i]放在一个排列中的某一位的所有全排列都已找出vis[i]=0      #那么将其在这一位删除，为其找下一个可能的位置if(flag==0):  #当所有数字都被选中时，vis全部都是1，因此不会进入上面if循环ans.append([i for i in lst])  #当前lst存储的就是一个全排列，注意不能写ans.append(lst)backtracking_permutation(nums,lens)return ans

2 有重复数字全排列

leetcode实战：全排列II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

首先我们考虑用无重复紫书版本来跑一下，看看哪里出现了问题，再改进。
运行结果如下：

可以看到，结果就是没有结果。
为什么呢？因为在为cur[1]选数字的时候，首先看1，发现1已经出现，因此只能选2，然后递归到cur[2]，到cur[2]时，发现已经没有无重复数字可选，因此永远无法到达cur[3]从而储存一个全排列，这样就不会有任何全排列结果存下来。
所以，我们就需要两个参数c1、c2来记录数字使用情况。比如当考虑nums[i]时，使用c1来记录cur[0..pos-1]中nums[i]出现的情况，使用c2来记录nums数组里面出现nums[i]的次数（也可额外用字典存）。如果c1<c2，则证明nums[i]还有剩余，还能选择。
但是，如果仅仅到这里就结束，运行程序会发现，当输入为[1,1,2]时，结果会出现重复，比如多个[1,1,2],[1,2,1]…这是因为重复数字都会在同一位被选择一次，在程序看来无法识别它们之间的差异。但是其实不管是重复数字中的哪个排在这一位都是一样的结果。为了让程序知道‘不能在同一位选择相同的数字‘，需要首先对列表排序，然后在每次选位置之前加上这一句代码：**if(i==0 or nums[i]!=nums[i-1]):**就可以正确输出不重复的全排列结果了。
代码如下：

class Solution:def permuteUnique(self, nums: List[int]) -> List[List[int]]:ans=[]lens=len(nums)nums.sort()           # 排序cur=[0 for i in range(lens)]def permutation(pos,nums,n,cur):if(pos==n):ans.append([i for i in cur])returnfor i in range(n):c1=c2=0       #c1，c2分别表示目前已在全排列数组cur和nums中nums[i]出现的次数if(i==0 or nums[i]!=nums[i-1]): #如果nums[i]=nums[i-1]，那么就不必再选，否则会重复for j in range(pos):if(nums[i]==cur[j]): c1+=1for k in range(n):if(nums[i]==nums[k]): c2+=1if(c1<c2):    #证明nums[i]还能继续被选，则选中它cur[pos]=nums[i]permutation(pos+1,nums,n,cur)permutation(0,nums,lens,cur)return ans

复盘易错点（可跳过）

之前想过用回溯版本来实现重复数字全排列，在回溯版本里面加了排序和if(i==0 or nums[i]!=nums[i-1])，但是发现什么也没有输出。这是因为在选择了第一个重复数字时，进入下一层后，这个数字因为vis置1所以不会再被选，然后去找下一个数字，但是下一个重复数字因为nums[i]!=nums[i-1]被阻挡，所以永远不会被选择，其他重复数字也是一样，因此不会产生任何结果。