python实现计算精度、召回率和F1值
摘要:在深度学习的分类任务中,对模型的评估或测试时需要计算其在验证集或测试集上的预测精度(prediction/accuracy)、召回率(recall)和F1值。本文首先简要介绍如何计算精度、召回率和F1值,其次给出python编写的模块,可直接将该模块导入在自己的项目中,最后给出这个模块的实际使用效果。
一、混淆矩阵及P、R、F1计算原理
1、混淆矩阵
在进行二分类或多分类任务中,对于预测的评估经常需要构建一个混淆矩阵来表示测试集预测类与实际类的对应关系,混淆矩阵横坐标表示实际的类,纵坐标表示预测的类。混淆矩阵属于 n × n n\times n n×n 方阵,其中 n n n 表示类的个数。矩阵可用下面表示:
c o n f m a r t i x ( t r u e L a b e l , p r e d i c t L a b e l ) confmartix(trueLabel,predictLabel) confmartix(trueLabel,predictLabel)
因此该矩阵的某一个元素 c o n f m a r t i x ( i , j ) confmartix(i,j) confmartix(i,j) 表示实际类 i i i 被预测成 j j j 的样本个数。很显然,当前仅当 i = j i=j i=j ,即矩阵的主对角线上的元素表示被预测正确的。
2、P、R、F1值
基于混淆矩阵可以很轻松的计算出精度、召回率和F1值,以及微平均和宏平均。
-
样本的总体精度(微平均,all_prediction):混淆矩阵主对角线上元素和除以混淆矩阵所有元素和。公式为:
a l l _ p r e d i c t i o n = s u m ( d i a g ( c o n f m a r t i x ) ) s u m ( c o n f m a r t i x ) all\_prediction=\frac{sum(diag(confmartix))}{sum(confmartix)} all_prediction=sum(confmartix)sum(diag(confmartix)) -
某个类 i i i 的精度(label_i_prediction):元素 c o n f m a r t i x ( i , i ) confmartix(i,i) confmartix(i,i) 除以下标为 i i i 的纵坐标元素和。公式为:
l a b e l _ i _ p r e d i c t i o n = c o n f m a r t i x ( i , i ) ∑ j c o n f m a r t i x ( j , i ) label\_i\_prediction=\frac{confmartix(i,i)}{\sum_j{confmartix(j,i)}} label_i_prediction=∑jconfmartix(j,i)confmartix(i,i) -
某各类 i i i 的召回率(label_i_recall):元素 c o n f m a r t i x ( i , i ) confmartix(i,i) confmartix(i,i) 除以下标为 i i i 的横坐标元素和。公式为:
l a b e l _ i _ r e c a l l = c o n f m a r t i x ( i , i ) ∑ j c o n f m a r t i x ( i , j ) label\_i\_recall=\frac{confmartix(i,i)}{\sum_j{confmartix(i,j)}} label_i_recall=∑jconfmartix(i,j)confmartix(i,i) -
样本的总体召回率(宏平均 MACRO-averaged): 所有类的召回率的平均值。公式为:
a l l _ r e c a l l = a v g ( ∑ i l a b e l _ i _ r e c a l l ) all\_recall=avg(\sum_i{label\_i\_recall}) all_recall=avg(i∑label_i_recall) -
样本的总体精度(宏平均 MACRO-averaged):区别于第一个,宏平均为所有类的精度的均值。公式为:
a l l _ p r e d i c t i o n = a v g ( ∑ i l a b e l _ i _ p r e d i c t i o n ) all\_prediction=avg(\sum_i{label\_i\_prediction}) all_prediction=avg(i∑label_i_prediction) -
F1值:总体样本(或某个类)的精度和召回率满足如下:
F 1 = 2 × p r e d i c t i o n × r e c a l l p r e d i c t i o n + r e c a l l F1=\frac{2\times prediction \times recall}{prediction + recall} F1=prediction+recall2×prediction×recall
3、样例计算
为了更加清楚的理解上面的计算公式,给出一个关系抽取的实例,例如下面的混淆矩阵,横坐标为实际类,纵坐标为预测的类,一共19个类。

总体均值为: 2052 / 2717 = 75.52 % 2052/2717=75.52\% 2052/2717=75.52%
各个类的精度、召回率和F1值为: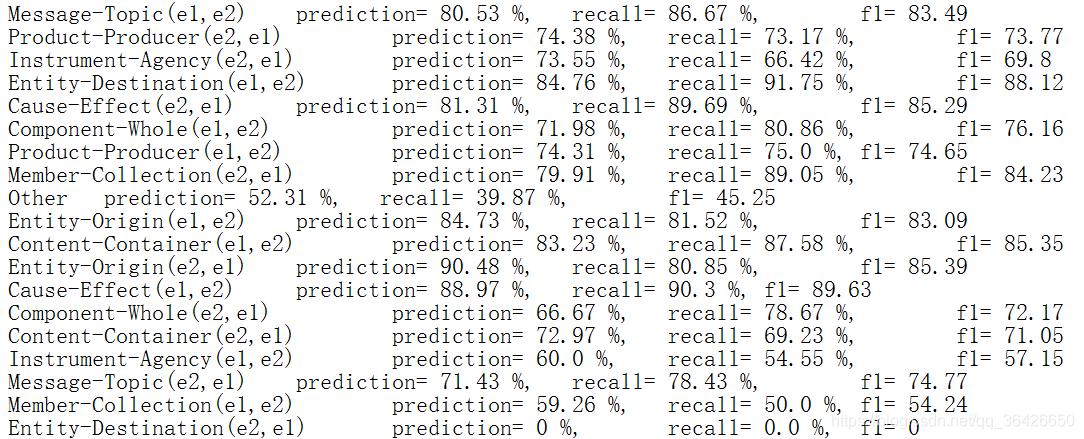
宏平均精度为 71.09 % 71.09\% 71.09%、宏平均召回率为 71.77 % 71.77\% 71.77%、F1值为 71.43 71.43 71.43。
二、python模块
为了在实际实验中更快捷的计算相应值,许多集成的perl脚本可以很轻松的实现计算,但为了更加方便用户编辑以及无缝接入自己的项目中,本文实现python的简单脚本。用户仅需import即可调用,源码如下:
#####模块说明######
'''
根据传入的文件true_label和predict_label来求模型预测的精度、召回率和F1值,另外给出微观和宏观取值。
powered by wangjianing 2019.3.2'''
import numpy as npdef getLabelData(file_dir):'''模型的预测生成相应的label文件,以及真实类标文件,根据文件读取并加载所有label1、参数说明:file_dir:加载的文件地址。文件内数据格式:每行包含两列,第一列为编号1,2,...,第二列为预测或实际的类标签名称。两列以空格为分隔符。需要生成两个文件,一个是预测,一个是实际类标,必须保证一一对应,个数一致2、返回值:返回文件中每一行的label列表,例如['true','false','false',...,'true']'''labels = []with open(file_dir,'r',encoding="utf-8") as f:for i in f.readlines():labels.append(i.strip().split(' ')[1])return labelsdef getLabel2idx(labels):'''获取所有类标返回值:label2idx字典,key表示类名称,value表示编号0,1,2...'''label2idx = dict()for i in labels:if i not in label2idx:label2idx[i] = len(label2idx)return label2idxdef buildConfusionMatrix(predict_file,true_file):'''针对实际类标和预测类标,生成对应的矩阵。矩阵横坐标表示实际的类标,纵坐标表示预测的类标矩阵的元素(m1,m2)表示类标m1被预测为m2的个数。所有元素的数字的和即为测试集样本数,对角线元素和为被预测正确的个数,其余则为预测错误。返回值:返回这个矩阵numpy'''true_labels = getLabelData(true_file)predict_labels = getLabelData(predict_file)label2idx = getLabel2idx(true_labels)confMatrix = np.zeros([len(label2idx),len(label2idx)],dtype=np.int32)for i in range(len(true_labels)):true_labels_idx = label2idx[true_labels[i]]predict_labels_idx = label2idx[predict_labels[i]]confMatrix[true_labels_idx][predict_labels_idx] += 1return confMatrix,label2idxdef calculate_all_prediction(confMatrix):'''计算总精度:对角线上所有值除以总数'''total_sum = confMatrix.sum()correct_sum = (np.diag(confMatrix)).sum()prediction = round(100*float(correct_sum)/float(total_sum),2)return predictiondef calculate_label_prediction(confMatrix,labelidx):'''计算某一个类标预测精度:该类被预测正确的数除以该类的总数'''label_total_sum = confMatrix.sum(axis=0)[labelidx]label_correct_sum = confMatrix[labelidx][labelidx]prediction = 0if label_total_sum != 0:prediction = round(100*float(label_correct_sum)/float(label_total_sum),2)return predictiondef calculate_label_recall(confMatrix,labelidx):'''计算某一个类标的召回率:'''label_total_sum = confMatrix.sum(axis=1)[labelidx]label_correct_sum = confMatrix[labelidx][labelidx]recall = 0if label_total_sum != 0:recall = round(100*float(label_correct_sum)/float(label_total_sum),2)return recalldef calculate_f1(prediction,recall):if (prediction+recall)==0:return 0return round(2*prediction*recall/(prediction+recall),2)def main(predict_file,true_file):'''该为主函数,可将该函数导入自己项目模块中打印精度、召回率、F1值的格式可自行设计'''#读取文件并转化为混淆矩阵,并返回label2idxconfMatrix,label2idx = buildConfusionMatrix(predict_file,true_file)total_sum = confMatrix.sum()all_prediction = calculate_all_prediction(confMatrix)label_prediction = []label_recall = []print('total_sum=',total_sum,',label_num=',len(label2idx),'\n')for i in label2idx:print(' ',i)print(' ')for i in label2idx:print(i,end=' ')label_prediction.append(calculate_label_prediction(confMatrix,label2idx[i]))label_recall.append(calculate_label_recall(confMatrix,label2idx[i]))for j in label2idx:labelidx_i = label2idx[i]label2idx_j = label2idx[j]print(' ',confMatrix[labelidx_i][label2idx_j],end=' ')print('\n')print('prediction(accuracy)=',all_prediction,'%')print('individual result\n')for ei,i in enumerate(label2idx):print(ei,'\t',i,'\t','prediction=',label_prediction[ei],'%,\trecall=',label_recall[ei],'%,\tf1=',calculate_f1(label_prediction[ei],label_recall[ei]))p = round(np.array(label_prediction).sum()/len(label_prediction),2)r = round(np.array(label_recall).sum()/len(label_prediction),2)print('MACRO-averaged:\nprediction=',p,'%,recall=',r,'%,f1=',calculate_f1(p,r))
使用说明:
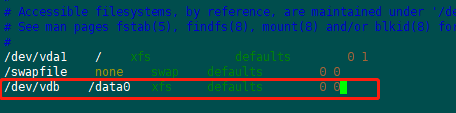
1、在自己的项目中,做模型的测试时,需要将实际类及预测类分别写入文件,格式例如下图:第一列为编号,第二列为类,中间用一个字符的空格隔开。
2、在测试的文件中添加导入模块语句
import prf1(假设这个脚本保存为 prf1.py)
3、模型预测后,执行(其中predict_file和true_file分别表示预测类文件和实际类文件):
prf1.main(predict_file,true_file)
备注:当然大家可以自己设计main函数中的打印格式
三、使用效果
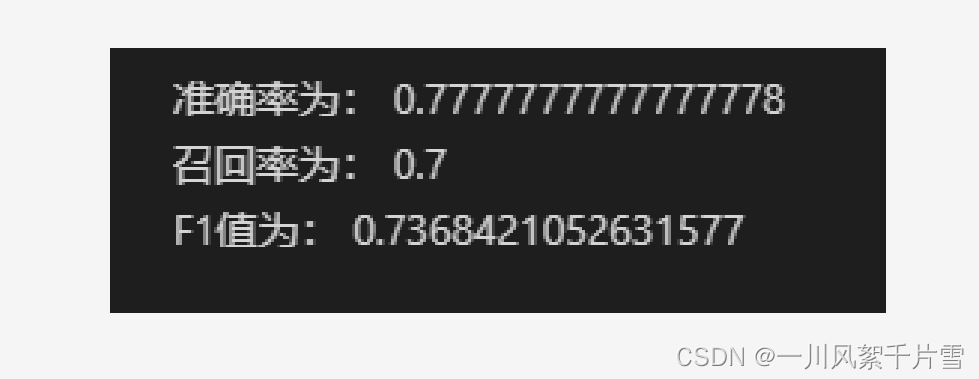
博主将该脚本用在自己的实验中,做关于中文学科知识点关系抽取实验中,输出效果如图:
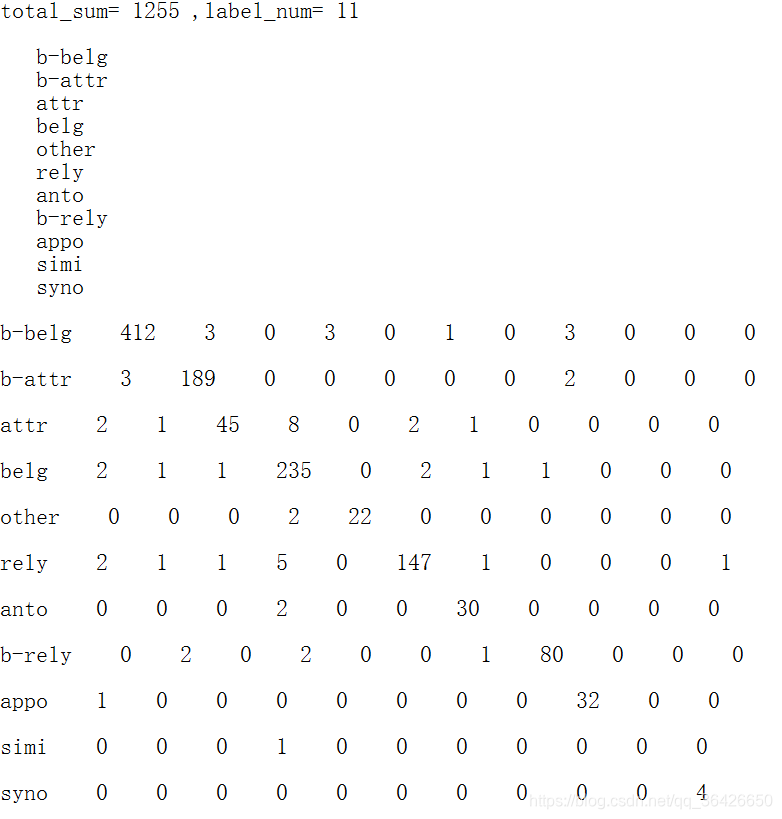

博客记录着学习的脚步,分享着最新的技术,非常感谢您的阅读,本博客将不断进行更新,希望能够给您在技术上带来帮助。欢迎转载,转载请注明出处