GPR(高斯过程回归)详细推导

一、综述

GPR来源于线性模型，有两种方式可以推导出GPR，一种是weight space view,另外一种是function space view。两者考察方式假设不同，关注的对象不同，但是最后导出的结果是相同的。其中，function view的推导方式更加简单，GPR最终的为了实现回归，即已知X,y,x*,求y*。最终的推导出的公式如下：

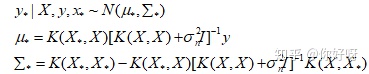
X,y是已知的数据，我们要求未知数据x*处的函数值，K是核函数。我们接下来会从weight space view和function space view两种方式推导出GPR。最后一部分是GPR的算法流程图。

参考资料：

1.《Gaussian Processes for Machine Learning》

2. https://www.bilibili.com/video/BV1aE411o7qd?p=114

3. https://zhuanlan.zhihu.com/p/75589452 (python的代码演示，包含可视化)

4. python的GPy库和MATLAB中的ooDACE里面集成有GPR

二、weight space view(将w看作变量)

我们考虑下面一个问题：

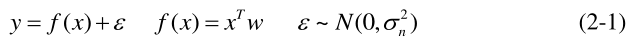
这是一个线性模型，GPR的想法就是把w看做正态分布的随机变量，求出了w的分布，就知道了y的分布。这里的ε是噪声，在推导中是必须的。如果把

ε=0就是一个无噪的预测，考虑到ε的影响就是一个有噪声的预测。

整个推导分成三部分：

1.已知w的先验分布，通过更多的数据(X,y)求得w的后验分布

2.已知w的后验分布，就能求得f*的概率分布(可以简单地理解为用

来代替)

3.将f*概率分布中均值和方差写成核函数的形式，这个形式与function space view推导出的结果一致，完成！

注：本文的所有推导前面是推导的主干部分，细致的证明在后面。

2.1 w的后验分布

如果我们已经知道了w的确定值，要预测xi处的函数值yi可以表达如下：

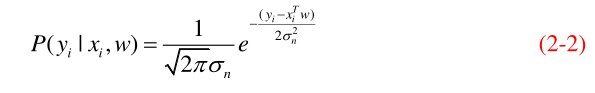
上述公式写出了某一点的预测值yi,如果有多个点的值需要预测，将每个点的值看作是独立的，可以得到

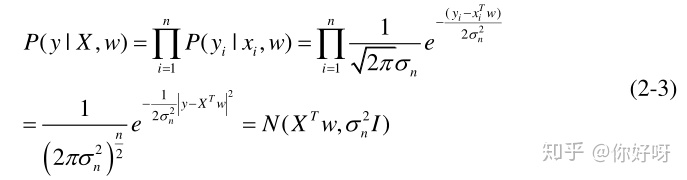
由于我们不知道w的分布是怎样的，我们可以假设w的先验为,p是代表先验prior的意思。

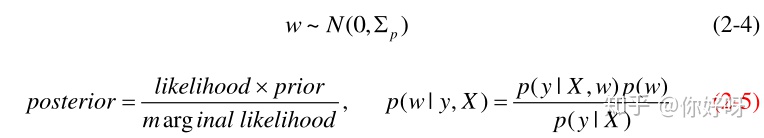
这里的p(y|X)是marginal likelihood, GPR中的超参数调节就是使得marginal likelihood最大！