文章目录
- 0. 评价指标
- 1. 工具箱拟合——cftool
- 2. 万能拟合 ——nlinfit
- 3. 多项式拟合 ——polyfit
- 参考
0. 评价指标
一、SSE(和方差)
该统计参数计算的是拟合数据和原始数据对应点的误差的平方和,计算公式如下
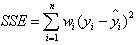
SSE越接近于0,说明模型选择和拟合更好,数据预测也越成功。接下来的MSE和RMSE因为和SSE是同出一宗,所以效果一样
二、MSE(均方差)
该统计参数是预测数据和原始数据对应点误差的平方和的均值,也就是SSE/n,和SSE没有太大的区别,计算公式如下
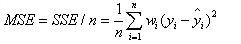
三、RMSE(均方根)
该统计参数,也叫回归系统的拟合标准差,是MSE的平方根,就算公式如下
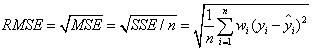
在这之前,我们所有的误差参数都是基于预测值(y_hat)和原始值(y)之间的误差(即点对点)。从下面开始是所有的误差都是相对原始数据平均值(y_ba)而展开的(即点对全)!!!
四、R-square(确定系数)
在讲确定系数之前,我们需要介绍另外两个参数SSR和SST,因为确定系数就是由它们两个决定的
(1)SSR:Sum
of squares of the regression,即预测数据与原始数据均值之差的平方和,公式如下
(2)SST:Total sum of squares,即原始数据和均值之差的平方和,公式如下
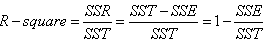
细心的网友会发现,SST=SSE+SSR,呵呵只是一个有趣的问题。而我们的“确定系数”是定义为SSR和SST的比值,故
其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0
1],越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好。
1. 工具箱拟合——cftool

在命令行输入数据:
x
y
启动曲线拟合工具箱
命令:cftool
进入曲线拟合工具箱界面“Curve Fitting tool”
1)利用X data和Y data的下拉菜单读入数据x,y
2)选择曲线拟合类型
3)自动拟合 即可在结果窗口和曲线窗口显示出拟合结果
工具箱提供的拟合类型如下,进行简要说明,可以尝试各种不同类型拟合效果
| 英文名称 | 逼近类型 | 种类数量 | 基础类型 |
|---|---|---|---|
| Custom Equations | 用户自定义的函数类型 | ||
| Exponential | 指数逼近 | 2 | |
| Fourier | 傅立叶逼近 | 7 | |
| Gaussian | 高斯逼近 | 8 | |
| Interpolant | 插值逼近 | 4 | linear、nearest neighbor、cubic spline、shape-preserving |
| Polynomial | 多形式逼近 | 9 | linear ~、quadratic ~、cubic ~、4-9th degree ~ |
| Power | 幂逼近 | 2 | ax^b 、ax^b + c |
| Rational | 有理数逼近 | ,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型 | |
| Smoothing Spline | 平滑逼近 | ||
| Sum of Sin Functions | 正弦曲线逼近 | 8 | a1sin(b1x + c1) |
| Weibull | 1 | abx(b-1)*exp(-a*xb) |
注意 : Interpolant是插值逼近仅仅是对函数进行插值画图显示,并不能得到拟合的函数。
Exponential:指数逼近,有2种类型, aexp(bx) 、 aexp(bx) + cexp(dx)
Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1cos(xw) + b1sin(xw)
Gaussian:高斯逼近,有8种类型,基础型是 a1exp(-((x-b1)/c1)^2)
Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving
Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~
Power:幂逼近,有2种类型,ax^b 、ax^b + c
Rational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型
Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思)
Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1sin(b1x + c1)
Weibull:只有一种,ab*x(b-1)*exp(-a*xb)
选择View > Residuals Plot,可以查看残差图。
在Table of Fits中右击选择Duplicate “XX” (或者在Fit主菜单里面复制) 复制某个拟合,重新生成别的拟合,进行对比。
观察Results以及residuals plot 残差图。
The residuals from a good fit should look random with no apparent pattern. A pattern, such as a tendency for consecutive residuals to have the same sign, can be an indication that a better model exists.
2. 万能拟合 ——nlinfit
matlab 万能实用的非线性曲线拟合方法 - It’s All Uphill From Here
matlab函数拟合 - 学习时间轴 - 博客园
clear
clc %清除工作空间
syms x;%公共参数设置
xx=[3,5]'; %这里设置已知自变量向量(列向量)
yy = [0.8,1]'; %对应因变量(列向量)
startPos = [1,1]; %设置系数的起始搜索点
%使用fit函数拟合的
%设置参数
f = '(1+alpha*(x-belta)^(-2))^(-1)'; %设置需要拟合的函数形式
funType=fittype(f,'independent','x',...
'coefficients',{'alpha','belta'}); %在independent后面设置自变量,在coefficients后面设置待定系数(多个值用{}括起来)
%使用nlinfit函数进行拟合的
%设置参数
f1 = @(coef,x)(1+coef(1)*(x-coef(2)).^(-2)).^(-1); %设置需要拟合的函数(内联函数形式)%后面的代码不用改
%fit拟合相关代码
opt=fitoptions(funType);
set(opt,'StartPoint',startPos);
cfun=fit(xx,yy,funType,opt) %命令行显示结果
plot(cfun,'r',xx,yy,'*')%nlinfit拟合相关代码
coef=nlinfit(xx,yy,f1,startPos);
disp('nlinfit拟合后的系数矩阵为:');
disp(coef);hold on
xmax = max(xx);
xmin = min(xx);
xnum = 2*length(xx)+50;
x = linspace(xmin,xmax,xnum);
y = f1(coef,x);
plot(x,y,'g');legend('原始数据','fit拟合','nlinfit拟合')
3. 多项式拟合 ——polyfit
p=polyfit(x,y,2);
如何使用MATLAB进行曲线拟合-百度经验
| Library Model Name | Description |
|---|---|
| poly1 | 线性多项式曲线 |
| poly11 | 线性多项式表面 |
| poly2 | 二次多项式曲线 |
| linearinterp | 分段线性插值 |
| cubicinterp | 分段三次插值 |
| smoothingspline | 平滑样条(曲线) |
| lowess | 局部线性回归(曲面) |
参考
matlab 万能实用的非线性曲线拟合方法 - It’s All Uphill From Here