1. 关于灰色关联分析

1.1. 什么是灰色关联分析

灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法，其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密，它反映了曲线间的关联程度。

在系统发展过程中，若两个因素变化的趋势具有一致性，即同步变化程度较高，即可谓二者关联程度较高；反之，则较低。因此，灰色关联分析方法，是根据因素之间发展趋势的相似或相异程度，亦即“灰色关联度”，作为衡量因素间关联程度的一种方法。

灰色系统理论提出了对各子系统进行灰色关联度分析的概念，意图透过一定的方法，去寻求系统中各子系统（或因素）之间的数值关系。因此，灰色关联度分析对于一个系统发展变化态势提供了量化的度量，非常适合动态历程分析。

也就是说，灰色关联分析的研究对象往往是一个系统。系统的发展会受到多个因素的影响。我们常常想知道，在众多的影响因素中，哪些是主要因素，哪些是次要因素；哪些因素影响大，哪些因素影响小；哪些具有促进作用，哪些具有抑制作用等等。

关联度，是表征两个事物之间的关联程度，在数学上是指两函数相似的程度。

1.2. 灰色关联分析的使用

通常可以运用此方法来分析各个因素对于结果的影响程度，也可以运用此方法解决随时间变化的综合评价类问题，其核心是按照一定规则确立随时间变化的母序列（参考列），把各个评估对象随时间的变化作为子序列，求各个子序列与母序列（参考列）的相关程度，依照相关性大小得出结论。

灰色系统理论是由著名学者邓聚龙教授首创的一种系统科学理论(Grey Theory)，其中的灰色关联分析是根据各因素变化曲线几何形状的相似程度，来判断因素之间关联程度的方法。

此方法通过对动态过程发展态势的量化分析，完成对系统内时间序列有关统计数据几何关系的比较，求出参考数列与各比较数列之间的灰色关联度，与参考数列关联度越大的比较数列，其发展方向和速率与美考数列越接近，与参考数列的关系越紧密。

灰色关联分析方法要求样本容量可以少到4个，对数据无规律同样适用，不会出现量化结果与定性分析结果不符的情况，其基本思想是将评价指标原始观测数进行无量细化处理、计算关联系数、关联度以及根据关联度的大小对待评指标进行排序。

灰色关联度的应用涉及社会科学和自然科学的各个领域，尤其在社会经济领域，如国民经济各部门投资收益、区域经济优势分析、产业结构调整等方面，都取得较好的应用效果。

关联度有绝对关联度和相对关联度之分，绝对关联度采用初始点零化法进行初值化处理，当分析的因素差异较大时，由于变量间的量纲不一致，往往影响分析，难以得出合理的结果。而相对关联度用相对量进行分析，计算结果仅与序列相对于初始点的变化速率有关，与各观测数据大小无关，这在一定程度上弥补了绝对关联度的缺陷。

1.3. 灰色关联分析的基本特征

(1). 总体性

灰色关联度虽是数据序列几何形状的接近程度的度量，但它一般强调的是若干个数据序列对一个既定的数据序列接近的相对程度，即要排出关联度大小的顺序，这就是总体性，其将各因素统一置于系统之中进行比较与分析。

(2). 非对称性

在同一系统中，甲对乙的关联度，并不等于乙对甲的关联度，这较真实地反映了系统中因素之间真实的灰关系。

(3). 非唯一性
关联度随着参考序列不同、因素序列不同、原始数据处理方法不同、数据多少不同而不同。

(4). 动态性
因素间的灰色关联度随着序列的长度不同而变化，表明系统在发展过程中，各因素之间的关联关系也随着时间不断变化。

1.4. 灰色关联分析与大数据及其他数理统计比较

数理统计中常常使用回归分析、方差分析、主成分分析等来探究这个问题。但上述的方法有一些共同的不足之处。例如这些方法都要求大量的数据，数据小则结果没有太大意义；有时候还会要求样本服从某个特殊分布，或者出现量化结果与定性分析不符合的情况。而灰色关联分析则可以较好地应对这些问题。

灰色关联分析对样本量的多少和样本有无规律并没有要求（当然样本量也不能太少，就两、三个样本还分析什么），量化结果基本上与定性分析相符合。灰色关联分析的基本思想是，根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的关联度就越大，反之就越小。

对于上述原理，简单翻译一下，就是研究两个或多个序列（序列可以理解为系统中因素或者指标）构成的曲线的几何相似程度。越相似，越说明他们的变化具有某种紧密的联系，也就是关联度高。所以这个方法也几乎是从纯数据的角度去研究关联性，如果两个没啥关系的指标，在曲线形状上表现得极为相似，那灰色关联分析就会认为二者关联程度很高。当然这只是一个比较极端的例子，对于一般的数据或者系统，用曲线形状来衡量关联度，也是有一定的道理的。

2. 灰色关联分析的过程

2.1．根据分析目的确定分析指标体系，收集分析数据。

下表为某地区国内生产总值的统计数据（以百万元计），问该地区从2000年到2005年之间哪一种产业对GDP总量影响最大。

年份	国内生产总值	第一产业	第二产业	第三产业
2000	1988	386	839	763
2001	2061	408	846	808
2002	2335	422	960	953
2003	2750	482	1258	1010
2004	3356	511	1577	1268
2005	3806	561	1893	1352

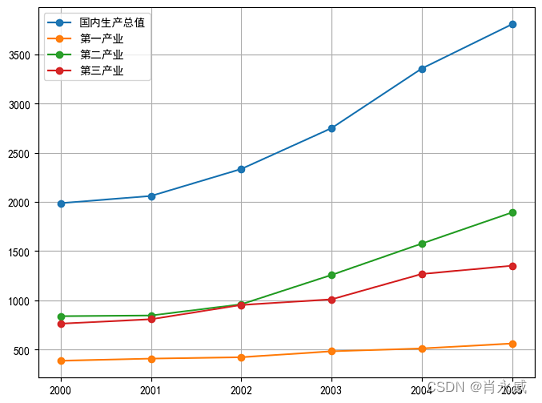
在这里插入图片描述

谁与国内生产总值关联度最高
哪个产业发展的更好
哪年发展的较优秀

设 $n$ 个数据序列形成如下矩阵：

$(X'_1,X'_2,...,X'_n)=\begin{pmatrix} x'_1(1) & x'_2(1) & ... & x'_n(1)\\ x'_1(2) & x'_2(2) & ... & x'_n(2)\\ ... & ... & ... & ...\\ x'_1(m) & x'_2(m) & ... & x'_n(m) \end{pmatrix}$

其中 $m$ 为指标的个数， $X'_i=(x'_i(1),x'_i(2),...,x'_i(m))^T, i=1,2,...,n$ 。

2.2．确定参考数据列

通常，根据分析目标确定参考数据列：

目标一，指标排序选优，指标体系中的指标与对标指标的关联度的大小，并可以数值大小排序。

按业务选择理想比较基准，例如在此需要分别将三种产业与国内生产总值比较计算其关联程度，故参考序列为国内生产总值。

目标二，综合评价，评价指标，给出量化数值，以及的优良顺序。

若是解决综合评价问题时则参考序列可能需要自己生成，通常选定每个指标或时间段中所有子序列中的最佳值组成的新序列为参考序列。
参考数据列应该是一个理想的比较标准，可以以各指标的最优值（或最劣值）构成参考数据列，也可根据评价目的选择其它参照值．

谁与国内生产总值关联度最高？选择国内生产总值列为参考列。
哪个产业发展的更好，选择每个指标的最优值（最大）值，手工生成参考数列。
哪年发展的较优秀，选择各个年度的最优值，手工生产参考数列。

参考数列记作：
$X'_0=(x'_0(1),x'_0(2),...,x'_0(m))$

2.3．对指标数据进行无量纲化

由于系统中各因素的物理意义不同，导致数据的量纲也不一定相同，不便于比较，或在比较时难以得到正确的结论。因此在进行灰色关联度分析时，一般都要进行无量纲化的数据处理。

常用无量纲方法之一：

$x_{i}(k)=\frac{x'_{i}(k)}{\frac{1}{m}\sum_{k=1}^{m}x'_{i}(k) }$

无量纲化后的数据序列形成如下矩阵：

$(X_1,X_2,...,X_n)=\begin{pmatrix} x_1(1) & x_2(1) & ... & x_n(1)\\ x_1(2) & x_2(2) & ... & x_n(2)\\ ... & ... & ... & ...\\ x_1(m) & x_2(m) & ... & x_n(m) \end{pmatrix}$

2.4．求解参考序列和特征序列之间的灰色关联系数值

（1）求差序列

逐个计算每个被评价对象指标序列（比较序列）与参考序列对应元素的绝对差值
$\Delta x_i(k)=|x_i(k)-x_0(k)|, k=1,2,...m ; i=1,2,...,n$

其中 , $n$ 为被评价对象的个数。

（2）求两极差
$\underset{i}{min} \underset{k}{min} |x_{0}(k)-x_{i}(k)|$

$\underset{i}{max} \underset{k}{max} |x_{0}(k)-x_{i}(k)|$

（3）求关联系数
$\zeta _{i}(k)=\frac{\underset{i}{min} \underset{k}{min} |x_{0}(k)-x_{i}(k)|+\rho\cdot \underset{i}{max} \underset{k}{max} |x_{0}(k)-x_{i}(k)|}{|x_{0}(k)-x_{i}(k)|+\rho\cdot \underset{i}{max} \underset{k}{max} |x_{0}(k)-x_{i}(k)|}$

其中， $k = 1, ..., m$ 。 $\rho$ 为分辨系数，取值在 $(0, 1)$ ，若 $\rho$ 越小，关联系数间差异越大，区分能力越强，通常 $\rho$ 取0.5。

2.5．计算关联度

对各评价对象（比较指标序列）分别计算各个指标与参考序列对应元素的关联系数的均值，以反映各评价对象与参考序列的关联关系，并称其为关联序，记为：

$r_i = \frac{1}{m}\sum_{k=1}^{m} \zeta _{i}(k)$

2.6．综合评价

如果各指标在综合评价中所起的作用不同，可对关联系数求加权平均值即：

$r_i = \frac{1}{m}\sum_{k=1}^{m} W_i\zeta _{i}(k)$

其中， $W_i$ 为各个指标的权重。

3. Python实践过程

3.1. 定义关联度计算函数

# dd为输入数据表，m为参数列，默认为0，如果flag为非None，则可任意值，无意义
# flag 标识参考列方式，默认None是按列取值
# flag = 'MAX' 按最大值取值
# flag = 'MIN' 按最小值取值def GRA(dd, m=0, flag=None):# 读取为df格式#dd = dimensionlessProcessing(dd)x_mean=dd.mean(axis=0)#print(x_mean)for i in range(len(dd.columns)):dd.iloc[:,i] = dd.iloc[:,i]/x_mean[i]    # 参考要素if flag==None:std = dd.iloc[:, m]  # 为参考要素dd.drop(dd.columns[m],axis=1,inplace=True)        elif flag=='MAX':std = dd.max(axis=1)elif flag=='MIN':std = dd.min(axis=1)else:print('flag eorro!')return Noneprint(std)print(dd)shape_n, shape_m = dd.shape[0], dd.shape[1]  # 计算行列# 与参考要素比较，相减a = zeros([shape_m, shape_n])for i in range(shape_m):for j in range(shape_n):a[i, j] = abs(dd.iloc[j, i] - std[j])# 取出矩阵中最大值与最小值print(a)c, d = a.max().max(), a.min().min()print(c,d)# 计算关联系数result = (d + 0.5 * c) / (a + 0.5 * c)# 求均值，得到灰色关联度,并返回result_list = [mean(result[i, :]) for i in range(shape_m)]return pd.DataFrame(result_list)

3.2. 指标排序

计算关联度及图例：

import pandas as pd
import numpy as np
from numpy import *
import matplotlib.pyplot as plt
%matplotlib inlinex = pd.DataFrame([[1988,2061,2335,2750,3356,3806],[386,408,422,482,511,561], [839,846,960,1258,1577,1893], [763,808,953,1010,1268,1352]])
x.columns = ['2000','2001','2002','2003','2004','2005']
x.index = ['国内生产总值','第一产业','第二产业','第三产业']
dd = x.Tplt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False  
dd.plot(kind='line',figsize=(8,6),grid=True,marker='o')
dd

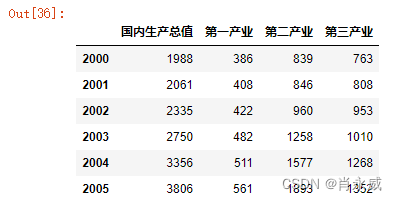
在这里插入图片描述

df = x.iloc[:,:].T.copy()print(df)
data_gra = GRA(df, m=0)
data_gra

参考列：
在这里插入图片描述
无量纲矩阵：

求解差序列矩阵：
在这里插入图片描述

求解两级差：0.186163, 0.000628。

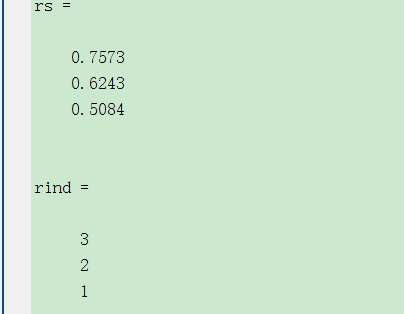
关联度序：
第一产业： 0.508432，第二产业：0.624296，第三产业：0.757300

3.3. 综合评价

df = x.iloc[:,:].T.copy()print(df)
data_gra = GRA(df, flag='MAX')
data_gra

求解两级差：0.325323， 0.0

综合评价：

国内生产总值：0.671001
第一产业：0.788028
第二产业：0.730317
第三产业：0.699678

4. 总结

指标排序，可以得到 $r_01 = 0.5088，r_02= 0.6248， r_03= 0.7577$ ，通过比较三个子指标序列与参考序列的关联度可以得出结论：该地区在2000年到2005年期间的国内生产总值受到第三产业的影响最大。

综合评价，可以得到 $r 0 = 0.671001 ， r 1 = 0.788028 ， r 2 = 0.730317 ， r 3 = 0.699678$ ，通过比较指标综合评价可以得出结论：该地区在2000年到2005年期间，第一产业的发展最好。

灰色关联分析主要有两个作用，一是进行系统发展影响因素分析，诊断影响系统发展的重要因素。第二个作用就是用于综合评价问题，给出研究对象或者方案的优劣排名，可用于经营管理咨询工作。

灰色关联分析方法的优点在于思路明晰，可以在很大程度上减少由于信息不对称带来的损失，并且对数据要求较低，工作量较少；其主要缺点在于要求需要对各项指标的最优值进行现行确定，主观性过强，同时部分指标最优值难以确定。

5. 后续应用思考

综合评价2000年到2005年间发展情况，相当于2000年到2005年成为6项指标。

df = x.iloc[:,:].copy()print(df)
data_gra = GRA(df, flag='MAX')
data_gra

综合评价计算结果是：
2000， 0.731977
2001， 0.764135
2002， 0.763014
2003， 0.673676
2004， 0.672552
2005， 0.728462
结论是2001年综合评价最优，再分析此时的第一产业、第二产业、第三产业构成。

如此，把灰色关联分析方法应用到企业经营分析上，由于企业经营数据偏少，大数据方法不太适应，因此，我们把企业好比一个灰色系统，挖掘有限数据的价值，对可识别的指标进行分析。

由于作者水平有限，欢迎留言讨论！

参考：

[1]. Font Tian. Python实现灰色关联分析与结果可视化. CSDN博客. 2018.06
[2]. 我不爱机器学习. python实现灰色关联法(GRA). CSDN博客. 2022.11
[3]. spssau. [学习资料] 灰色关联法如何分析？. 经管之家. 2022.09
[4]. 李响Superb. 机器学习（MACHINE LEARNING）灰色关联分析(GRA). 51CTO博客. 2021.06
[5]. 木子. 灰色关联算法原理与实现详解. 知乎. 2022.04
[6]. 回到唐朝当少爷. 清风数学建模Python代码——灰色关联分析. 哔哩哔哩. 2022.10
[7]. 灰色关联分析. MBA智库百科
[8]. 小白. 数学建模笔记——评价类模型之灰色关联分析. 知乎. 2020.07
[9]. 杨辰, 高寒歌. 灰色预测模型与灰色关联度分析在公司运营中的应用. 财经与管理. 2019.03. 12-18
[10]. 王本刚. 灰色关联和层次分析法在加油站安全评价中的应用. 中国石油和化工标准与质量. 2017,（16）
[11]. 方少林，孟路园，霍俊. 基于熵权法与灰色关联分析法的加油站油罐区安全评价. 山东化工. 2020,（17）