正则化是一种为了减小测试误差的行为(有时候会增加训练误差)。当我们用较为复杂的模型拟合数据时，容易出现过拟合现象，导致模型的泛化能力下降，这时我们就需要使用正则化，降低模型的复杂度。本文总结阐释了正则化的相关知识点，帮助大家更好的理解正则化这一概念。

目录

• LP范数

• L1范数

• L2范数

• L1范数和L2范数的区别

• Dropout

• Batch Normalization

• 归一化、标准化 & 正则化

• Reference

在总结正则化（Regularization）之前，我们先谈一谈正则化是什么，为什么要正则化。

个人认为正则化这个字眼有点太过抽象和宽泛，其实正则化的本质很简单，就是对某一问题加以先验的限制或约束以达到某种特定目的的一种手段或操作。在算法中使用正则化的目的是防止模型出现过拟合。一提到正则化，很多同学可能马上会想到常用的L1范数和L2范数，在汇总之前，我们先看下LP范数是什么鬼。

LP范数

范数简单可以理解为用来表征向量空间中的距离，而距离的定义很抽象，只要满足非负、自反、三角不等式就可以称之为距离。

LP范数不是一个范数，而是一组范数，其定义如下：

 

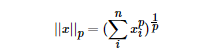
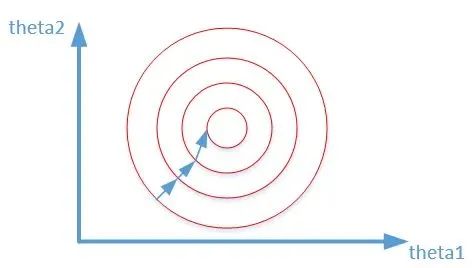
pp的范围是[1,∞)[1,∞)。pp在(0,1)(0,1)范围内定义的并不是范数，