典型应用——文本分类
1)文本信息的表示,从原始的文本转化为结构化的可处理信息;
2)目前常采用向量空间模型来描述文本向量,通常文本向量维度较高,使得分类效率低下;
3)必须对特征向量进行降维处理,最有效的方法是特征选择。
文本特征向量提取
1)空间向量模型:将文本内容转化为向量空间中的向量运算,以空间上的相似度表示语义上的相似度。
2)文本处理中常用的相似性度量方式是余弦距离。
3)设D为一个包含m个文档的文档集合,Di为第i个文档的特征向量,则有:
D={D1,D2,…,Dm}, 其中 Di=(di1,di2,…,din),i=1,2,…,m,dij(i=1,2,…,m;j=1,2,…,n)为
文档Di中第j个词条tj的权值,它一般被定义为tj在Di中出现的频率tij的函数,例如采用TF-IDF函数,
即dij=tij*log(N/nj)其中,N是文档数据库中文档总数,nj是文档数据库含有词条tj的文档数目。
4)通过上述的空间向量模型,文本数据转化成了计算机可处理的结构化数据,文本之间的相似性问题也转化成了向量之间的相似性问题。
文本特征向量选择
1. TF-IDF的局限性
TF-IDF可以有效评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。因为它综合表征了该词在文档中的重要程度和文档区分度。但在文本分类中单纯使用TF-IDF来判断一个特征是否有区分度是不够的。
1)它没有考虑特征词在类间的分布。也就是说该选择的特征应该在某类出现多,而其它类出现少,即考察各类的文档频率的差异。如果一个特征词,在各个类间分布比较均匀,这样的词对分类基本没有贡献;但是如果一个特征词比较集中的分布在某个类中,而在其它类中几乎不出现,这样的词却能够很好代表这个类的特征,而TF-IDF不能区分这两种情况。
2)没有考虑特征词在类内部文档中的分布情况。在类内部的文档中,如果特征词均匀分布在其中,则这个特征词能够很好的代表这个类的特征,如果只在几篇文档中出现,而在此类的其它文档中不出现,显然这样的特征词不能够代表这个类的特征。
特征提取的目的在于降维。即使随机选取一部分词,分类效果也不会差到惊人的地步。采用了TF-IDF方法的分类效果当然也能有不错的效果。当然,TF-IDF用于向量空间模型,进行文档相似度计算是相当有效的。
2.卡方检验(Chi-square)
卡方检验最基本的思想就是通过观察实际值与理论值的偏差来确定理论的正确与否。具体做的时候常常先假设两个变量确实是独立的(“原假设”),然后观察实际值(观察值)与理论值(这个理论值是指“如果两者确实独立”的情况下应该有的值)的偏差程度,如果偏差足够小,我们就认为误差是很自然的样本误差,是测量手段不够精确导致或者偶然发生的,两者确确实实是独立的,此时就接受原假设;如果偏差大到一定程度,使得这样的误差不太可能是偶然产生或者测量不精确所致,我们就认为两者实际上是相关的,即否定原假设,而接受备择假设。理论值为E,实际值为x,偏差程度的计算公式为:

这个式子就是卡方检验使用的差值衡量公式。当提供了数个样本的观察值x1,x2,……xi,……xn之后,代入到式中就可以求得开方值,用这个值与事先设定的阈值比较,如果大于阈值(即偏差很大),就认为原假设不成立,反之则认为原假设成立。
在文本分类的特征选择阶段,一般使用“词t与类别c不相关”来做原假设,计算出的开方值越大,说明对原假设的偏离越大,我们越倾向于认为原假设的反面情况是正确的。选择的过程为每个词计算它与类别c的开方值,从大到小排个序(此时开方值越大越相关),取前k个就可以。
例如,N篇文档,分类有体育和非体育,考察特征词“篮球”与类别“体育”的相关性。
| 特征选择 | 1.属于“体育” | 2.不属于“体育” | 总 |
| 1.包含“篮球” | A | B | A+B |
| 2.不包含“篮球” | C | D | C+D |
| 总 | A+C | B+D | |
根据原假设,“体育”类别中包含“篮球”的文档比例应与所有文档中包含“篮球”的文档比例相同。故A的理论值应为:

差值:

同样计算剩下三种情况的差值D12,D21,D22。最后计算“篮球”与“体育”类文章的开方值:

进一步化简,注意如果给定了一个文档集合(例如我们的训练集)和一个类别,则N,M,N-M(即A+C和B+D)对同一类别文档中的所有词来说都是一样的,而我们只关心一堆词对某个类别的开方值的大小顺序,而并不关心具体的值,因此把它们去掉是完全可以的,故实际计算的时候我们都使用

卡方检验的缺点是:它只统计文档是否出现词,而不管出现了几次。这会使得他对低频词有所偏袒(因为它夸大了低频词的作用)。这就是开方检验著名的“低频词缺陷”。因此卡方检验也经常同其他因素如词频综合考虑来扬长避短。
3.信息增益
信息熵(信息量)(系统的)

意思就是一个变量可能的变化越多(反而跟变量具体的取值没有任何关系,只和值的种类多少以及发生概率有关),它携带的信息量就越大。
一个系一个特征t,系统有它和没它的时候信息量各是多少,两者的差值就是这个特征给系统带来的信息量统越是有序,信息熵就越低;反之,一个系统越乱,信息熵就越高。所以,信息熵也可以说是系统有序化程度的一个衡量。
信息增益(特征的)是指期望信息或者信息熵的有效减少量。
对于一个特征t,系统有它和没它的时候信息量各是多少,两者的差值就是这个特征给系统带来的信息量。有它即信息熵,无它则是条件熵。
条件熵:计算当一个特征t不能变化时,系统的信息量是多少。
对于一个特征X,它可能的取值有n多种(x1,x2,……,xn),计算每个值的条件熵,再取平均值。

在文本分类中,特征词t的取值只有t(代表t出现)和![]() (代表t不出现)。那么
(代表t不出现)。那么

最后,信息增益

但信息增益最大的问题还在于它只能考察特征对整个系统的贡献,而不能具体到某个类别上,这就使得它只适合用来做所谓“全局”的特征选择(指所有的类都使用相同的特征集合),而无法做“本地”的特征选择(每个类别有自己的特征集合,因为有的词,对这个类别很有区分度,对另一个类别则无足轻重)。
4.特征提取步骤
1. 卡方检验
1.1
1.2
1.3 计算每个词的卡方值,公式如下:

1.4
2. 信息增益
2.1
2.2
2.3

2.4

2.5
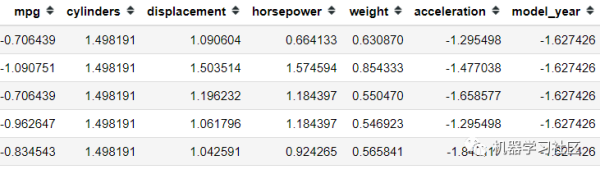
特征向量归一化方法
1、线性函数转换,表达式如下:
y=(x-MinValue)/(MaxValue-MinValue)
2、对数函数转换,表达式如下:
y=log10 (x)
3、反余切函数转换 ,表达式如下:
y=arctan(x)*2/PI
4、减去均值,乘以方差:
y=(x-means)/ variance