坊间常说:“数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已”。由此可见,特征工程在机器学习中占有相当重要的地位。在实际应用当中,可以说特征工程是机器学习成功的关键。
首先,从特征开始说起,假设你现在有一个标准的Excel表格数据,它的每一行表示的是一个观测样本数据,表格数据中的每一列就是一个特征。在这些特征中,有的特征携带的信息量丰富,有的(或许很少)则属于无关数据(irrelevant data),我们可以通过特征项和类别项之间的相关性(特征重要性)来衡量。比如,在实际应用中,常用的方法就是使用一些评价指标单独地计算出单个特征跟类别变量之间的关系。如Pearson相关系数,Gini-index(基尼指数),IG(信息增益)等。
其中,x属于X,X表一个特征的多个观测值,y表示这个特征观测值对应的类别列表。
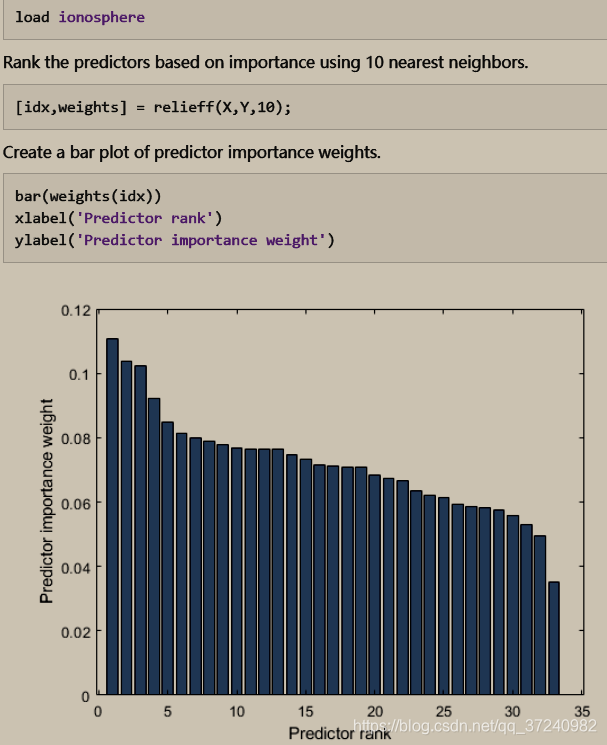
Pearson相关系数的取值在0到1之间,如果你使用这个评价指标来计算所有特征和类别标号的相关性,那么得到这些相关性之后,你可以将它们从高到低进行排名,然后选择一个子集作为特征子集(比如top 10%),接着用这些特征进行训练,看看性能如何。此外,你还可以画出不同子集的一个精度图,根据绘制的图形来找出性能最好的一组特征。
特征选择,它的目的是从特征集合中挑选一组最具统计意义的特征子集,从而达到降维的效果。
特征选择算法分类:过滤式,包裹式,嵌入式。这三类算法的区别主要在于学习算法在分析和选择特征的过程中发挥了怎样的作用。
- 过滤式: filter主要是通过给每个特征计算一个分数,然后按分数排序,从而选择top-k的特征作为新的特征集。他的优点很明显:计算速度快;缺点也很明显:没有考虑特征间的关系,导致效果不一定好。常见的fiter方法有: mutual information(互信息)、pearson相关系数、 卡方检验、 InfoGain等。基本原理如下图所示:
- 包裹式: 包装法特征选择方法直接把最终将要使用的学习器的性能作为特征子集的评价准则,这是与过滤法特征选择方法最大的区别。
filter: 特征是被提前选定的仅通过数据间的本质特性,并未进行学习算法的运算。简而言之,过滤式方法其先对数据集进行特征选择,使用选择出来的特征子集训练学习器,特征选择选择过程与后续的学习器无关。最简单的filter主要是通过给每个特征计算一个分数,然后按分数排序,从而选择得分最高的k个特征作为新的特征集。他的优点很明显:计算速度快;缺点也很明显:没有考虑特征间的关系,导致效果不一定好。常见的fiter方法有: mutual information(互信息)、pearson相关系数、 卡方检验、 InfoGain等。
wrapper:wrapper 使用预测模型来对特征集进行评分。也就是说,对每一个特征子集,我们进行训练并预测,得到的误差作为这个模型的分数(当然是越小越好了)。但是这种方法计算极慢,因为要考虑每一个feature subset。所以有时候,我们会用一些greedy的策略,例如我们所熟知的逐步回归的思想-逐步加入或者逐步删去。
embedded:embedded的方法都是内嵌在模型构建的本事的。事实上,这种特征选择的办法,都是基于构造机器学习模型时,产生的一些好的性质(比如线性回归时某些属性的系数为0)。这种办法属于比较常见的办法有:加入L1惩罚的回归模型(Lasso, SVM)、 随机森林(得到特征的importance)。embedded的计算复杂度介于上述两者之间。
学习器自身就有特征选择的能力。
过滤式方法通过一定的评价准则来分析特征,其目的是通过选择特征子集来优化准则函数,然而特征子集的选取有2^d种可能性,对于高维数据进行穷举搜索是不太现实的。为此,通常采用启发式搜索例如贪心算法、前项与后项搜索算法来替代穷举法,然而启发式搜索的方法会导致陷入局部最优解的情况。随机搜索方法例如遗传算法,通过在搜索过程中增加一定的随机性来避免陷入局部最优。
然而,在处理更高维的数据时,我们仅仅能进行单个特征的搜索,通过计算每一特征的重要程度并进行排列,选择得分最高的一部分作为特征子集,但这一方法的问题在于忽视了特征之间可能存在的相互关系。