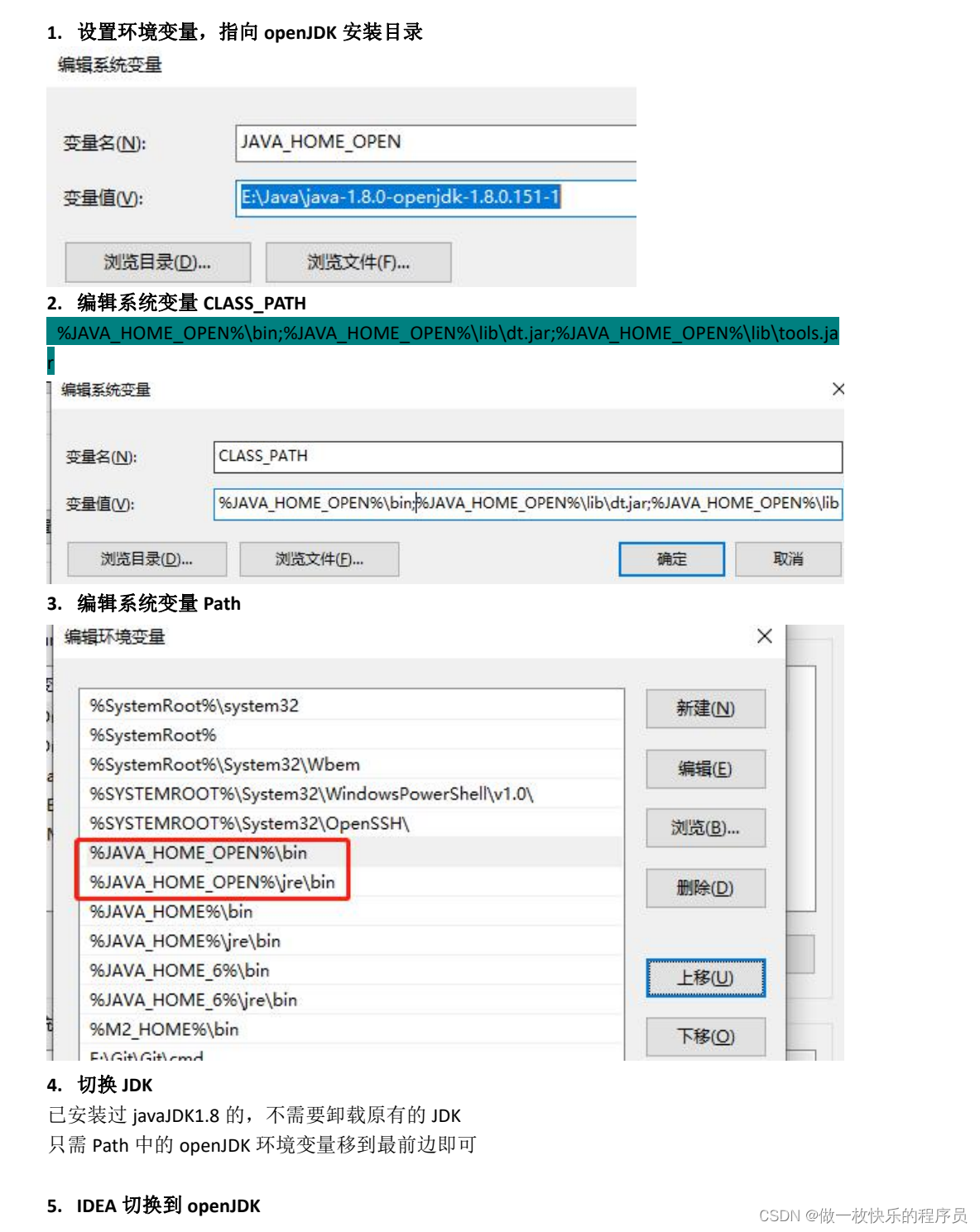
说明：

阅读本文前，请先阅读 参考网址1-基础使用 中的案例，本文适用于运行过 fmincon函数案例的读者！！！

一、fmincon函数：算法介绍

fmincon函数中，可以调用五种算法（具体每种算法的详细原理，可自行百度，如搜索“SQP算法原理”等），分别是：

‘interior-point’（默认！！！）：内点法
‘trust-region-reflective’：信赖域反射算法
‘sqp’：SQP算法
‘sqp-legacy’：（仅限于 optimoptions）
‘active-set’：活动集算法

一般情况下，默认采用的是内点法（interior-point），当然也可修改。
修改方法如下：

options = optimoptions('fmincon','Algorithm','interior-point'); 
[XXXXX]=fmincon( XXXXXXXXX,options);

添加“options ”项，并将Algorithm后的 interior-point 改为其余算法即可，如“sqp”。

这里着重声明一下内点法：
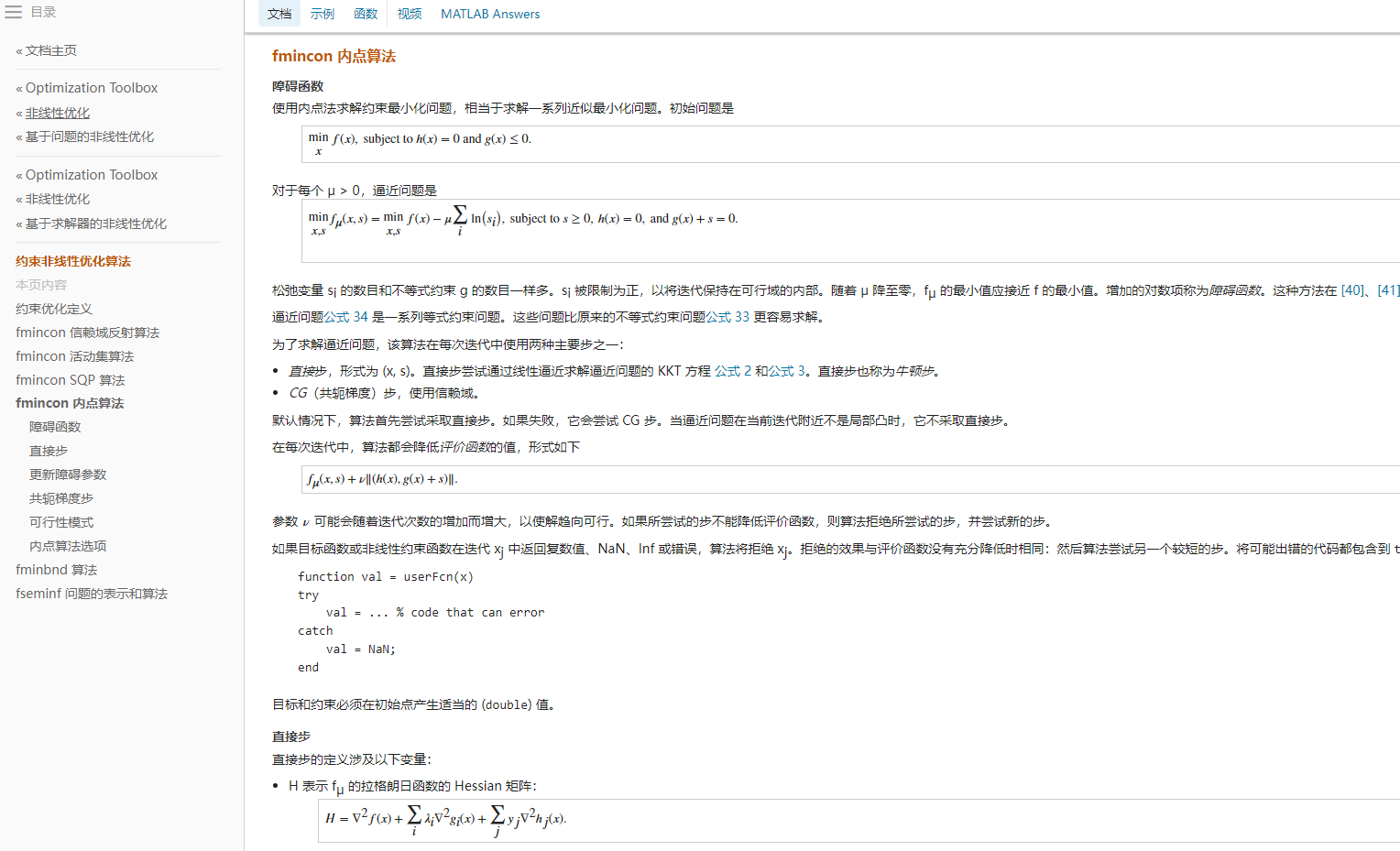
考虑到内点法一般有两种，一是障碍函数内点法，二是primal-Dual内点法（原对偶内点法）。根据“参考网址3”可知，fmincon函数采用的是前者——障碍函数内点法！而非原对偶内点法。截图如下：

二、fmincon函数：取消输出显示

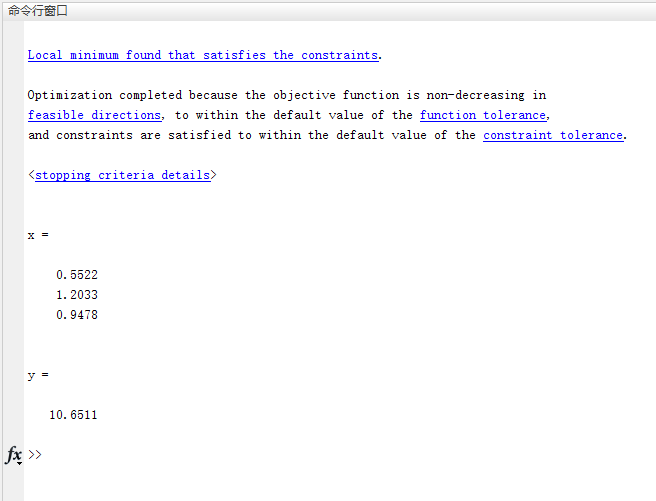
fmincon函数运行后，总会显示各种输出，如下图。尤其是fmincon函数在循环中的时候，这种输出尤为碍眼。因此，如何让fmincon函数不显示各种输出项？

方法：

options = optimoptions('fmincon','Display','notify'); 
[XXXXX]=fmincon( XXXXXXXXX,options);

添加“options ”项，并在Display后添加’notify’或’off’或’none’

详细信息见下图：（截图选自参考网址2 ）

三、fmincon函数：传递参数

使用句柄传参！否则无法实现参数传递。（句柄传参基础）

以参考网址1中的例子为例，我们向my_try_fun1.m函数中传递一个参数a写法如下：

function f = my_try_fun1(x,a)f=x(1).^2+x(2).^2+x(3).^2+a;

function [g,h]=my_try_fun2(x)g=[-x(1).^2+x(2)-x(3).^2x(1)+x(2).^2+x(3).^3-20];h=[-x(1)-x(2).^2+2x(2)+2*x(3).^2-3];

主函数为：

clear all
clcoptions = optimoptions('fmincon','Display','notify','Algorithm','interior-point');  %表示针对fmincon函数，Display一项选择notify，Algorithm一项选择interior-point。详见 https://ww2.mathworks.cn/help/optim/ug/fmincon.html#busow0w-1 a = 8 ; 
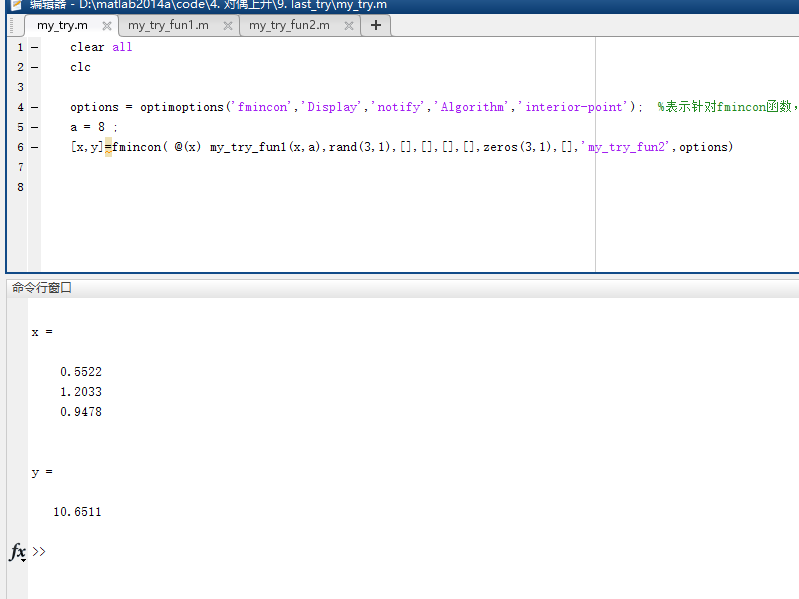
[x,y]=fmincon( @(x) my_try_fun1(x,a),rand(3,1),[],[],[],[],zeros(3,1),[],'my_try_fun2',options)

当然， my_try_fun2 函数若要传递参数，也可按照 my_try_fun1 的句柄方法书写，同理。

运行结果：

四、fmincon函数：非线性约束函数

非线性约束函数必须返回两个输出。
第一个输出对应于非线性不等式，第二个输出对应于非线性等式。

因此，前述 ‘my_try_fun2’ 约束中才会返回两个输出 g 与 h 。（ [g,h]=my_try_fun2(x) ）
当然了，若是没有非线性等式约束，则可写h = [ ]; 即可，但不可不写 h，因为非线性约束函数必须返回两个输出！
如：将前述的 my_try_fun2.m 函数改为下式：

function [g,h]=my_try_fun2(x)g=[-x(1).^2+x(2)-x(3).^2x(1)+x(2).^2+x(3).^3-20];h=[];

五、fmincon函数：迭代参数设置

1）如果迭代提前终止，可增大函数计算的最大次数

如下图，表示迭代超过了允许的默认设置中的函数计算的最大次数（对应名称为 MaxFunEvals ）！

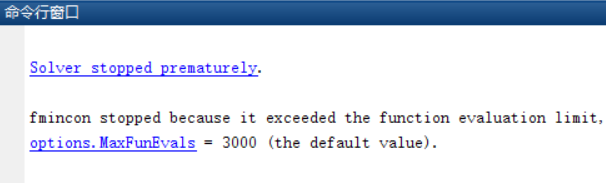
默认的函数计算的最大次数是3000次，因此，上调即可。我改为了100000。修改方法如下：

options = optimoptions('fmincon','MaxFunEvals',100000);

2）如果迭代时间太长，可降低迭代的精度

一阶最优性的终止容差（正标量）
默认值为 1e-6，名称是 TolFun，修改犯法如下：

options = optimoptions('fmincon','TolFun',10^(-2));

容差（停止条件）（标量）
针对内点法及SQP方法才可设置此项，名称是 ObjectiveLimit，默认值为 -1e20。如果目标函数值低于 ObjectiveLimit 并且迭代可行。（标注：这里的“迭代可行”应该指的是迭代至可行域内吧？），则迭代停止，因为问题很可能是无界的。修改方法如下：

options = optimoptions('fmincon','ObjectiveLimit',10^(-3));

3）如果不知迭代进展，可作图查看迭代实时进度

案例：

options = optimoptions('fmincon','PlotFcns','optimplotfval');

结果显示：

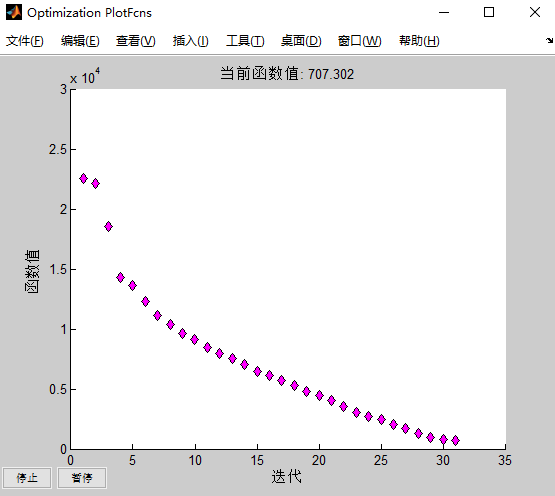
五、fmincon函数：内点法的 Hessian 矩阵近似算法选取

适用于 fmincon 内点算法的 Hessian 矩阵

六、fmincon函数：内点法的 Hessian 矩阵输入

求解器使用逼近的 Hessian 矩阵，它可能与真实的 Hessian 矩阵相差甚远。所以，为了稳定性及准确性，可人为输入 Hessian 矩阵。

参考网址5

参考网址6

参考网址7（主要网址）

下图以求解 Rosenbrock函数为例，展示如何书写 Hessian 矩阵，并给出函数调用时，出现的问题。

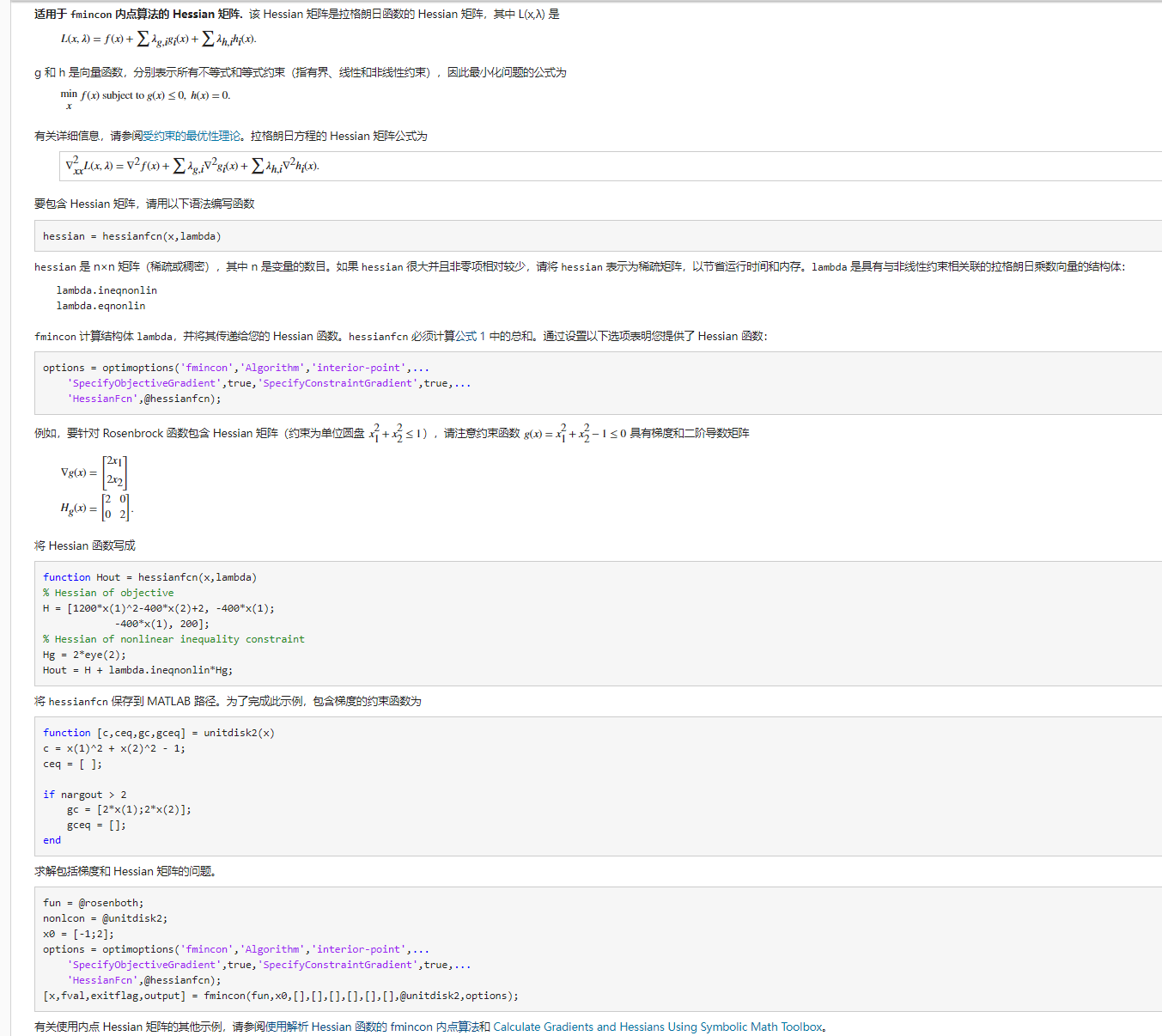
直接调用上述函数后，报错。错误信息如下：

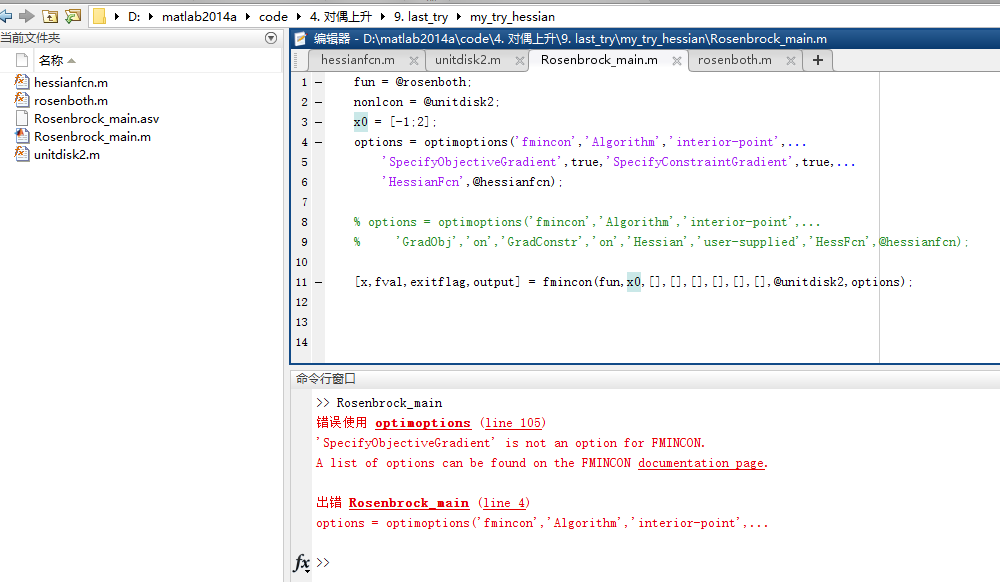
点击报错信息中的 “documentation page”，查阅错误原因。得知：是MATLAB版本差异导致的。在本人使用的 MATLAB 2014a 中，函数信息不含“SpecifyObjectiveGradient”等选项。

继而查阅新旧名称得知（参考网址8），名称发生了变化，因此，修改名称即可！

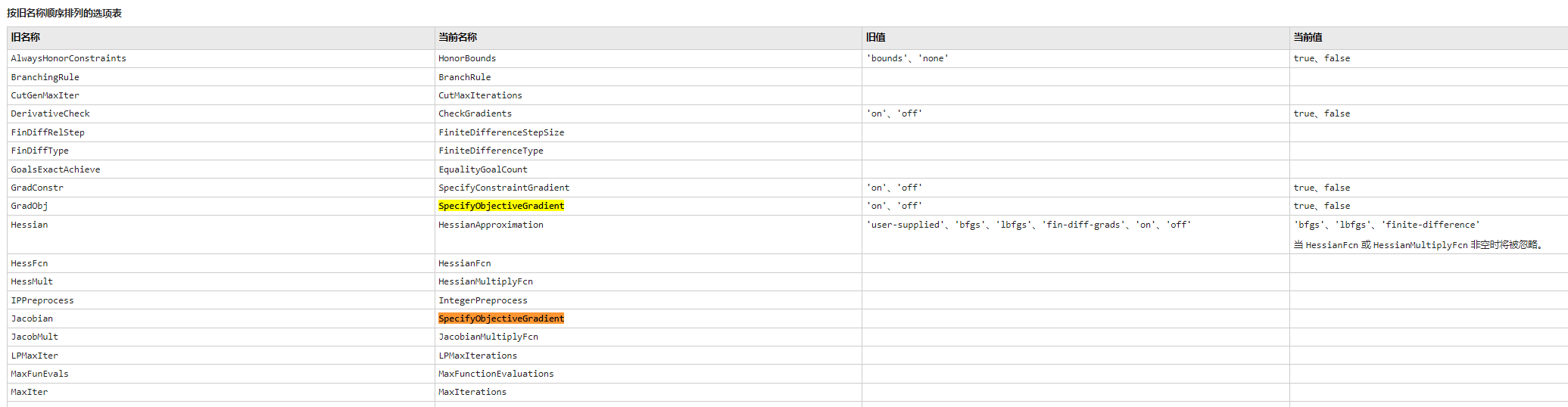
因此，只需要替换新旧名称即可！

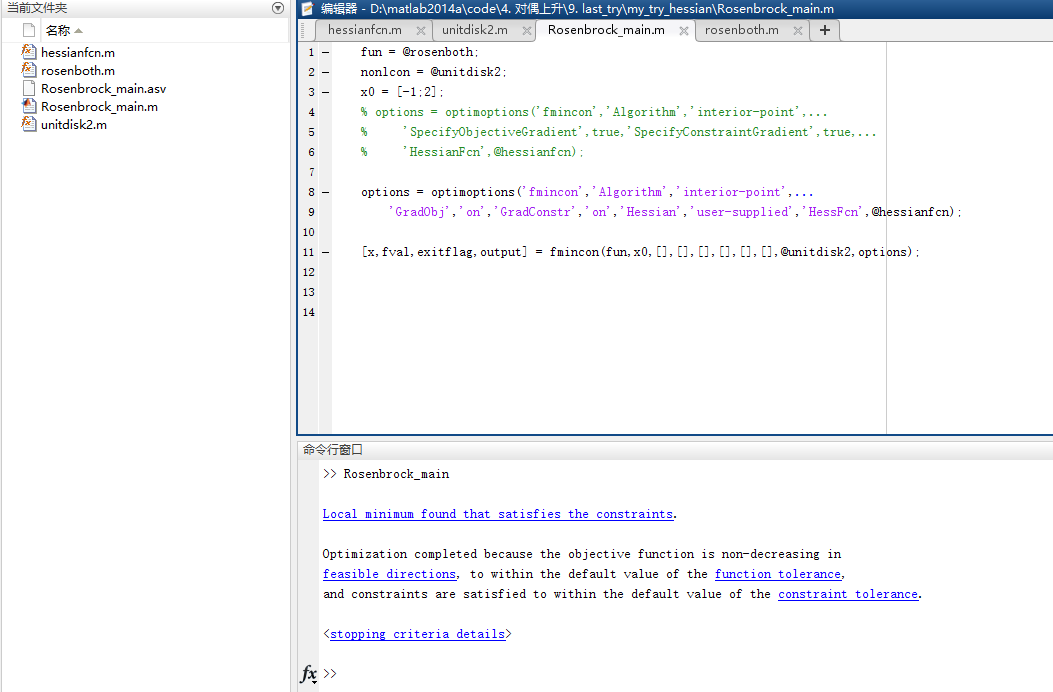
code 如下：

（1）主函数如下：

fun = @rosenboth;
nonlcon = @unitdisk2;
x0 = [-1;2];
% options = optimoptions('fmincon','Algorithm','interior-point',...
%     'SpecifyObjectiveGradient',true,'SpecifyConstraintGradient',true,...
%     'HessianFcn',@hessianfcn);options = optimoptions('fmincon','Algorithm','interior-point',...'GradObj','on','GradConstr','on','Hessian','user-supplied','HessFcn',@hessianfcn);[x,fval,exitflag,output] = fmincon(fun,x0,[],[],[],[],[],[],@unitdisk2,options);

（2）目标函数如下：（包含原始原始目标函数、目标函数梯度矩阵、目标函数Hessian矩阵）

function [f, g, H] = rosenboth(x)
% Calculate objective f
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;
g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));200*(x(2)-x(1)^2)];
H = [1200*x(1)^2-400*x(2)+2, -400*x(1);-400*x(1), 200];  % if nargout > 1 % gradient required
%     g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
%         200*(x(2)-x(1)^2)];
%     
%     if nargout > 2 % Hessian required
%         H = [1200*x(1)^2-400*x(2)+2, -400*x(1);
%             -400*x(1), 200];  
%     end
% 
% end

（注意：该函数不是仅有目标函数 f ！因为主函数的 options 中，设置了’GradObj’,‘on’。因此，目标函数中，除了原始目标函数以外，还必须有梯度及Hessian信息。）

（3）约束函数如下：（包含原始不等式约束函数c、原始等式约束函数ceq、不等式约束函数的梯度矩阵gc、等式约束函数的梯度矩阵gceq）

function [c,ceq,gc,gceq] = unitdisk2(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];
gc = [2*x(1);2*x(2)];
gceq = [];% if nargout > 2
%     gc = [2*x(1);2*x(2)];
%     gceq = [];
% end

（同理：该函数不是仅有约束函数 c 及 ceq （其中，c为不等式约束，ceq为等式约束）。因为主函数的 options 中，设置了’GradConstr’,‘on’。因此，约束函数中，除了原始约束函数以外，还必须有梯度信息。注：此处不需要Hessian信息，只写梯度即可，因为约束的Hessian矩阵写在另一个函数中了）

（4）拉格朗日函数的Hessian函数如下：（包含：目标函数Hessian矩阵H、约束函数Hessian矩阵Hg）

function Hout = hessianfcn(x,lambda)
% Hessian of objective
H = [1200*x(1)^2-400*x(2)+2, -400*x(1);-400*x(1), 200];
% Hessian of nonlinear inequality constraint
Hg = 2*eye(2);
Hout = H + lambda.ineqnonlin*Hg;