用Python进行多元线性回归分析（附代码）

https://developer.51cto.com/art/202008/624683.htm

很多人在做数据分析时会经常用到一元线性回归，这是描述两个变量间统计关系的最简单的回归模型。但现实问题中，我们往往会碰到多个变量间的线性关系的问题，这时就要用到多元线性回归，多元线性回归是一元回归的一种推广，其在实际应用中非常广泛，本文就用python代码来展示一下如何用多元线性回归来解决实际问题。

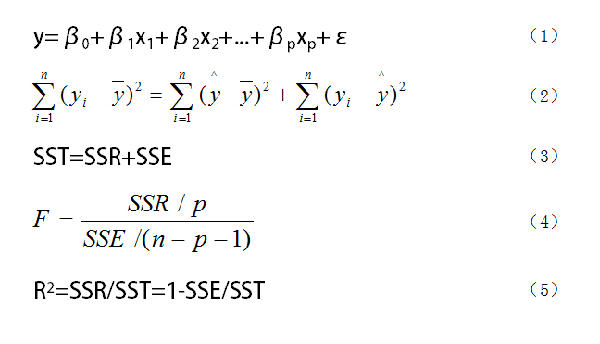
图1. 多元回归模型中要用到的公式

如图1所示，我们假设随机变量y与一般变量x1、x2、...、xp之间线性回归模型为（1）式，式中y为因变量，x1、x2、...、xp是自变量，β1、β2、...、βp是回归系数，β0是回归常数。对于一个实际问题，如果我们获得n组观测数据（xi1，xi2，...，xip；y）（i = 1，2，...，n），则我们可以把这n组观测数据写成矩阵形式y=Xβ+ε。

在求出了回归方程之后，我们往往还要对回归方程进行显著性检验。这里的显著性检验主要包括三部分。第一个是F检验，也就是检验自变量x1、x2、...、xp从整体上对y是否有明显的影响，主要用到（2）、（3）、（4）式，其中（2）和（3）式是一个式子，不过是用不同符号表示；第二个是t检验，是对每个自变量进行显著性检验，就是看每个自变量是否对y有显著性影响，这和前面从整体上检验还是有区别的；第三个是拟合优度，也就是R2，其取值在0到1之间，越接近1，表明回归拟合的效果越好，越接近于0，则效果越差，但R只能直观反映拟合的效果，不能代替F检验作为严格的显著性检验。

上面是多元线性回归的一个简单介绍，其详细原理内容较多，有兴趣的读者可以去查阅一下相关文献，这里不再赘述，只重点讲解如何用python进行分析。下面我们还是用代码来展示一下多元线性回归的分析过程。

这里我们用到的数据来源于2013年《中国统计年鉴》，数据以居民的消费性支出为因变量y，其他9个变量为自变量，其中x1是居民的食品花费，x2是衣着花费，x3是居住花费，x4是医疗保健花费，x5是文教娱乐花费，x6是职工平均工资，x7是地区的人均GDP，x8是地区的消费价格指数，x9是地区的失业率。在这所有变量里面，x1至x7以及y的单位是元，x9是百分数，x8没有单位，因为其是消费价格指数。数据的总体大小为31x10，即31行、10列，大体内容如图2所示。

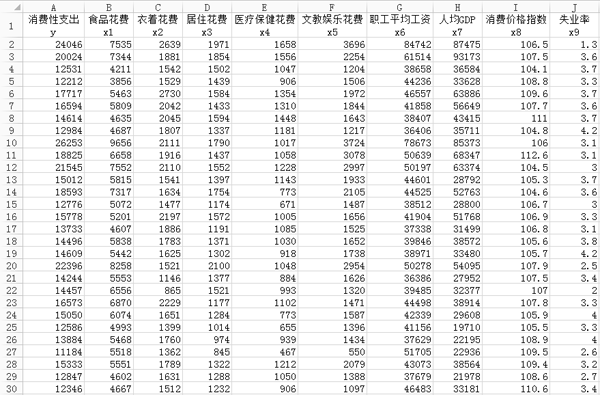
图2. 数据集部分内容

首先还是导入需要的库。

import numpy as np
import pandas as pd
import statsmodels.api as sm

接下来是数据预处理，因为原数据的列标太长，我们要处理一下，去除其中的中文，只留下英文名称。

file = r'C:\Users\data.xlsx'
data = pd.read_excel(file)
data.columns = ['y', 'x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9']

然后我们就开始生成多元线性模型，代码如下。

x = sm.add_constant(data.iloc[:,1:]) #生成自变量
y = data['y'] #生成因变量
model = sm.OLS(y, x) #生成模型
result = model.fit() #模型拟合
result.summary() #模型描述

很明显，这里的自变量是指x1到x9这9个自变量，代码data.iloc[:,1:]就是去掉原数据中第一列，也就是y那一列的数据，result.summary()则是生成一份结果描述，其内容如图3所示。

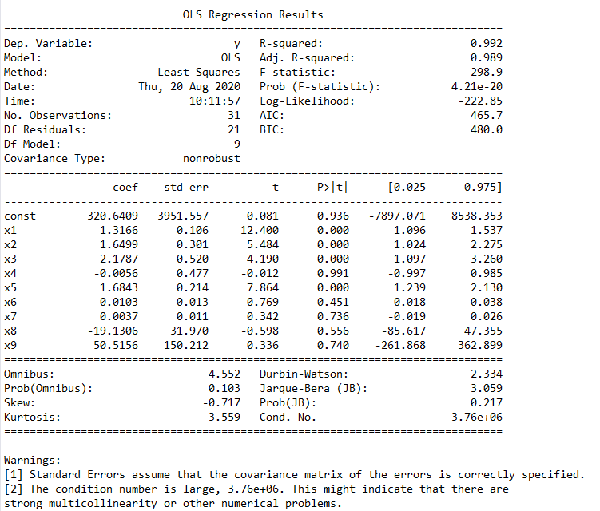
图3. 包含所有自变量的回归结果

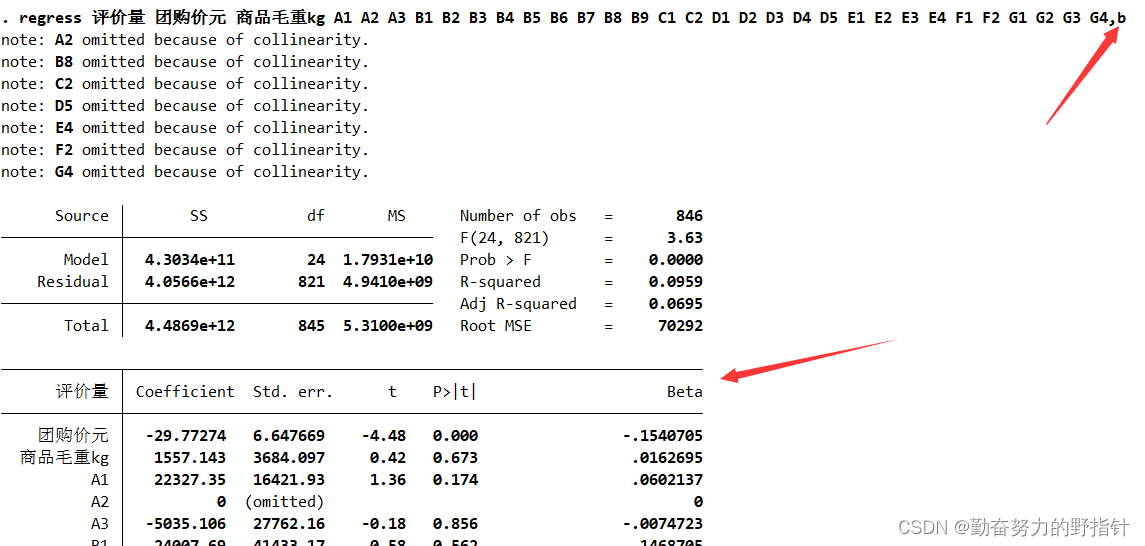
在这个结果中，我们主要看“coef”、“t”和“P>|t|”这三列。coef就是前面说过的回归系数，const这个值就是回归常数，所以我们得到的这个回归模型就是y = 320.640948 + 1.316588 x1 + 1.649859 x2 + 2.17866 x3 - 0.005609 x4 + 1.684283 x5 + 0.01032 x6 + 0.003655 x7 -19.130576 x8 + 50.515575 x9。而“t”和“P>|t|”这两列是等价的，使用时选择其中一个就行，其主要用来判断每个自变量和y的线性显著关系，后面我们会讲到。从图中还可以看出，Prob (F-statistic)为4.21e-20，这个值就是我们常用的P值，其接近于零，说明我们的多元线性方程是显著的，也就是y与x1、x2、...、x9有着显著的线性关系，而R-squared是0.992，也说明这个线性关系比较显著。理论上，这个多元线性方程已经求出来了，而且效果还不错，我们就可以用其进行预测了，但这里我们还是要进行更深一步的探讨。前面说过，y与x1、x2、...、x9有着显著的线性关系，这里要注意x1到x9这9个变量被看作是一个整体，y与这个整体有显著的线性关系，但不代表y与其中的每个自变量都有显著的线性关系，我们在这里要找出那些与y的线性关系不显著的自变量，然后把它们剔除，只留下关系显著的，这就是前面说过的t检验，t检验的原理内容有些复杂，有兴趣的读者可以自行查阅资料，这里不再赘述。我们可以通过图3中“P>|t|”这一列来判断，这一列中我们可以选定一个阈值，比如统计学常用的就是0.05、0.02或0.01，这里我们就用0.05，凡是P>|t|这列中数值大于0.05的自变量，我们都把它剔除掉，这些就是和y线性关系不显著的自变量，所以都舍去，请注意这里指的自变量是x1到x9，不包括图3中const这个值。但是这里有一个原则，就是一次只能剔除一个，剔除的这个往往是P值最大的那个，比如图3中P值最大的是x4，那么就把它剔除掉，然后再用剩下的x1、x2、x3、x5、x6、x7、x8、x9来重复上述建模过程，再找出P值最大的那个自变量，把它剔除，如此重复这个过程，直到所有P值都小于等于0.05，剩下的这些自变量就是我们需要的自变量，这些自变量和y的线性关系都比较显著，我们要用这些自变量来进行建模。

我们可以将上述过程写成一个函数，命名为looper，代码如下。

def looper(limit):
cols = ['x1', 'x2', 'x3', 'x5', 'x6', 'x7', 'x8', 'x9']
for i in range(len(cols)):
datadata1 = data[cols]
x = sm.add_constant(data1) #生成自变量
y = data['y'] #生成因变量
model = sm.OLS(y, x) #生成模型
result = model.fit() #模型拟合
pvalues = result.pvalues #得到结果中所有P值
pvalues.drop('const',inplace=True) #把const取得
pmax = max(pvalues) #选出最大的P值
if pmax>limit:
ind = pvalues.idxmax() #找出最大P值的index
cols.remove(ind) #把这个index从cols中删除
else:
return result
result = looper(0.05)
result.summary()

其结果如图4所示。从结果中可以看到最后剩下的有效变量为x1、x2、x3和x5，我们得到的多元线性模型为y = -1694.6269 + 1.3642 x1 + 1.7679 x2 + 2.2894 x3 + 1.7424 x5，这个就是我们最终要用到的有效的多元线性模型。

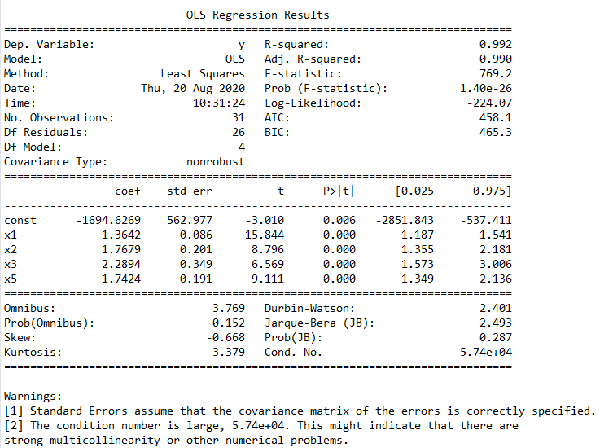
图4. 剔除无效变量后的回归模型

那么问题来了，前面我们得到的包含所有自变量的多元线性模型和这个剔除部分变量的模型，我们要选择哪一个，毕竟第一个模型的整体线性效果也挺显著，依据笔者的经验，这个还是要看具体的项目要求。因为我们实际项目中遇到的问题都是现实生活中真实存在的例子，不再是单纯的数学题了，比如本例中的x8消费价格指数和x9地区的失业率，这两个肯定对y是有一定影响的，如果盲目剔除，可能会对最终的结果产生不良影响，所以我们还是要根据实际需求来做决定。

最后还有一个问题要讨论一下，就是本例中没有对原始数据进行数据标准化。那么我们在数据分析中是否要对原始数据进行标准化？

这个也是要视情况而定。像本例中这些数据都是带有具体的量纲和单位，那么就不要对其进行标准化，我们得到的这个线性回归模型是在原始变量基础上进行拟合所得的结果，这个式子是包含物理单位的，说白了它们都是有一定实际意义的。在这种情况下，我们输入特定的自变量的值，即可得到相应的y值，预测效果直截了当，这是采取原始数据进行线性拟合的好处。

如果我们对原始数据采取了标准化处理，情况就不同了。标准化处理后自变量、因变量的物理单位没有了，我们拿此时的模型做预测时就会十分麻烦，要对新的自变量取值进行标准化，得到的y还是一个标准化后的数据，一眼看不到它的实际大小和物理意义。当然有些纯数学问题，其变量没有单位，这时候可以对其进行标准化，这会有利于对问题的分析。所以这个还是要视情况而定。