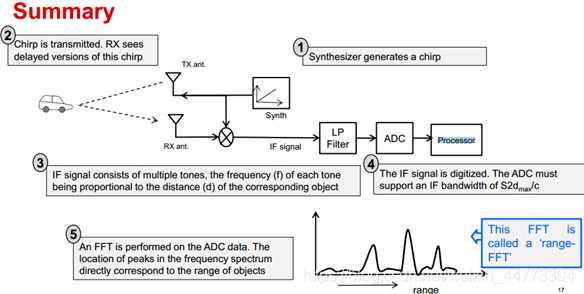
在与测距相关的应用中,雷达一般工作在FMCW模式,其原理是将经过调制的连续波信号以较高的载频发射出去,遇到被测目标时,将接收到的回波信号与当下发射的高频信号进行混频得到差频信号。对于线性调频来说,差频的频率即携带着目标的距离信息
雷达和测量目标相对静止
当雷达和测量目标相对静止,回波信号和发射信号相比,在时间上延迟了 τ \tau τ,可表示为:
τ = 2 R c \tau =\frac{2R}{c} τ=c2R
其中,R为雷达与目标物体的距离,c为光速。
下图为发射信号与回波信号的简化模型图。其中实线部分为发射信号频率曲线 f t f_{t} ft,虚线部分为回波信号频率曲线 f r f_{r} fr,混频输出的差频信号频率 f b f_{b} fb为发射信号和回波信号的频率差.
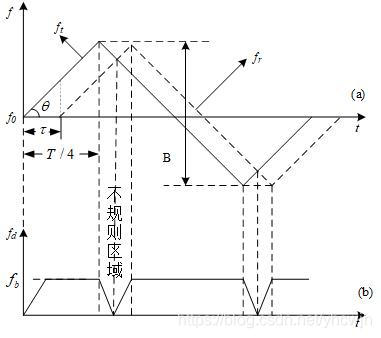
从图中可以得到
tan θ = B / 2 T / 4 = f b τ \tan \theta =\frac{B/2}{T/4}=\frac{{{f}_{b}}}{\tau } tanθ=T/4B/2=τfb
可以得到目标物体的距离值R、差频 f b f_{b} fb、调频带宽B、调制周期T之间的关系:
R = c T 4 B f b R=\frac{cT}{4B}{{f}_{b}} R=4BcTfb
当三角波周期T和带宽B为固定的值时,在雷达与目标相对静止时,目标距离与差频 f b f_{b} fb成正比。因此,可以通过对差频信号 f b f_{b} fb的检测来获取目标距离R。
雷达和测量目标之间存在相对运动
多普勒效应指出,波在波源向观察者接近时接收频率变高,而在波源远离观察者时接收频率变低。当观察者移动时也能得到同样的结论。同理,用雷达观测运动目标时也会存在多普勒效应:当目标接近雷达时,雷达的接收频率变高;当目标远离雷达时,雷达的接收频率会变低。
假设雷达和目标接近,在回波信号中包含着由于目标的运动带来的多普勒频移 f d f_{d} fd信号。可以得出在三角波的上升沿和下降沿差频信号的频率可分别表示如下:
f b + = f b − f d {{f}_{b+}}={{f}_{b}}-{{f}_{d}} fb+=fb−fd
f b − = f b + f d {{f}_{b-}}={{f}_{b}}+{{f}_{d}} fb−=fb+fd
其中, f b f_{b} fb为雷达和目标物体是相对静止时的差频信号的频率,而 f d f_{d} fd为目标运动带来的多普勒频移信号。根据多普勒原理,多普勒频移 f d f_{d} fd可以表示为
f d = 2 f 0 v c {{f}_{d}}=\frac{2{{f}_{0}}v}{c} fd=c2f0v
其中, f 0 f_{0} f0为发射信号中心频率。
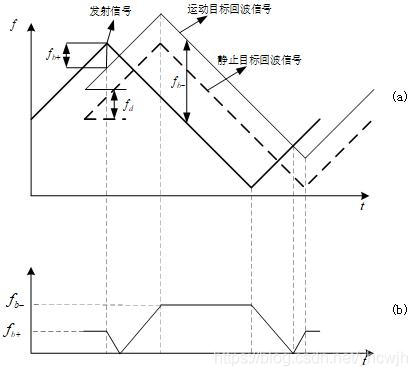
上图为雷达与目标存在相对运动时的(a)发射信号与回波信号(b)差频信号
可以得到三角波上升沿所对应的差频 f b + {{f}_{b+}} fb+和三角波下降沿所对应的差频 f b − {{f}_{b-}} fb−:
f b + = 4 B R c T − 2 f 0 v c {{f}_{b+}}=\frac{4BR}{cT}-\frac{2{{f}_{0}}v}{c} fb+=cT4BR−c2f0v
f b − = 4 B R c T + 2 f 0 v c {{f}_{b-}}=\frac{4BR}{cT}+\frac{2{{f}_{0}}v}{c} fb−=cT4BR+c2f0v
则目标距离和速度的表达式为
R = c T 8 B ( f b − + f b + ) R=\frac{cT}{8B}\left( {{f}_{b-}}+{{f}_{b+}} \right) R=8BcT(fb−+fb+)
v = c 4 f 0 ( f b − − f b + ) v=\frac{c}{4{{f}_{0}}}\left( {{f}_{b-}}-{{f}_{b+}} \right) v=4f0c(fb−−fb+)
因此,可以通过 f b + {{f}_{b+}} fb+和 f b − {{f}_{b-}} fb−来计算距离 R R R和速度 v v v的值
单个静止目标回波信号的时域-频域分析
对于同一时刻,在三角波的上升沿,回波信号的频率低于发射信号的频率。在三角波的下降沿,雷达回波信号的频率则会高于发射信号频率。所以,单个目标的差频信号会围绕着三角波的峰顶和峰谷处呈现对称形式。整个差频信号则是一个周期性信号,周期等于三角波的调制周期T。
设 x ( t ) x\left( t \right) x(t)为差频时域信号, s ( t ) s\left( t \right) s(t)为三角波上升沿所对应的差频时域信号,则三角波下降沿所对应的差频时域信号为 s ( T − t ) s\left( T-t \right) s(T−t)。对差频信号进行时域数学建模,即
x ( t ) = { s ( t ) , t ∈ [ 0 , T 2 ] + n T , n = 0 , 1 , 2... s ( T − t ) , t ∈ [ T 2 , T ] + n T , n = 0 , 1 , 2... x\left( t \right)=\left\{ \begin{aligned} & s\left( t \right),\ \ \ \ \ \ \ \ \ \ \ t\in \left[ 0,\frac{T}{2} \right]+nT,n=0,1,2... \\ & s\left( T-t \right)\ ,\ \ t\ \in \left[ \frac{T}{2},T \right]\ +nT,n=0,1,2... \\ \end{aligned} \right. x(t)=⎩⎪⎪⎪⎨⎪⎪⎪⎧s(t), t∈[0,2T]+nT,n=0,1,2...s(T−t) , t ∈[2T,T] +nT,n=0,1,2...
由于差频信号是周期信号,周期信号可以展开成傅里叶级数的形式
x ( t ) = ∑ k = - ∞ ∞ A k e j k Ω T t x\left( t \right)=\sum\limits_{k=\text{-}\infty }^{\infty }{{{A}_{k}}}{{e}^{jk{{\Omega }_{T}}t}} x(t)=k=-∞∑∞AkejkΩTt
其中, Ω T = 2 π T {{\Omega }_{T}}=\frac{2\pi }{T} ΩT=T2π, A k {{A}_{k}} Ak为傅里叶级数的系数。
系数 A k {{A}_{k}} Ak可以通过如下公式来求解
A k = 1 T ∫ 0 T x ( t ) e − j k Ω T t d t = 1 T ∫ 0 T 2 s ( t ) e − j k Ω T t d t + 1 T ∫ T 2 T s ( T − t ) e − j k Ω T t d t {{A}_{k}}=\frac{1}{T}\int_{0}^{T}{x\left( t \right)}{{e}^{-jk{{\Omega }_{T}}t}}dt=\frac{1}{T}\int_{0}^{\frac{T}{2}}{s\left( t \right)}{{e}^{-jk{{\Omega }_{T}}t}}dt+\frac{1}{T}\int_{\frac{T}{2}}^{T}{s\left( T-t \right)}{{e}^{-jk{{\Omega }_{T}}t}}dt Ak=T1∫0Tx(t)e−jkΩTtdt=T1∫02Ts(t)e−jkΩTtdt+T1∫2TTs(T−t)e−jkΩTtdt
对上式的第二项进行变量替换
1 T ∫ T 2 T s ( T − t ) e − j k Ω T t d t = t ′ = T − t − 1 T e − j k Ω T T ∫ T 2 0 s ( t ′ ) e j k Ω T t ′ d t ′ = t = t ′ − 1 T ∫ T 2 0 s ( t ) e j k Ω T t d t = 1 T ∫ 0 T 2 s ( t ) e j k Ω T t d t \begin{aligned} & \frac{1}{T}\int_{\frac{T}{2}}^{T}{s\left( T-t \right)}{{e}^{-jk{{\Omega }_{T}}t}}dt\overset{t'=T-t}{\mathop{=}}\,-\frac{1}{T}{{e}^{-jk{{\Omega }_{T}}T}}\int_{\frac{T}{2}}^{0}{s\left( t' \right)}{{e}^{jk{{\Omega }_{T}}t'}}dt' \\ & \overset{t=t'}{\mathop{=}}\,-\frac{1}{T}\int_{\frac{T}{2}}^{0}{s\left( t \right)}{{e}^{jk{{\Omega }_{T}}t}}dt=\frac{1}{T}\int_{0}^{\frac{T}{2}}{s\left( t \right)}{{e}^{jk{{\Omega }_{T}}t}}dt \\ \end{aligned} T1∫2TTs(T−t)e−jkΩTtdt=t′=T−t−T1e−jkΩTT∫2T0s(t′)ejkΩTt′dt′=t=t′−T1∫2T0s(t)ejkΩTtdt=T1∫02Ts(t)ejkΩTtdt
则
A k = 1 T ∫ 0 T 2 s ( t ) e − j k Ω T t d t + 1 T ∫ 0 T 2 s ( t ) e j k Ω T t d t = 1 T ∫ 0 T 2 s ( t ) e − j k Ω T t d t + 1 T ∫ 0 T 2 s ( t ) e − j ( − k Ω T ) t d t \begin{aligned} & {{A}_{k}}=\frac{1}{T}\int_{0}^{\frac{T}{2}}{s\left( t \right)}{{e}^{-jk{{\Omega }_{T}}t}}dt+\frac{1}{T}\int_{0}^{\frac{T}{2}}{s\left( t \right)}{{e}^{jk{{\Omega }_{T}}t}}dt \\ & =\frac{1}{T}\int_{0}^{\frac{T}{2}}{s\left( t \right)}{{e}^{-jk{{\Omega }_{T}}t}}dt+\frac{1}{T}\int_{0}^{\frac{T}{2}}{s\left( t \right)}{{e}^{-j\left( -k{{\Omega }_{T}} \right)t}}dt \\ \end{aligned} Ak=T1∫02Ts(t)e−jkΩTtdt+T1∫02Ts(t)ejkΩTtdt=T1∫02Ts(t)e−jkΩTtdt+T1∫02Ts(t)e−j(−kΩT)tdt
其中,第一项是信号 s ( t ) s\left( t \right) s(t)被时间窗口函数 R T / 2 = { 1 t ∈ [ 0 , T 2 ] 0 t ∈ o t h e r {{R}_{T/2}}=\left\{ \begin{aligned} & 1\ \ \ \ t\in \left[ 0,\frac{T}{2} \right] \\ & 0\ \ \ \ t\in other\\ \end{aligned} \right. RT/2=⎩⎪⎨⎪⎧1 t∈[0,2T]0 t∈other,然后信号做傅里叶变换在 Ω = k Ω T \Omega =k{{\Omega }_{T}} Ω=kΩT处取值的结果。第二项则是在 Ω = − k Ω T \Omega =-k{{\Omega }_{T}} Ω=−kΩT处取值的结果。
上式可以进一步表示为
A k = 1 T ∫ 0 T 2 s ( t ) e − j k Ω T t d t + 1 T ∫ 0 T 2 s ( t ) e j k Ω T t d t = 2 T ∫ 0 T 2 s ( t ) cos ( k Ω T t ) d t \begin{aligned} & {{A}_{k}}=\frac{1}{T}\int_{0}^{\frac{T}{2}}{s\left( t \right)}{{e}^{-jk{{\Omega }_{T}}t}}dt+\frac{1}{T}\int_{0}^{\frac{T}{2}}{s\left( t \right)}{{e}^{jk{{\Omega }_{T}}t}}dt \\ & =\frac{2}{T}\int_{0}^{\frac{T}{2}}{s\left( t \right)}\cos \left( k{{\Omega }_{T}}t \right)dt \\ \end{aligned} Ak=T1∫02Ts(t)e−jkΩTtdt+T1∫02Ts(t)ejkΩTtdt=T2∫02Ts(t)cos(kΩTt)dt
对于单个检测目标,设差频信号为单一频率的信号,则上升沿所对应的差频时域信号可表示为:
s ( t ) = cos ( 2 π f b t + φ ) = cos ( Ω b t + φ ) s\left( t \right)=\cos \left( 2\pi {{f}_{b}}t+\varphi \right)=\cos \left( {{\Omega }_{b}}t+\varphi \right) s(t)=cos(2πfbt+φ)=cos(Ωbt+φ)
其中, φ \varphi φ是相位, Ω b {{\Omega }_{b}} Ωb为差频信号 f b f_{b} fb所对应的模拟角频率。那么
A k = 2 T ∫ 0 T 2 cos ( k Ω T t ) cos ( Ω b t + φ ) d t = 1 T ∫ 0 T 2 cos [ ( k Ω T + Ω b ) t + φ ] d t + 1 T ∫ 0 T 2 cos [ ( k Ω T − Ω b ) t − φ ] d t = 1 T ( k Ω T + Ω b ) [ sin [ ( k Ω T + Ω b ) T 2 + φ ] − sin φ ] + 1 T ( k Ω T − Ω b ) [ sin [ ( k Ω T − Ω b ) T 2 − φ ] + sin φ ] \begin{aligned} & {{A}_{k}}=\frac{2}{T}\int_{0}^{\frac{T}{2}}{\cos \left( k{{\Omega }_{T}}t \right)\cos \left( {{\Omega }_{b}}t+\varphi \right)}dt \\ & =\frac{1}{T}\int_{0}^{\frac{T}{2}}{\cos \left[ \left( k{{\Omega }_{T}}+{{\Omega }_{b}} \right)t+\varphi \right]}dt+\frac{1}{T}\int_{0}^{\frac{T}{2}}{\cos \left[ \left( k{{\Omega }_{T}}-{{\Omega }_{b}} \right)t-\varphi \right]}dt \\ & \text{=}\frac{1}{T\left( k{{\Omega }_{T}}+{{\Omega }_{b}} \right)}\left[ \sin \left[ \left( k{{\Omega }_{T}}+{{\Omega }_{b}} \right)\frac{T}{2}+\varphi \right]-\sin \varphi \right] \\ & +\frac{1}{T\left( k{{\Omega }_{T}}-{{\Omega }_{b}} \right)}\left[ \sin \left[ \left( k{{\Omega }_{T}}-{{\Omega }_{b}} \right)\frac{T}{2}-\varphi \right]+\sin \varphi \right] \\ \end{aligned} Ak=T2∫02Tcos(kΩTt)cos(Ωbt+φ)dt=T1∫02Tcos[(kΩT+Ωb)t+φ]dt+T1∫02Tcos[(kΩT−Ωb)t−φ]dt=T(kΩT+Ωb)1[sin[(kΩT+Ωb)2T+φ]−sinφ]+T(kΩT−Ωb)1[sin[(kΩT−Ωb)2T−φ]+sinφ]
不妨设 φ = 0 \varphi \text{=}0 φ=0,则
A k = 1 2 sin [ ( k Ω T + Ω b ) T 2 ] ( k Ω T + Ω b ) T 2 + 1 2 sin [ ( k Ω T − Ω b ) T 2 ] ( k Ω T − Ω b ) T 2 = 1 2 sin [ ( Ω + Ω b ) T 2 ] ( Ω + Ω b ) T 2 ∣ Ω = k Ω T + 1 2 sin [ ( Ω − Ω b ) T 2 ] ( Ω − Ω b ) T 2 ∣ Ω = k Ω T \begin{aligned} & {{A}_{k}}=\frac{1}{2}\frac{\sin \left[ \left( k{{\Omega }_{T}}+{{\Omega }_{b}} \right)\frac{T}{2} \right]}{\left( k{{\Omega }_{T}}+{{\Omega }_{b}} \right)\frac{T}{2}}+\frac{1}{2}\frac{\sin \left[ \left( k{{\Omega }_{T}}-{{\Omega }_{b}} \right)\frac{T}{2} \right]}{\left( k{{\Omega }_{T}}-{{\Omega }_{b}} \right)\frac{T}{2}} \\ & ={{\left. \frac{1}{2}\frac{\sin \left[ \left( \Omega +{{\Omega }_{b}} \right)\frac{T}{2} \right]}{\left( \Omega +{{\Omega }_{b}} \right)\frac{T}{2}} \right|}_{\Omega =k{{\Omega }_{T}}}}+{{\left. \frac{1}{2}\frac{\sin \left[ \left( \Omega -{{\Omega }_{b}} \right)\frac{T}{2} \right]}{\left( \Omega -{{\Omega }_{b}} \right)\frac{T}{2}} \right|}_{\Omega =k{{\Omega }_{T}}}} \\ \end{aligned} Ak=21(kΩT+Ωb)2Tsin[(kΩT+Ωb)2T]+21(kΩT−Ωb)2Tsin[(kΩT−Ωb)2T]=21(Ω+Ωb)2Tsin[(Ω+Ωb)2T]∣∣∣∣∣Ω=kΩT+21(Ω−Ωb)2Tsin[(Ω−Ωb)2T]∣∣∣∣∣Ω=kΩT
可以看出,系数 A k {{A}_{k}} Ak呈现出辛格函数的包络形式。当 ( k Ω T − Ω b ) ⋅ T / 2 = m π , m = 0 , 1 , 2... \left( k{{\Omega }_{T}}-{{\Omega }_{b}} \right)\cdot T/2=m\pi ,m=0,1,2... (kΩT−Ωb)⋅T/2=mπ,m=0,1,2...时,或者 ( k Ω T + Ω b ) ⋅ T / 2 = m π , m = 0 , 1 , 2... \left( k{{\Omega }_{T}}+{{\Omega }_{b}} \right)\cdot T/2=m\pi ,m=0,1,2... (kΩT+Ωb)⋅T/2=mπ,m=0,1,2...时, A k = 0 {{A}_{k}}=0 Ak=0。
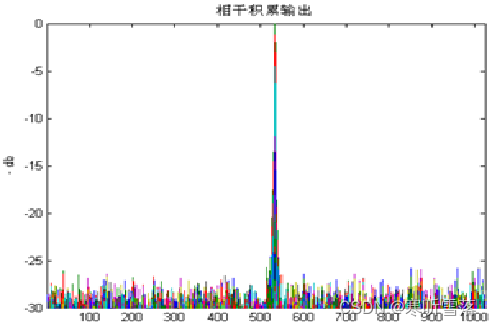
可以解得 Ω b = ( k − m ) Ω T {{\Omega }_{b}}=\left( k-m \right){{\Omega }_{T}} Ωb=(k−m)ΩT或 Ω b = ( m − k ) Ω T {{\Omega }_{b}}=\left( m-k \right){{\Omega }_{T}} Ωb=(m−k)ΩT时, A k = 0 {{A}_{k}}=0 Ak=0。当 Ω b > > Ω T {{\Omega }_{b}}>>{{\Omega }_{T}} Ωb>>ΩT时候, A k {{A}_{k}} Ak的数值大小的分布如下图所示

当 Ω b = k ⋅ Ω T {{\Omega }_{b}}=k\cdot {{\Omega }_{T}} Ωb=k⋅ΩT时, A k {{A}_{k}} Ak的大小分布如图中的黑色实线所示, Ω b {{\Omega }_{b}} Ωb恰好落在离散的整数频点上,其所对应的 A k {{A}_{k}} Ak为最大值。如果 Ω b {{\Omega }_{b}} Ωb落在两个离散的整数频点中间,如图中的红色虚线所示,相当于辛格函数的峰值落在了两个离散整数频点中间,且距离信号实际频率越近的频点 A k {{A}_{k}} Ak越大。
可以看出 A k {{A}_{k}} Ak的值的分布随着 Ω b {{\Omega }_{b}} Ωb的变化而变化,且包络呈现辛格函数的形状。因此,FMCW体制雷达的差频信号的傅里叶变换是一个傅里叶级数的形式,频谱上呈现离散状态,且可以通过找寻 A k {{A}_{k}} Ak的最大值来确定或者近似确定 Ω b {{\Omega }_{b}} Ωb的值。
雷达距离分辨率
当两个目标位于同一方位角,但与雷达的距离不同时,二者被雷达区分出来的最小距离称为距离分辨率。通常定义为:当较近目标回波脉冲的后沿(下降沿)与较远目标回波的前沿(上升沿)刚好重合时,作为可分辨的极限。此时两目标间的距离就是距离分辨率,常用 △ R \vartriangle R △R表示
Δ R = c T 4 B Δ f b \Delta R=\frac{cT}{4B}\Delta {{f}_{b}} ΔR=4BcTΔfb
其中, Δ f b \Delta {{f}_{b}} Δfb为差频分辨率。一般情况下,差频信号的周期应该小于三角波周期的一半,即
f b ≥ 2 T {{f}_{b}}\ge \frac{2}{T} fb≥T2
那么
Δ R ≥ c T 4 B ⋅ 2 T = c 2 B \Delta R\ge \frac{cT}{4B}\cdot \frac{2}{T}=\frac{c}{2B} ΔR≥4BcT⋅T2=2Bc
距离分辨率和系统的带宽B有关
雷达差频信号仿真
给出雷达差频信号的仿真,参数设置如下:
| 参数名称 | 参数值 |
|---|---|
| 三角板周期 | 1KHz |
| 采样频率 | 1MHz |
| 中心频率 | 20KHz |
| 调制带宽 | 2KHz |
可以得到三角波信号如下:
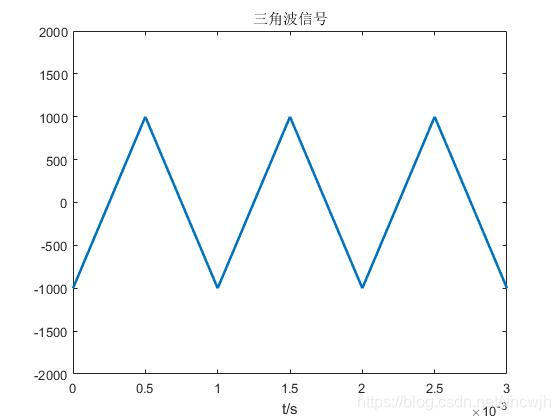
调制后的信号(发射信号为):
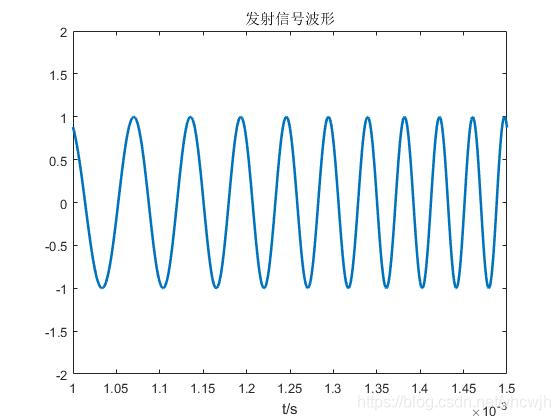
回波信号为:
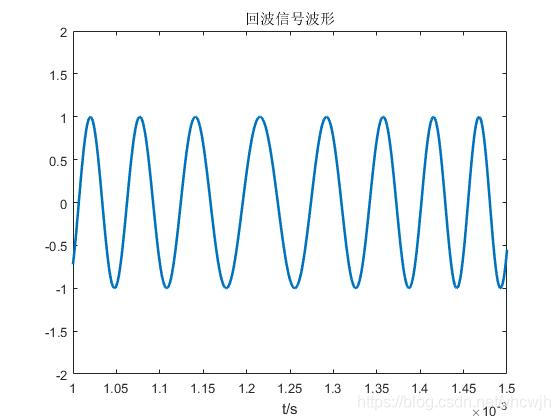
那么相应的差频信号,即实际低通滤波后的信号,可以表示为:
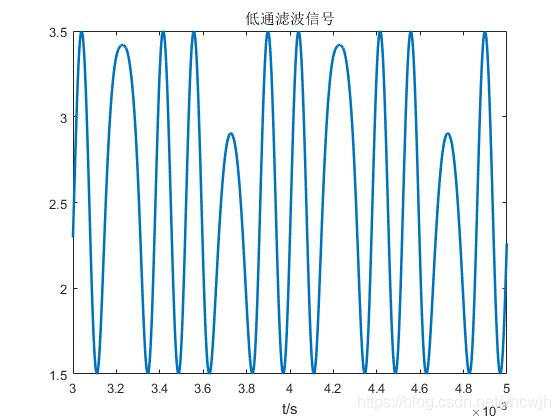
从仿真的结果也可以看出与上面的分析一致。