0. 简介

上一节我们将while内部的IKD-Tree部分全部讲完，下面将是最后一部分，关于后端优化更新的部分。

1. 迭代更新

最后一块主要做的就是，拿当前帧与IKD-Tree建立的地图算出的残差，然后去计算更新自己的位置，并将更新后的结果通过map_incremental函数插入到由ikd-Tree表示的映射中。

// 外参，旋转矩阵转欧拉角V3D ext_euler = SO3ToEuler(state_point.offset_R_L_I);fout_pre << setw(20) << Measures.lidar_beg_time - first_lidar_time << " " << euler_cur.transpose() << " " << state_point.pos.transpose() << " " << ext_euler.transpose() << " " << state_point.offset_T_L_I.transpose() << " " << state_point.vel.transpose()<< " " << state_point.bg.transpose() << " " << state_point.ba.transpose() << " " << state_point.grav << endl; //输出预测的结果if (0) // If you need to see map point, change to "if(1)"{// 释放PCL_Storage的内存PointVector().swap(ikdtree.PCL_Storage);// 把树展平用于展示ikdtree.flatten(ikdtree.Root_Node, ikdtree.PCL_Storage, NOT_RECORD);featsFromMap->clear();featsFromMap->points = ikdtree.PCL_Storage;}pointSearchInd_surf.resize(feats_down_size); //搜索索引Nearest_Points.resize(feats_down_size);      //将降采样处理后的点云用于搜索最近点int rematch_num = 0;bool nearest_search_en = true; //t2 = omp_get_wtime();/*** 迭代状态估计 ***/double t_update_start = omp_get_wtime();double solve_H_time = 0;//迭代卡尔曼滤波更新，更新地图信息kf.update_iterated_dyn_share_modified(LASER_POINT_COV, solve_H_time);state_point = kf.get_x();euler_cur = SO3ToEuler(state_point.rot);pos_lid = state_point.pos + state_point.rot * state_point.offset_T_L_I;geoQuat.x = state_point.rot.coeffs()[0];geoQuat.y = state_point.rot.coeffs()[1];geoQuat.z = state_point.rot.coeffs()[2];geoQuat.w = state_point.rot.coeffs()[3];double t_update_end = omp_get_wtime();/******* 发布里程计 *******/publish_odometry(pubOdomAftMapped);/*** 向映射kdtree添加特性点 ***/t3 = omp_get_wtime();map_incremental();t5 = omp_get_wtime();/******* 发布轨迹和点 *******/publish_path(pubPath);if (scan_pub_en || pcd_save_en)publish_frame_world(pubLaserCloudFull);if (scan_pub_en && scan_body_pub_en){publish_frame_body(pubLaserCloudFull_body);publish_frame_lidar(pubLaserCloudFull_lidar);}// publish_effect_world(pubLaserCloudEffect);// publish_map(pubLaserCloudMap);/*** Debug 参数 ***/if (runtime_pos_log){frame_num++;kdtree_size_end = ikdtree.size();aver_time_consu = aver_time_consu * (frame_num - 1) / frame_num + (t5 - t0) / frame_num;aver_time_icp = aver_time_icp * (frame_num - 1) / frame_num + (t_update_end - t_update_start) / frame_num;aver_time_match = aver_time_match * (frame_num - 1) / frame_num + (match_time) / frame_num;aver_time_incre = aver_time_incre * (frame_num - 1) / frame_num + (kdtree_incremental_time) / frame_num;aver_time_solve = aver_time_solve * (frame_num - 1) / frame_num + (solve_time + solve_H_time) / frame_num;aver_time_const_H_time = aver_time_const_H_time * (frame_num - 1) / frame_num + solve_time / frame_num;T1[time_log_counter] = Measures.lidar_beg_time;s_plot[time_log_counter] = t5 - t0;                         //整个流程总时间s_plot2[time_log_counter] = feats_undistort->points.size(); //特征点数量s_plot3[time_log_counter] = kdtree_incremental_time;        // kdtree增量时间s_plot4[time_log_counter] = kdtree_search_time;             // kdtree搜索耗时s_plot5[time_log_counter] = kdtree_delete_counter;          // kdtree删除点数量s_plot6[time_log_counter] = kdtree_delete_time;             // kdtree删除耗时s_plot7[time_log_counter] = kdtree_size_st;                 // kdtree初始大小s_plot8[time_log_counter] = kdtree_size_end;                // kdtree结束大小s_plot9[time_log_counter] = aver_time_consu;                //平均消耗时间s_plot10[time_log_counter] = add_point_size;                //添加点数量time_log_counter++;printf("[ mapping ]: time: IMU + Map + Input Downsample: %0.6f ave match: %0.6f ave solve: %0.6f  ave ICP: %0.6f  map incre: %0.6f ave total: %0.6f icp: %0.6f construct H: %0.6f \n", t1 - t0, aver_time_match, aver_time_solve, t3 - t1, t5 - t3, aver_time_consu, aver_time_icp, aver_time_const_H_time);ext_euler = SO3ToEuler(state_point.offset_R_L_I);fout_out << setw(20) << Measures.lidar_beg_time - first_lidar_time << " " << euler_cur.transpose() << " " << state_point.pos.transpose() << " " << ext_euler.transpose() << " " << state_point.offset_T_L_I.transpose() << " " << state_point.vel.transpose()<< " " << state_point.bg.transpose() << " " << state_point.ba.transpose() << " " << state_point.grav << " " << feats_undistort->points.size() << endl;dump_lio_state_to_log(fp);}}status = ros::ok();rate.sleep();}/**************** save map ****************//* 1. make sure you have enough memories/* 2. pcd save will largely influence the real-time performences **/if (pcl_wait_save->size() > 0 && pcd_save_en){string file_name = string("scans.pcd");string all_points_dir(string(string(ROOT_DIR) + "PCD/") + file_name);pcl::PCDWriter pcd_writer;cout << "current scan saved to /PCD/" << file_name << endl;pcd_writer.writeBinary(all_points_dir, *pcl_wait_save);}fout_out.close();fout_pre.close();if (runtime_pos_log){vector<double> t, s_vec, s_vec2, s_vec3, s_vec4, s_vec5, s_vec6, s_vec7;FILE *fp2;string log_dir = root_dir + "/Log/fast_lio_time_log.csv";fp2 = fopen(log_dir.c_str(), "w");fprintf(fp2, "time_stamp, total time, scan point size, incremental time, search time, delete size, delete time, tree size st, tree size end, add point size, preprocess time\n");for (int i = 0; i < time_log_counter; i++){fprintf(fp2, "%0.8f,%0.8f,%d,%0.8f,%0.8f,%d,%0.8f,%d,%d,%d,%0.8f\n", T1[i], s_plot[i], int(s_plot2[i]), s_plot3[i], s_plot4[i], int(s_plot5[i]), s_plot6[i], int(s_plot7[i]), int(s_plot8[i]), int(s_plot10[i]), s_plot11[i]);t.push_back(T1[i]);s_vec.push_back(s_plot9[i]);s_vec2.push_back(s_plot3[i] + s_plot6[i]);s_vec3.push_back(s_plot4[i]);s_vec5.push_back(s_plot[i]);}fclose(fp2);}return 0;
}

前面获取的传播状态 $\hat{x_k}$ 和协方差 $\hat{P_k}$ 对未知状态 $x_k$ 施加了一个先验高斯分布。具体来说， $\hat{P_k}$ 表示以下误差状态的协方差:
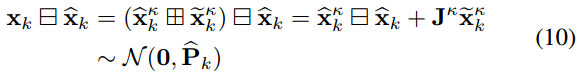
在这里插入图片描述
式中，Jκ为 $\widehat {x}_ {k}^ {\pi } 田 \widehat {x}_ {k}^ {\kappa } )日 \widehat {x} k$ 对 $\hat{x}^k_k$ =0处的偏微分。

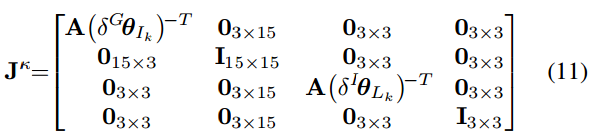
式中， $A(.)^{-1}$ 定义于公式(6)，如下。

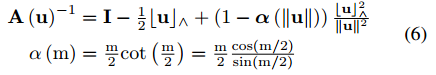
如下的 $δ^Gθ_{I_k}$ 和 $δ^Iθ{L_k}$ 分别为IMU的姿态和转动的误差状态。

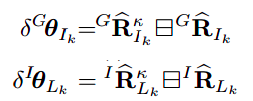
在这里插入图片描述
对于第一次迭代（以拓展的卡尔曼滤波器为例），有 $\hat{x^κ_k} =x_k$ , $J_κ =I$ 。

除了先验分布外，我们也有一个源于测量(8)的状态分布：
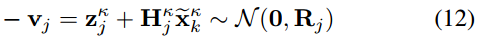
在这里插入图片描述
结合(10)的先验分布和(12)的测量模型，可得到状态 $x_k$ 的后验分布，其等价表示为 $x^k_k$ 及其最大后验估计:

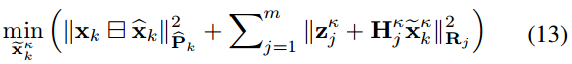
式中，有 $||x||^2_M = x^TM^{−1} x$ 。该最大后验估计问题可由下面的迭代卡尔曼滤波器解决：

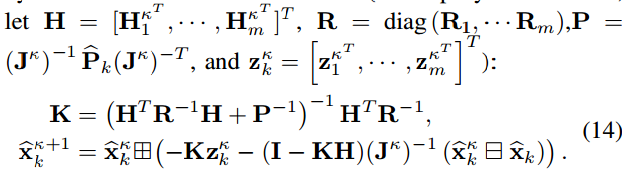
需注意，卡尔曼增益K计算需要对状态维数矩阵求逆，而不是在之前的工作中使用的测量维数矩阵。上述过程将重复进行，直到收敛(即 $||x_κ^{(k+1)} 日 x^κ_k||<$ 无穷小)。收敛后的最优状态和协方差估计为:
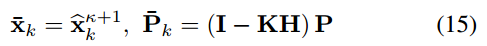
在这里插入图片描述
通过状态更新 $x_k$ ，第k次扫描中的每个LiDAR点(Lpj)将通过(16)被转换到全局框架:

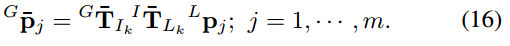
转换后的LiDAR点{Gp¯j}将被插入到由ikd-Tree表示的映射中。我们的状态估计在算法1中进行了总结。