10.3 反双曲函数

反三角函数中的 ar 代表 arc（弧）【详见本人另一博客中 2.2 描述的三角函数的定义】
反双曲函数中的 ar 代表 area（面积）【详见本人另一博客中 9.7.0 描述的对双曲函数的定义】

双曲函数详见本人另一篇博客：指数函数、对数函数、双曲函数

下图来自 Wikipedia

下图来自 Wikipedia

10.3.1 反双曲正弦函数【 y=arsinh(x) 】

$y=sinh(x)$ 通过 $y=x$ 镜像得到 $y=arsinh(x)$

反双曲正弦函数图像

反双曲正弦函数的指数形式

反双曲正弦函数的对数形式推导

反双曲正弦函数的导数推导

10.3.2 反双曲余弦函数【 y=arcosh(x) 】

通过限制定义域来使其满足水平线检验

$y=cosh(x)$ 通过 $y=x$ 镜像得到 $y=arcosh(x)$

反双曲余弦函数图像

反双曲余弦函数的指数形式

反双曲余弦函数的对数形式推导

反双曲余弦函数的导数推导

10.3.3 反双曲正切函数【 y=artanh(x) 】

$y=tanh(x)$ 通过 $y=x$ 镜像得到 $y=artanh(x)$

反双曲正切函数图像

反双曲正切函数的指数形式

反双曲正切函数的对数形式推导

反双曲正切函数的导数推导

10.3.4 反双曲余切函数【 y=arcoth(x) 】

$y=coth(x)$ 通过 $y=x$ 镜像得到 $y=arcoth(x)$

反双曲余切函数图像

反双曲余切函数的指数形式

反双曲余切函数的对数形式推导

反双曲余切函数的导数推导

10.3.5 反双曲正割函数【 y=arsech(x) 】

通过限制定义域来使其满足水平线检验

$y=sech(x)$ 通过 $y=x$ 镜像得到 $y=arsech(x)$

反双曲正割函数图像

反双曲正割函数的指数形式

反双曲正割函数的对数形式推导

反双曲正割函数的导数推导

10.3.6 反双曲余割函数【 y=arcsch(x) 】

$y=csch(x)$ 通过 $y=x$ 镜像得到 $y=arcsch(x)$

反双曲余割函数图像

反双曲余割函数的指数形式

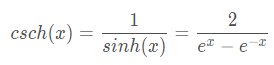
反双曲余割函数的对数形式推导

反双曲余割函数的导数推导