1 缘起
有一次偶然间听到有同事在说某个项目中使用了布隆过滤器,
哎呦,我去,我竟然不知道啥是布隆过滤器,
这我哪能忍?其实,也可以忍,但是,可能有的面试官不能忍!!!
于是,查询了布隆过滤器的相关知识,
特分享如下,帮助读者轻松应对知识交流与考核。
Wiki文档:https://en.wikipedia.org/wiki/Bloom_filter#Probability_of_false_positives
2 布隆过滤器
布隆过滤器是一种空间有效(Space efficient)的概率型数据结构。
是Burton Howard于1970年提出的,用于测试元素是否存在于某个集合。
这里有假阳性(误判,可能存在)和假阴性(正确判断,一定不存在)两个概念,
假阳性标识元素可能存在于集合中;
假阴性标识元素一定不存在于集合中;
需要注意的是,元素添加到布隆过滤器后,不可删除(可以通过计数布隆过滤器变量解决),
添加的元素越多,误判率越高。
因为使用“常规”无错hash技术处理大量源数据需要消耗大量内存,所以Bloom提出了一种处理技术。
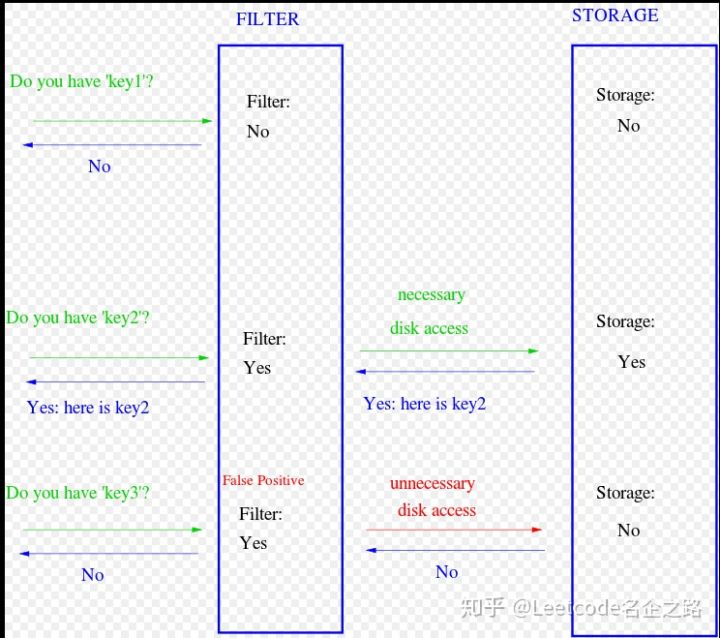
他举了一个50万单词断字算法的例子,90%的数据遵循简单的断字规则,10%的需要昂贵的磁盘访问才能检索特定的断字模式。
有了足够的核心内存,可以使用无错hash消除不必要的磁盘访问,有限的核心中,虽然Bloom技术使用了较小的hash区域,
但依旧消除了大多数不必要的访问。比如,只需理想无错hash 15%的hash区域即可消除85%的磁盘访问。
对于1%的假阳性概率,每个元素至少小于10bit,与集合中元素的大小或数量无关。
空的布隆过滤器是一个m位的位数组,全部置为0.
同时,需要定义k个不同的hash函数,每个hash函数将集合元素映射或hash到m个数组的位置,从而生成统一的随机分布。
一般,k是一个小常数,这取决于期望的错误率ε,而m与k和要添加的元素数量成比例。
设计k个不同的hash函数对于大k而言是不允许的。
对于较大范围输出的优秀hash函数而言,hash不同的字段几乎是没有相关性的,
因此,这种类型的hash可以将输出分为多个位字段来生成多个不同的hash函数(字段不同,hash结果大概率不同,因此等价于不同的hash函数)。
或者,将k个具有不同初始值(如0,1,…,k-1)元素传给hash函数;或者将这些值附加到键上。
对于较大的m或k,可以扩大hash函数的独立性,假阳性(误判)的概率可以忽略不计。
Dillinger & Manolios展示了使用增强hash和三次hash来推导k个索引的有效性,双hash的变体是有效的简单随机数生成器(使用两个或三个hash值作为种子)。
布隆过滤器中的元素是无法移除(删除)的,因为无法确定这个位置的数据是否真的应该删除,
为什么会这样?因为,删除元素时需要将元素映射在布隆过滤器数组值置为0,
所以,就有可能将已存在元素的数组值给误替了,导致已存在元素反而被误删了
(核心问题:无法确定要删除的元素是否一定在布隆过滤器中,元素a和元素b可能有某个hash值重合,所以,会出现这个问题,这也就阻止了想用计数方式存储数据的方案了,相同位置+1,但是布隆过滤器数组中的值只有0和1)。
可以通过第二层布隆过滤器模拟删除元素的操作,
第二个布隆过滤器存储删除的元素,不过,这种方式无法重新添加已元素到布隆过滤器中,
因为第二个布隆过滤器已经存在这个元素了,必须从第二个布隆过滤器中删除才行。
一般,所有键都是可用的,但是枚举(遍历)是非常昂贵的(如需要更多的磁盘空间)。
当假阳性(误判)比例过高时,可以重建布隆过滤器,不过这是非常少见的。
2.1 空间和时间优势
虽然布隆过滤器有误报的风险,但是,相对于其他集合(如自平衡二叉树、Trie树、哈希表、简单数组或链表)而言,布隆过滤器有较大的空间优势。
其中大多数数据结构至少需要存储数据项本身,这样通常需要的存储空间会从几个bit(如小整数)到任意bit(如字符串),而trie则是一个例外,因为它们可以共用相同的前缀。
而布隆过滤器不需要存储数据项,因此需要为实际存储提供单独的解决方案。
链表结构需要为指针提供额外的存储空间。
相反,布隆过滤器1%的误差和最佳k次hash的每个元素只需9.6bit,不论元素有多大。
这种优势部分来自于布隆过滤器的紧凑性,继承了数组的特性,另一部分来源于概率模型,1%的假阳性(误判)可以通过为每个元素仅增加4.8bit而减少10倍。
如果潜在值的数量很小,并且其中许多值可以在集合中,那么布隆过滤器相关优势容易被确定性位阵列超越,
确定性位阵列只需每个潜在元素的1bit。如果hash表开始忽略冲突并只存储每个每个桶是否含有元素,那么,hash表将有空间和时间上的优势。这种情况下,实际上就是k=1的布隆过滤器。
布隆过滤器的特殊属性如向集合中添加或检查元素的时间是常量:O(k),与集合中的元素数量是无关的。
其他恒定空间的数据结构则没有这个特性,但是,稀疏hash表的平均访问时间在实际应用中可以比布隆过滤器少。
然而,在硬件实现中,布隆过滤器则非常优秀,因为他的k个查找是独立的,可以并行执行。
为理解布隆过滤器的空间效率,将一般的布隆过滤器与k=1的特殊布隆过滤器相比是非常有用的。
k=1时,为了保持较低的假阳性(误判率),应该配置小分位,这也意味着数组必须非常大,并且包含长串的0.
数组的内容量相对于尺寸是非常低的(内容可以很少,但是可以消耗更多数组位置)。
广义上布隆过滤器(k>1)允许配置更多的bit,同时保持较低的假阳性(误判率),如果k和m配置合适,会有一般的位置被正确利用,
并且这些bit都是随机分配的,从而最小化冗余,最大化信息内容。
2.2 解决什么问题?
判断一个元素是否存在于某个集合中,有一定的误判率。
本文对误判率进行数学推导,详见后文。
2.3 判断原则?
某个元素不在集合中,则该集合一定不存在这个元素;
某个元素在集合中,则该集合可能存在这个元素,存在判断误差;
2.4 如何插入数据?
这个要从布隆过滤器的构成说起,布隆过滤器是由一个很长的bit数组和一系列hash函数组成,数组中的每个元素都只占1bit空间,每个元素值只能是0或1。布隆过滤器有k个hash函数,当一个元素添加到布隆过滤器时,会用k个hash函数进行k次hash计算,得到k个hash值,根据得到的hash值,将数组对应标的值置为1,即hash的置为数组下标(索引)。
判断某个元素是否在布隆过滤器时,通用对该元素进行k次hash计算,根据得到的数组下表获取数组的值,当所有数组值为1时,判定元素可能存在于布隆过滤器。
2.5 为什么会有误判?
随着大量的数据添加到布隆过滤器,当一个不在布隆过滤器的元素进行hash计算后,根据得到的数组下标查询数据时,这些数据被其他元素在插入时置为1了,则会误判该元素存在于布隆过滤器。
hash冲突的原因。假设元素a和元素b具有相同的hash值,同时假定进行3次hash计算,hash值为1,2,3
将元素a插入了布隆过滤器,a[1]=a[2]=a[3]=1
元素b没有插入布隆过滤器,
当查询元素b时,经过hash计算,得到的数组下标为1,2,3,由于元素a将这些数据置为1,
则判断b元素存在于布隆过滤器,误判就出现了。
2.6 为什么不能删除元素
根据布隆过滤器的相关特性可知,
因为删除元素时无法确定这个位置的数据是否真的应该删除,
删除元素时需要将元素映射在布隆过滤器数组值置为0,
所以,就有可能将已存在元素的数组值给误替了,导致已存在元素反而被误删了
(核心问题:无法确定要删除的元素是否一定在布隆过滤器中,元素a和元素b可能有某个hash值重合,所以,会出现这个问题,这也就阻止了想用计数方式存储数据的方案了,相同位置+1,但是布隆过滤器数组中的值只有0和1)。
2.7 工作过程
下面来看一下Wiki:https://en.wikipedia.org/wiki/Bloom_filter#Probability_of_false_positives中介绍的布隆过滤器工作过程。
现构建长度为8的布隆过滤器(长度为8的数组)m=8,hash次数为3,k=3,
添加三个元素x、y和z,经过三次hash后,分别落在各自的数组位置,如下图所示,
由图可知,其他未插入元素的位置均为0,初始化时数组所有位置均置为0,当插入元素时,将hash后的位置置为1。
查询元素是否在布隆过滤器时,查询元素时,对元素进行k次hash,获取数组索引,查询对应的位值(0或1),
只有所有的位值为1,才判定元素可能存于布隆过滤器,即,只要查询元素通过hash后获取的数组值存在0,则一定不存在于布隆过滤器。
如查询元素w,进行k=3次hash后,获取的hash值对应的数组值含有0,所以,w不存在于布隆过滤器。

2.8 应用场景
(1)网页URL去重,避免爬取相同的URL;
(2)垃圾邮箱过滤;
(3)推荐系统:针对不希望重复推荐的场景,如文章推荐、广告推荐的非重复性推荐场景;
(4)解决缓存穿透:使用布隆过滤器,当不存在该数据时,直接返回,不会将大量请求涌入到持久层(如关系型数据库MySQL);
(5)秒杀系统:某些商品,一个ID只允许购买一次;
等等一系列需要判断元素是否存在的应用场景。
3 误判率数学推导过程
3.1 参数
m:布隆过滤器长度
n:已添加的元素数量
k:hash的次数
3.2 误判率
布隆过滤器某个位不置为1的概率:
1 − 1 m 1-{\frac {1}{m}} 1−m1
哈希k次某个位置不置为1的概率:
( 1 − 1 m ) k \left(1-{\frac {1}{m}}\right)^{k} (1−m1)k
根据极限:
lim m → ∞ ( 1 − 1 m ) m = 1 e {\displaystyle \lim _{m\to \infty }\left(1-{\frac {1}{m}}\right)^{m}={\frac {1}{e}}} m→∞lim(1−m1)m=e1
有:
( 1 − 1 m ) k = ( ( 1 − 1 m ) m ) k / m ≈ e − k / m {\displaystyle \left(1-{\frac {1}{m}}\right)^{k}=\left(\left(1-{\frac {1}{m}}\right)^{m}\right)^{k/m}\approx e^{-k/m}} (1−m1)k=((1−m1)m)k/m≈e−k/m
添加n个元素某个位置不置为1的概率:
( 1 − 1 m ) k n ≈ e − k n / m {\displaystyle \left(1-{\frac {1}{m}}\right)^{kn}\approx e^{-kn/m}} (1−m1)kn≈e−kn/m
添加n个元素某个位置置为1的概率:
1 − ( 1 − 1 m ) k n ≈ 1 − e − k n / m {\displaystyle 1-\left(1-{\frac {1}{m}}\right)^{kn}\approx 1-e^{-kn/m}} 1−(1−m1)kn≈1−e−kn/m
k次hash后误判的概率为:不应置1的置为1的概率
(某个元素判定:k个hash位:全为0一定不存在,全为1可能存在,因此,置为1是可能的概率,因为最初状态全部置为0)
ε = ( 1 − [ 1 − 1 m ] k n ) k ≈ ( 1 − e − k n / m ) k {\displaystyle \varepsilon =\left(1-\left[1-{\frac {1}{m}}\right]^{kn}\right)^{k}\approx \left(1-e^{-kn/m}\right)^{k}} ε=(1−[1−m1]kn)k≈(1−e−kn/m)k
由误判率公式可知,当n增加时,误判率增加,m增加时,误判率减少。
下面推导一下hash次数与误判率的关系,令:
f ( k ) = ( 1 − e − k n / m ) k f(k)=\left(1-e^{-kn/m}\right)^{k} f(k)=(1−e−kn/m)k
等式两边取ln对数,有:
l n ( f ( k ) ) = k ∗ l n ( 1 − e − k n / m ) k ln(f(k))=k*ln\left(1-e^{-kn/m}\right)^{k} ln(f(k))=k∗ln(1−e−kn/m)k
求导:
1 f ( k ) f ′ ( k ) = l n ( 1 − e − k n / m ) k + − k n m e − k n / m 1 − e − k n / m \frac{1}{f(k)}f^{'}(k)=ln\left(1-e^{-kn/m}\right)^{k}+\frac{-k\frac{n}{m}e^{-kn/m}}{1-e^{-kn/m}} f(k)1f′(k)=ln(1−e−kn/m)k+1−e−kn/m−kmne−kn/m
若 f ′ ( k ) = 0 f^{'}(k)=0 f′(k)=0,有:
− k n m e − k n / m = ( 1 − e − k n / m ) l n ( 1 − e − k n / m ) k -k\frac{n}{m}e^{-kn/m}=(1-e^{-kn/m})ln\left(1-e^{-kn/m}\right)^{k} −kmne−kn/m=(1−e−kn/m)ln(1−e−kn/m)k
转化一下形式,有:
e − k n / m l n ( e − k n / m ) = ( 1 − e − k n / m ) l n ( 1 − e − k n / m ) k e^{-kn/m}ln(e^{-kn/m})=(1-e^{-kn/m})ln\left(1-e^{-kn/m}\right)^{k} e−kn/mln(e−kn/m)=(1−e−kn/m)ln(1−e−kn/m)k
于是,有:
e − k n / m = 1 − e − k n / m e^{-kn/m}=1-e^{-kn/m} e−kn/m=1−e−kn/m
e − k n / m = 1 / 2 e^{-kn/m}=1/2 e−kn/m=1/2
k = m n l n 2 k=\frac{m}{n}ln2 k=nmln2
即, k = m n l n 2 k=\frac{m}{n}ln2 k=nmln2时,误差率 f ( k ) = ( 1 − e − k n / m ) k f(k)=\left(1-e^{-kn/m}\right)^{k} f(k)=(1−e−kn/m)k取得极值,由 f ( x ) = ( 1 − e − k ) k > 0 f(x)=\left(1-e^{-k}\right)^{k}>0 f(x)=(1−e−k)k>0可知,
(0, m n l n 2 \frac{m}{n}ln2 nmln2]时, f ′ ( k ) < 0 f^{'}(k)<0 f′(k)<0
( m n l n 2 , + ∞ \frac{m}{n}ln2, +\infty nmln2,+∞]时, f ′ ( k ) < 0 f^{'}(k)<0 f′(k)<0
由此可知,当 k = m n l n 2 k=\frac{m}{n}ln2 k=nmln2时是 f ( k ) f(k) f(k)的最小值,即误判率最小。
通过函数图像模拟不同情况的曲线:
f ( k ) = ( 1 − e − k ) k f(k)=\left(1-e^{-k}\right)^{k} f(k)=(1−e−k)k
f ( k ) = ( 1 − e − 2 k ) k f(k)=\left(1-e^{-2k}\right)^{k} f(k)=(1−e−2k)k
f ( k ) = ( 1 − e − 3 k ) k f(k)=\left(1-e^{-3k}\right)^{k} f(k)=(1−e−3k)k
这里取m=1,n分别为1,2,3,
函数曲线如下图所示,由图可知,
误差率(误判率)有最小值,并且,当n增加时,误判率增加,m增加时,误判率减少(控制变量法:hash次数相同)。
绘图工具网站:https://zh.numberempire.com/graphingcalculator.php

4小结
(1)布隆过滤器的误差率为: f ( k ) = ( 1 − e − k n / m ) k f(k)=\left(1-e^{-kn/m}\right)^{k} f(k)=(1−e−kn/m)k;
(2)布隆过滤器最小误判率对应的hash次数与布隆过滤器与数据插入量的关系: k = m n l n 2 k=\frac{m}{n}ln2 k=nmln2,其中,k为hash次数,m布隆过滤器长度,n插入数据量;
(3)当n增加时,误判率增加,m增加时,误判率减少。