分类 classification

在目前的机器学习工作中，最常见的三种任务就是：

1. 回归分析

2. 分类分析

3. 聚类分析

什么是「分类」

虽然我们人类都不喜欢被分类，被贴标签，但数据研究的基础正是给数据“贴标签”进行分类。类别分得越精准，我们得到的结果就越有价值。

分类是一个有监督的学习过程，目标数据库中有哪些类别是已知的，分类过程需要做的就是把每一条记录归到对应的类别之中。由于必须事先知道各个类别的信息，并且所有待分类的数据条目都默认有对应的类别。

分类分为两种：

1. 二元分类：当我们必须将给定数据分类为 2 个不同的类时。示例——根据一个人的特定健康状况，我们必须确定该人是否患有某种疾病。

2. 多类分类：类的数量超过2。例如——根据不同种类的花的数据，我们必须确定我们的观察属于哪个种类。

区分「聚类」与「分类」

分类的目的是为了确定一个点的类别，具体有哪些类别是已知的，常用的算法是 KNN (k-nearest neighbors algorithm)，是一种有监督学习。聚类的目的是将一系列点分成若干类，事先是没有类别的，常用的算法是 K-Means 算法，是一种无监督学习。

两者也有共同点，那就是它们都包含这样一个过程：对于想要分析的目标点，都会在数据集中寻找离它最近的点，即二者都用到了 NN (Nears Neighbor) 算法。

一维分类问题 1D Classifcation Problem

 

本例子中一共有8条数据，每条数据格式（花瓣长度，类别）。不难看出第一类花花瓣都小于4cm，第二类花花瓣都大于4cm。机器学习模型也会学到这个特征，进行预测。

对于连续的特征，一个明显的选择是高斯分布

首先了解机器学习中的特征类别：连续型特征和离散型特征

例子：连续特征 [4654.1313, 11, 0, 4564654, …]

离散特征[‘Ask’, ‘Jokes’, ‘politics’, ‘five’, ‘gaming’]

一元正态分布（一元高斯分布）

高斯函数的概率密度函数定义为

 

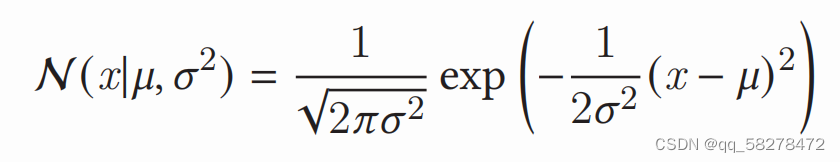
在数学中，连续型随机变量的概率密度函数是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。

数学期望为μ、方差为σ^2

 

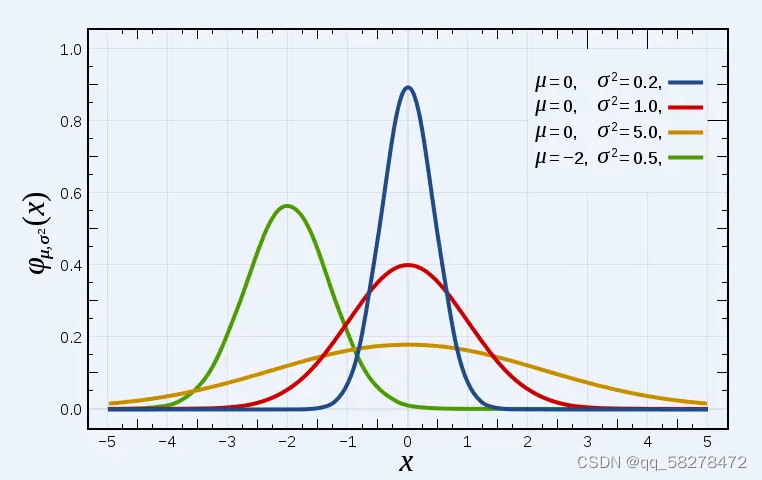
正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布,记为N（0，1)

正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线。正态曲线呈钟型，两头低，中间高，左右对称，曲线与横轴间的面积总等于1。

σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。

 

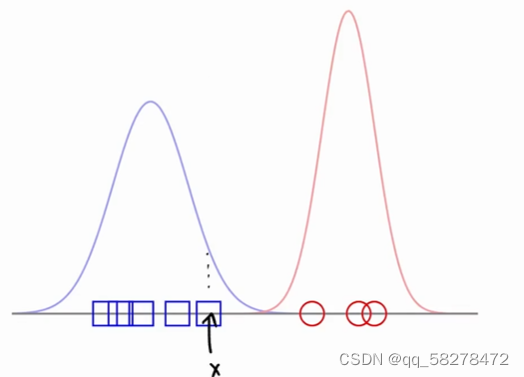
回到花卉分类问题，先把两类花卉近似看成高斯分布，并画出图像

 

对于一个新的测试数据点x，分别代入两个对应函数中去，哪个计算的输出最大，就分到其对应的类。

还可以测试数据点来自给定类的“可能性”有多大。可以相当于正确率去理解

 

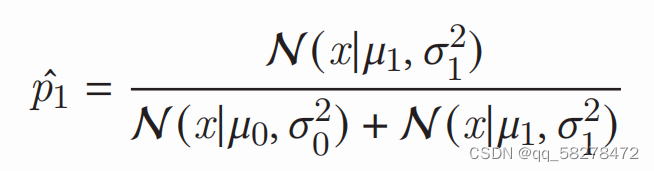
Adding ‘Prior’ Knowledge

这里想表达的就是我们可以在分类的时候加入一些先前的经验。例如，在邮件分类的问题中，大部分的邮件是正常的只有少量邮件是垃圾邮件；包括这个问题中，大部分的花卉属于是Class0，少部分的花卉属于Class1，我们想把我们观察到的经验告诉机器，提高准确率，因此我们可以加一些权重来控制这个事情。

 

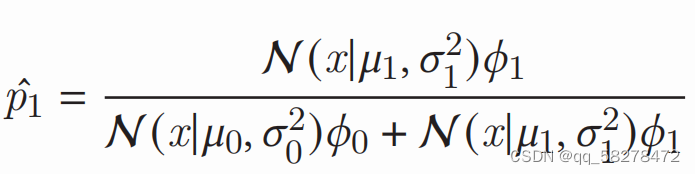
• We can encode this information as a weighting factor for each class, 𝜙0 and 𝜙1, where

𝜙1, 𝜙0 ∈ [0, 1] ，𝜙0 + 𝜙1 = 1 。如果两类别的数量差不多可以都取0.5。如果有一类更常见的话就把那类的参数设置更高就好。

这里其实加的这俩参数，就是所谓的先验知识，这个表达式就和贝叶斯分类任务类似，因此引出贝叶斯分类

贝叶斯

基本概念

1、先验概率 prior

先验概率仅仅依赖于主观上的经验估计，也就是事先根据已有的知识的推断，先验概率就是没有经过实验验证的概率，根据已知进行的主观臆测。

如抛一枚硬币，在抛之前，主观推断P（正面朝上） = 0.5。

2、后验概率

指某件事已经发生，想要计算这件事发生的原因是由某个因素引起的概率。比如一个人得了肺癌，想知道得肺癌由吸烟引起的概率（说白了后验概率实际上就是条件概率）后验概率和条件概率意思是一样的来自百度百科，事实上也确实一样

P (y|x)是y的后验分布，以x为条件

 

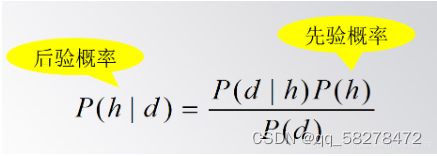
这个就是贝叶斯公式，反映了先验概率和后验概率的关系，后验概率P(h|d)是在数据d上得到的学习结果，反映了数据d的影响，这个学习结果是与训练数据相关的。 与此相反，先验概率是与训练数据d无关的，是独立于d的。

最大似然估计 Maximum Likelihood Estimation

拟合模型与数据的一种常用方法称为最大似然估计(Maximum Likelihood Estimation, MLE)。

极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。假设我们要统计全国人口的身高，首先假设这个身高服从服从正态分布，但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的身高，但是可以通过采样，获取部分人的身高，然后通过最大似然估计来获取上述假设中的正态分布的均值与方差。

最大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布的。

学生考试的成绩，根据既往的经验，我们可以假设学生的成绩是正态分布的，那么剩下的问题就是确定分布的期望和方差。所以，之所以要估计参数，是因为我们希望用较少的参数去描述数据的总体分布。而可以这样做的前提是我们对总体分布的形式是知晓的，只需要估计其中参数的值

之后就是推导了，取许多项的乘积会引起数值问题。为了克服这个问题，我们取不影响函数最大值的对数，然后最大化整体等价于最小化那个整体的负数，再用贝叶斯公式进行替换。

 

最开始由高斯分布近似出贝叶斯，右边那一项其实就是条件概率公式，所以应该也是服从高斯分布，视频里老师就是这个意思应该。如下所示：

 

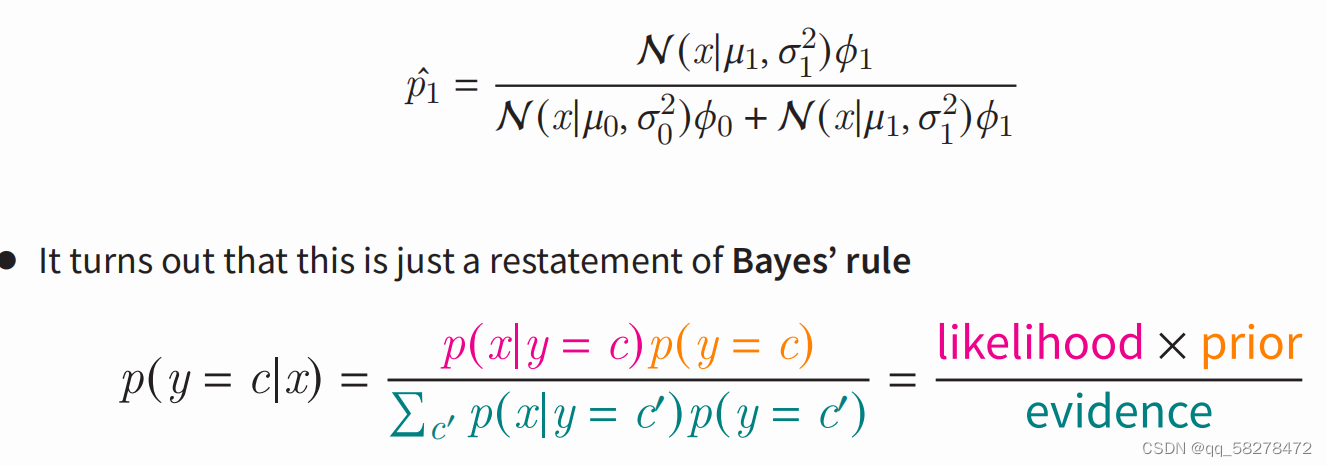
二项分布（伯努利分布）

说起二项分布(binomial distribution)，不得不提的前提是伯努利试验(Bernoulli experiment)，也即n次独立重复试验。伯努利试验是在同样的条件下重复、相互独立进行的一种随机试验。

伯努利试验的特点是：

（1）每次试验中事件只有两种结果：事件发生或者不发生，如硬币正面或反面，患病或没患病；

（2）每次试验中事件发生的概率是相同的，注意不一定是0.5；

（3）n次试验的事件相互之间独立。 举个实例，最简单的抛硬币试验就是伯努利试验，在一次试验中硬币要么正面朝上，要么反面朝上，每次正面朝上的概率都一样p=0.5，且每次抛硬币的事件相互独立，即每次正面朝上的概率不受其他试验的影响。如果独立重复抛n=10次硬币，正面朝上的次数k可能为0,1,2,3,4,5,6,7,8,9,10中的任何一个，那么k显然是一个随机变量，这里就称随机变量k服从二项分布

 

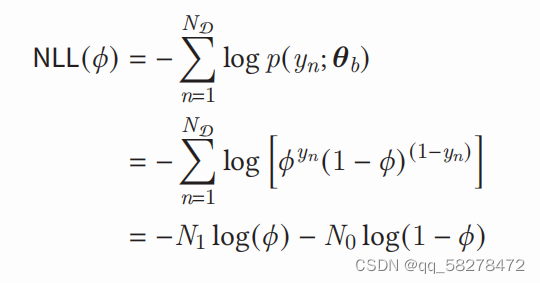
左边的那一部分化简，先把伯努利分布公式代入，在用对数公式展开log（ab）=loga+logb

其中N1，N0对应的是训练数据中，正负标签的总和。最后的结果对θ求偏导数就是结果，我求了半天没算出来。。。带log的忘了。

未完，待续。。。。。。。。