- 矩阵分块计算
A [ b 1 ⋯ b p ] = [ A b 1 ⋯ A b p ] A\left[\boldsymbol{b}_{1} \cdots \boldsymbol{b}_{p}\right]=\left[A \boldsymbol{b}_{1} \cdots A \boldsymbol{b}_{p}\right] A[b1⋯bp]=[Ab1⋯Abp]
[ ∣ ∣ a 1 ⋯ a n ∣ ∣ ] [ − b 1 − ⋮ − b n − ] = [ a 1 b 1 + ⋯ + a n b n ] \left[\begin{array}{ccc}| & & | \\ a_{1} & \cdots & a_{n} \\ | & & |\end{array}\right]\left[\begin{array}{ccc}- & b_{1} & - \\ & \vdots & \\ - & b_{n} & -\end{array}\right]=\left[a_{1} b_{1}+\cdots+a_{n} b_{n}\right] ⎣⎡∣a1∣⋯∣an∣⎦⎤⎣⎢⎡−−b1⋮bn−−⎦⎥⎤=[a1b1+⋯+anbn]
- 正交基的定义:
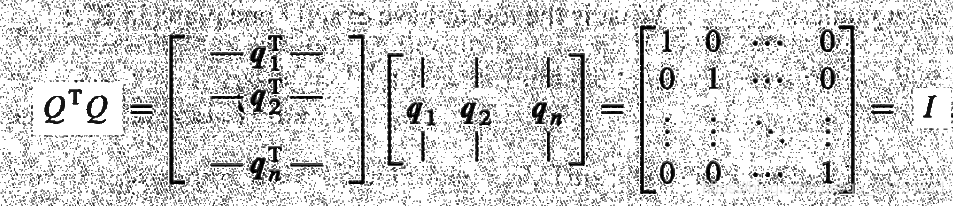












![第7章第23节:双图排版:两张图片的错位叠加 [PowerPoint精美幻灯片实战教程]](https://img-blog.csdnimg.cn/img_convert/87e41e879ec3f3aa957c46db991a64d0.png)