相关文章
线性代数（六）正交性
文章目录 一：内积、长度、正交性1.1内积1.2长度1.3正交向量1.4总结 二：正交集2.1定义2.2定理--正交基2.3正交投影2.4单位正交集 三：正交矩阵3.1单位正交列向量3.2性质3.3正交矩阵初入门 四：拉格姆-施密特方法4.1定义4.2步骤4.3例子…
施密特正交化(Gram-Schmidt Orthogonalization)
目录 1 Gram-Schmidt的计算公式推导2 Gram-Schmidt的意义3 Modified Gram-Schmidt (以算法模式计算正交向量)3.1 Modified G-S会出现的问题：当矩阵开始存在微小误差时，会在运算过程中不断累积误差，导致越算越不准确，以至于计算所得…
线性代数（9）：线性正交
一、正交向量组
（1）定义 若一个非零向量组中的向量两两相交，则称该向量组为正交向量组； 由单个非零向量组成的向量组也为正交向量组 （2）判断
1.2.1 方法 证明两两相交的的方法就是计算向量的内积和是否为…
两个图片叠加在一起css,css实现图片叠加的几种思路（记录笔记）
3、使用div层叠，设置两个div，一个position:relative;一个position:absolute; 就可以实现在div里面显示绝对定位，而不跑出div的层叠div，对于没有固定整个界面的width和height的情况适用。 如果界面的宽高都固定了像素值，…
学习如何使用html和css样式将两张图片叠加到另一张图片上，实现微信扫一扫二维码效果
学习如何使用html和css样式将两张图片叠加到另一张图片上，实现微信扫一扫二维码效果 <!DOCTYPE html>
<html>
<head><meta charset"utf-8"/><link rel"stylesheet" href"menuStyle.css"/><title>…
Matlab中实现两张图片的叠加显示效果
Matlab中实现两张图片的叠加显示效果 1、相同大小图片的叠加显示2、不同大小图片的叠加显示 ** 在matlab中以50%透明度实现两张图图片的叠加显示，图片的大小可以任意设置，不同大小的图片，较小的图片在整幅图中居中显示。** 1、相同大小图片的…
java中将两个图片进行叠加
有个需求要在一张图片上绘制图案，不好实现，就想到把图案的图片直接叠加到背景图片上，试了一下，居然成功了，话不多说，直接看代码：
public static void main(String[] args) {try {BufferedImage…
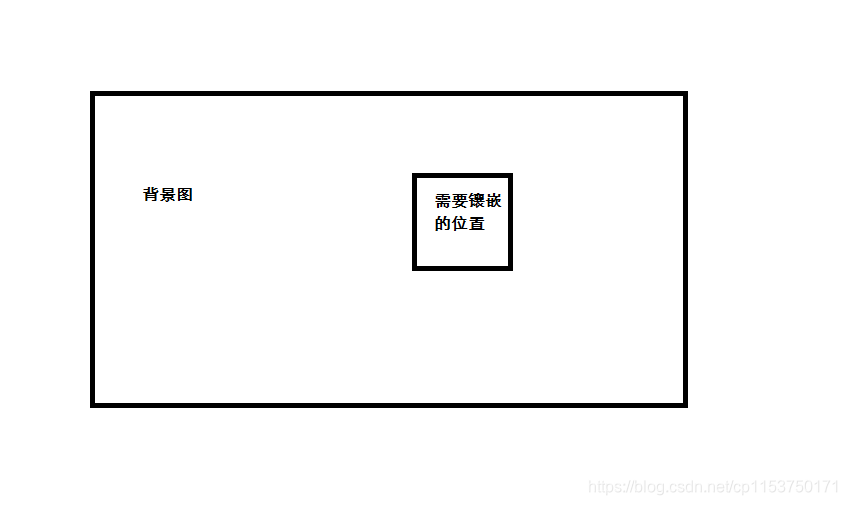
android 中关于两张图片叠加方法（记录）
最近在做一个小的Android项目中遇到一个问题，就是不知道为什么机器输出的分辨率不稳定，总是有几十个像素的误差。导致屏幕适配出现了问题。这次主要记录一下解决思路。 问题就如图 主要是一张背景图 ，在背景图指定区域去镶嵌一张指定图片。…
html盒子两个背景图片,css怎么实现两张图片叠加在一起,css添加盒子背景图片
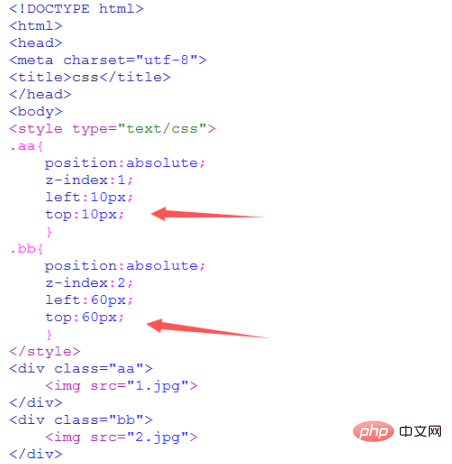
css怎么实现两张图片叠加在一起CSS怎么实现了两张图片的叠加，Css实现了两张图片叠加在一起的方法：可以通过分别设置div与页面左边缘的距离和div与页面上边缘的距离来实现。需要注意的是，两张图片都应该设置position:absolute属性。 环境&…
两个图片叠加在一起css,css两张图片怎么叠加在一起？
css实现两张图片叠加在一起的方法：首先添加2个img标签；然后设置它们的css样式为position:absolute；最后设置其中一个img样式为left:120px即可看见效果。 使用css把两个图片叠加，可以通过position定位属性设置两张图片的位置来实现…
使用Vue将两张图片叠加再保存为一张图片下载
最终效果
将一张课程图片和一张二维码图片叠加（网上图片随便乱找，勿对号入座！！！）
步骤
先将两张图片使用css进行叠加，然后按照自己需求将图片移动到合理位置要使用到一个插件将两张图片转为…
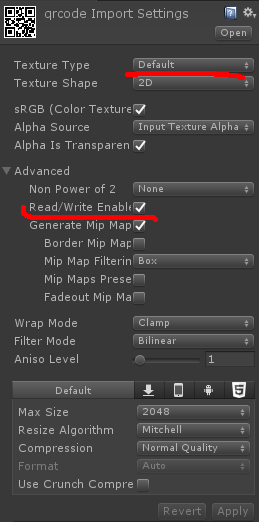
Unity-两张图片叠加合成一张图片
在做图片分享时，往往需要对图片加上水印或其他标签图片，这个时候就要考虑如何对多张图片进行叠加合成为一张图片。
其实一张图片就是一组单色像素组成的像素矩阵
要对两张图片进行叠加，只需要将背景图片中对应的像素颜色，替换成…
opencv两张图片叠加显示
详细流程： （一）、线性混合操作：使用addWeighted()1、代码2、说明3、图片效果 （二）、使用roi和mask方式1、代码2、说明3、图片效果 （一）、线性混合操作：使用addWeighted()…
html怎么使两张照片重叠,怎样把两张图片叠加在一起？
用手机后期的“双重曝光”功能，可以实现将两张图片叠加的效果，操作非常简单。比如：让人物剪影站在海面的效果 是由一张“海面背景图人物剪影”，两张图片合成： 为了让人物看上去更融入环境，后期加上“人物倒…
![第7章第23节：双图排版：两张图片的错位叠加 [PowerPoint精美幻灯片实战教程]](https://img-blog.csdnimg.cn/img_convert/87e41e879ec3f3aa957c46db991a64d0.png)
第7章第23节：双图排版：两张图片的错位叠加 [PowerPoint精美幻灯片实战教程]
本节演示图片错位叠加的排版方式，首先在此处按下并向左上方拖动，将图片移到另一张图片的上方。 在此处按下并向右下方拖动，以放大图片的尺寸，从而更容易形成图片叠加的效果。 接着来处理另一张图片。 在此处按下并向右下方拖动，将图片移到上面图片的右下方，并和上面的…
chatgpt赋能python：Python如何将两张图片叠加
Python如何将两张图片叠加
介绍
图像处理是计算机视觉领域的重要应用，而Python已经成为了图像处理中最流行的编程语言之一。在图像处理的过程中，有时需要将两张图片叠加在一起，这就需要用到Python中的图像叠加技术。
本文将介绍Python中如…
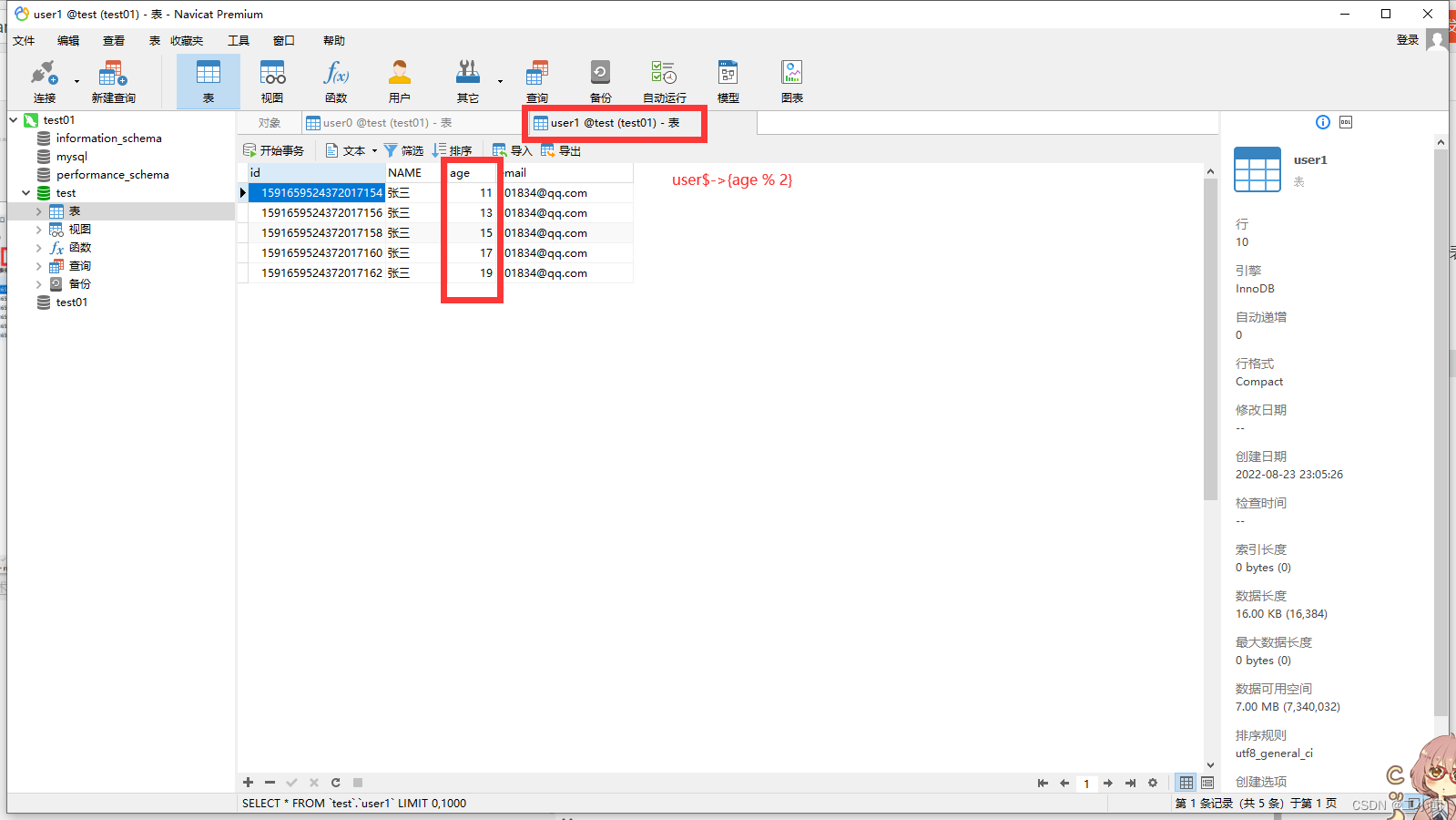
java 分表操作_Mybatis Plus 分表操作
大家都知道没到万不已就不分表分库，我也是没有办法，先不使用中间件实现简单的分表操作。可根据实际情况来分表，我现在要分的就是运动穿戴设备的运动数据，单次运动对应多个运动轨迹记录，有运动表(watch_sport)和运动详情表(watch_sport_detail)，数据量比较大的就是运动详情…
mysql年月分表_MySQL 按日期分表
一、表不存在时则创建 之前做项目实在是太赶了，很多东西都没记录。是时候补回来了 MySQL做一个大表，由于要存历史记录，所以数据量很大，查询很慢。恰好查询的时候，又不需要时间太久的冷数据。现在将其实现原理提取成一个…
ShardingJdbc分表
ShardingJdbc分表 前言一、ShardingJdbc分表1.引入maven依赖2.yml配置2.分表功能测试 总结 前言 ShardingJdbc官网 下载链接 快速入门 官网原话：
Apache ShardingSphere 是一套开源的分布式数据库解决方案组成的生态圈，它由 JDBC、Proxy 和 Sidecar&…