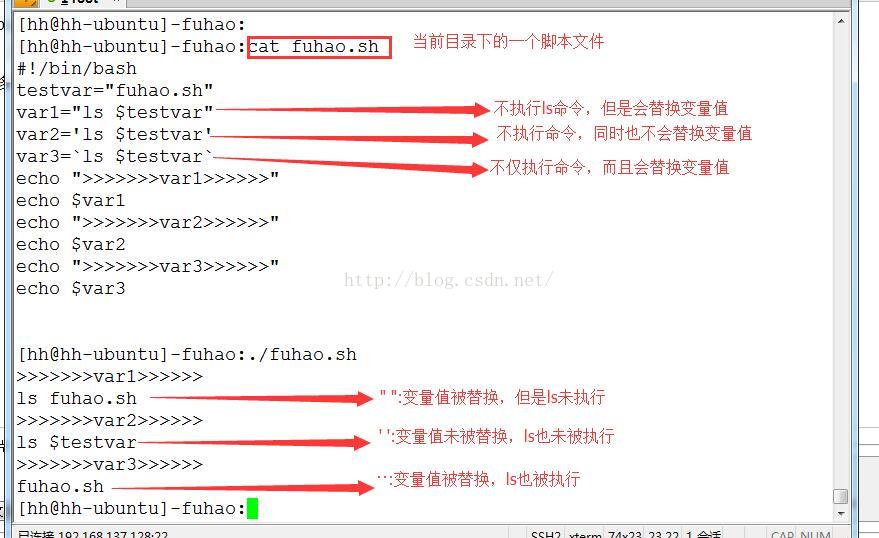
数字滤波器
- 一阶数字滤波器
- 时域分析
- 频域分析
- 数字化
- 代码示例
- 二阶巴特沃斯低通滤波器
- S域和Z域的频率关系分析
- 巴特沃斯滤波器举例说明
- 代码示例
声明:感谢知乎大佬的文章,原文链接
数字滤波器实现方法是把滤波器所要完成的运算编成程序并让计算机执行,也就是采用在代码的形式。
它面对的是离散时间的数字信号,是把输入序列通过一定的运算变换成输出序列。
问:如何将连续的模拟滤波器变成离散的数字滤波器?
答:双线性变换
S = 2 T s 1 − z − 1 1 + z − 1 = 2 f s 1 − z − 1 1 + z − 1 S = \frac {2} {Ts} \frac {1-z^{-1}} {1+z^{-1}} = 2fs\frac {1-z^{-1}} {1+z^{-1}} S=Ts21+z−11−z−1=2fs1+z−11−z−1
S域:复频域 Z域:极坐标系
一阶数字滤波器
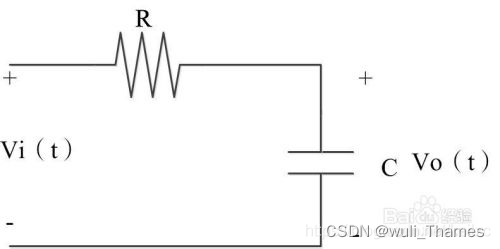
时域分析
电容
C = Q V (单位电压下器件所存储的电荷量) C = \frac Q V (单位电压下器件所存储的电荷量) C=VQ(单位电压下器件所存储的电荷量)
瞬时电流
I c = d Q d t (单位时间内通过的电荷数) Ic = \frac {dQ} {dt}(单位时间内通过的电荷数) Ic=dtdQ(单位时间内通过的电荷数)
代入得
I c = d ( C ∗ V ) d t Ic =\frac {d(C*V)} {dt} Ic=dtd(C∗V)
化简得
I c = C ∗ d U o d t Ic = C * \frac {dU_o} {dt} Ic=C∗dtdUo
根据基尔霍夫定律
U i = I c ∗ R + U o Ui = Ic*R + U_o Ui=Ic∗R+Uo
代入化简得
U i = R C ∗ d U o d t + U o Ui = RC * \frac {dU_o} {dt} + U_o Ui=RC∗dtdUo+Uo
d U o d t + U o R C = U i R C \frac {dU_o} {dt} + \frac {U_o} {RC} = \frac {U_i} {RC} dtdUo+RCUo=RCUi
根据微分公式
y ′ + p ( x ) y = q ( x ) y'+p(x)y = q(x) y′+p(x)y=q(x)
y = e − ∫ p ( x ) d x [ ∫ e ∫ p ( x ) d x q ( x ) + C ] y=e^{-\int p(x)dx}[\int e^{\int p(x)dx} q(x) + C] y=e−∫p(x)dx[∫e∫p(x)dxq(x)+C]
U o = e − ∫ 1 R C d t [ ∫ e ∫ 1 R C d t U i R C + C ] U_o=e^{-\int \frac {1} {RC}dt}[\int e^{\int \frac {1} {RC}dt} \frac {U_i} {RC} + C] Uo=e−∫RC1dt[∫e∫RC1dtRCUi+C]
U o = e − t R C [ U i R C ∫ e t R C d t + C ] U_o=e^{-\frac {t} {RC}}[ \frac {U_i} {RC} \int e^{\frac {t} {RC}dt} + C] Uo=e−RCt[RCUi∫eRCtdt+C]
其中
∫ e t d t = e t \int e^tdt = e^t ∫etdt=et
U o = e − t R C [ U i R C ∫ R C ∗ e t R C d t R C + C ] U_o=e^{-\frac {t} {RC}}[ \frac {Ui} {RC} \int RC* e^{\frac {t} {RC}d{\frac t {RC}}} + C] Uo=e−RCt[RCUi∫RC∗eRCtdRCt+C]
U o = e − t R C [ U i R C ∗ R C ∗ e t R C + C ] U_o=e^{-\frac {t} {RC}}[ \frac {Ui} {RC} * RC* e^{\frac {t} {RC}} + C] Uo=e−RCt[RCUi∗RC∗eRCt+C]
U o = C ∗ e − t R C + U i U_o= C*e^{-\frac {t} {RC}} + U_i Uo=C∗e−RCt+Ui
当 t = 0 时, U o = 0 , 得出 C = − U i 当t = 0时,U_o = 0,得出C=-U_i 当t=0时,Uo=0,得出C=−Ui
U o = ( 1 − e − t R C ) ∗ U i U_o= (1-e^{-\frac {t} {RC}})* U_i Uo=(1−e−RCt)∗Ui
频域分析
电容的阻抗
R = 1 j w C R = \frac {1} {jwC} R=jwC1
电压的传递函数
U o U i = 1 j w C R + 1 j w C \frac {U_o} {U_i} = \frac {\frac 1 {jwC}} {R + \frac 1 {jwC}} UiUo=R+jwC1jwC1
U o U i = 1 1 + j w R C \frac {U_o} {U_i} = \frac {1} {1 +jwRC} UiUo=1+jwRC1
化简
U o U i = 1 1 + ( w R C ) 2 − j w R C 1 + ( w R C ) 2 \frac {U_o} {U_i} = \frac {1} {1 + (wRC)^2} - j\frac {wRC} {1 + (wRC)^2} UiUo=1+(wRC)21−j1+(wRC)2wRC
对其取模得
( 1 1 + ( w R C ) 2 ) 2 + ( w R C 1 + ( w R C ) 2 ) 2 \sqrt { (\frac {1} {1 + (wRC)^2})^2 + (\frac {wRC} {1 + (wRC)^2})^2} (1+(wRC)21)2+(1+(wRC)2wRC)2
1 1 + ( w R C ) 2 \sqrt { \frac {1} {1 + (wRC)^2}} 1+(wRC)21
当 U o U i = 2 2 ,此时的频率为截止频率 当\frac {Uo} {Ui} = \frac {\sqrt 2} {2} ,此时的频率为截止频率 当UiUo=22,此时的频率为截止频率
2 2 = 1 1 + ( w R C ) 2 \frac {\sqrt 2} {2} =\sqrt { \frac {1} {1 + (wRC)^2}} 22=1+(wRC)21
w R C = 1 , w = 2 π f , 得出 2 π f R C = 1 wRC=1,w=2\pi f,得出 2\pi fRC=1 wRC=1,w=2πf,得出2πfRC=1
截止频率
f = 1 2 π R C f = \frac {1} {2\pi RC} f=2πRC1
数字化
H ( j w ) = U o U i = 1 1 + j w R C H(jw) =\frac {U_o} {U_i} = \frac {1} {1 +jwRC} H(jw)=UiUo=1+jwRC1
s = j w s=jw s=jw
H ( s ) = 1 1 + R C s H(s) =\frac {1} {1 +RCs} H(s)=1+RCs1
离散化 一阶后向差分进入Z变换
s = 1 − z − 1 T ( T : 采样周期) s = \frac {1-z^{-1}} {T} (T:采样周期) s=T1−z−1(T:采样周期)
H ( z ) = U o ( z ) U i ( z ) = 1 1 + R C 1 − z − 1 T H(z) = \frac {U_o(z)} {U_i(z)}=\frac {1} {1 +RC\frac {1-z^{-1}} {T}} H(z)=Ui(z)Uo(z)=1+RCT1−z−11
化简得
H ( z ) = U o ( z ) U i ( z ) = 1 1 + R C 1 − z − 1 T H(z) = \frac {U_o(z)} {U_i(z)}=\frac {1} {1 +RC\frac {1-z^{-1}} {T}} H(z)=Ui(z)Uo(z)=1+RCT1−z−11
U o ( z ) = T R C + T U i ( z ) + R C R C + T U o ( z ) z − 1 U_o(z)=\frac {T} {RC + T} U_i(z) + \frac {RC} {RC + T} U_o(z)z^{-1} Uo(z)=RC+TTUi(z)+RC+TRCUo(z)z−1
Z反变换得
U o ( n ) = T R C + T U i ( n ) + R C R C + T U o ( n − 1 ) U_o(n)=\frac {T} {RC + T} U_i(n) + \frac {RC} {RC + T} U_o(n-1) Uo(n)=RC+TTUi(n)+RC+TRCUo(n−1)
变换得
U o ( n ) = T R C + T U i ( n ) + ( 1 − T R C + T ) U o ( n − 1 ) U_o(n)=\frac {T} {RC + T} U_i(n) + (1- \frac {T} {RC + T} )U_o(n-1) Uo(n)=RC+TTUi(n)+(1−RC+TT)Uo(n−1)
令 A = T R C + T , U o ( n ) = A U i ( n ) + ( 1 − A ) U o ( n − 1 ) 令A= \frac{T} {RC + T} ,U_o(n)=AU_i(n)+(1-A)U_o(n-1) 令A=RC+TT,Uo(n)=AUi(n)+(1−A)Uo(n−1)
前面的频域得出
f = 1 2 π R C , 求得 R C = 1 2 π f f= \frac{1} {2\pi RC} ,求得RC= \frac{1} {2\pi f} f=2πRC1,求得RC=2πf1
从而得出
A = 1 1 + 1 2 π f T A= \frac{1} {1 + \frac {1}{2\pi fT}} A=1+2πfT11
此时将 A 代入 U o ( n ) 中 , 得到输入 U i 在截止频率 f 输出 U o 在数字域中的一阶滤波器表达式 此时将A代入Uo(n)中,得到 输入Ui 在截止频率 f 输出Uo在数字域中的一阶滤波器表达式 此时将A代入Uo(n)中,得到输入Ui在截止频率f输出Uo在数字域中的一阶滤波器表达式
U o ( n ) = 1 1 + 1 2 π f T U i ( n ) + ( 1 − 1 1 + 1 2 π f T ) U o ( n − 1 ) U_o(n)=\frac{1} {1 + \frac {1}{2\pi fT}}U_i(n)+(1-\frac{1} {1 + \frac {1}{2\pi fT}})U_o(n-1) Uo(n)=1+2πfT11Ui(n)+(1−1+2πfT11)Uo(n−1)
U o ( n ) = 1 1 + 1 2 π f T ( U i ( n ) − U o ( n − 1 ) ) + U o ( n − 1 ) U_o(n)=\frac{1} {1 + \frac {1}{2\pi fT}}(U_i(n)-U_o(n-1)) + U_o(n-1) Uo(n)=1+2πfT11(Ui(n)−Uo(n−1))+Uo(n−1)
代码示例
截止频率 f = 1Hz
thr_lpf+=(1 / (1 + 1/(2.0f * 3.14f * T )))*(height_thr - thr_lpf) ,其中T(采样周期)=1/采样频率
二阶巴特沃斯低通滤波器
S域和Z域的频率关系分析
对于s域来说,在模拟截止频率为 fa 时有:
S = j w a = j 2 π f a S=jw_a = j2 \pi f_a S=jwa=j2πfa
对于z域来说,在数字截止频率为 fd 的情况下
z = e s T , 其中 s = j w d , w d = 2 π f d , T = 1 f s z=e^{sT} ,其中s=jw_d ,w_d = 2 \pi f_d,T=\frac 1 f_s z=esT,其中s=jwd,wd=2πfd,T=f1s
z = e j 2 π f d f s z=e^{j2\pi \frac{f_d}{f_s}} z=ej2πfsfd
双线性变换
S = 2 T s 1 − z − 1 1 + z − 1 = 2 f s 1 − z − 1 1 + z − 1 S = \frac {2} {T_s} \frac {1-z^{-1}} {1+z^{-1}} = 2f_s\frac {1-z^{-1}} {1+z^{-1}} S=Ts21+z−11−z−1=2fs1+z−11−z−1
把这个数字截止频率为 fd 带入双线性变换公式可以得到:
S = 2 f s 1 − z − 1 1 + z − 1 = 2 f s 1 − e − j 2 π f d f s 1 + e − j 2 π f d f s = 2 f s e j 2 π f d f s − 1 e j 2 π f d f s + 1 S = 2f_s\frac {1-z^{-1}} {1+z^{-1}}=2f_s\frac{1-e^{-j2\pi \frac{f_d} {f_s}}} {1+e^{-j2\pi \frac{f_d}{f_s}}}=2f_s\frac{e^{j2\pi \frac{f_d} {f_s}}-1} {e^{j2\pi \frac{f_d}{f_s}}+1} S=2fs1+z−11−z−1=2fs1+e−j2πfsfd1−e−j2πfsfd=2fsej2πfsfd+1ej2πfsfd−1
运用下方的公式进行化简
e j x = c o s x + j s i n x e^{jx}=cosx + jsinx ejx=cosx+jsinx
e j A − e − j A e j A + e − j A = c o s A + j s i n A − ( c o s ( − A ) + j s i n ( − A ) ) c o s A + j s i n A + c o s ( − A ) + j s i n ( − A ) = j t a n A \frac{e^{jA}-e^{-jA}} {e^{jA}+e^{-jA}}=\frac{cosA+jsinA-(cos(-A)+jsin(-A))} {cosA+jsinA+cos(-A)+jsin(-A)}=jtanA ejA+e−jAejA−e−jA=cosA+jsinA+cos(−A)+jsin(−A)cosA+jsinA−(cos(−A)+jsin(−A))=jtanA
e j w − 1 e j w + 1 = e j w 2 e j w 2 ∗ e j w 2 − e − j w 2 e j w 2 + e − j w 2 = e j w 2 − e − j w 2 e j w 2 + e − j w 2 = j t a n w 2 \frac{e^{jw}-1} {e^{jw}+1} = \frac{e^{\frac{jw}{2}}} {e^{\frac{jw}{2}}} * \frac{e^{\frac{jw}{2}} - e^{-\frac{jw}{2}}} {e^{\frac{jw}{2}} + e^{-\frac{jw}{2}}} = \frac{e^{\frac{jw}{2}} - e^{-\frac{jw}{2}}} {e^{\frac{jw}{2}} + e^{-\frac{jw}{2}}}=jtan \frac{w}{2} ejw+1ejw−1=e2jwe2jw∗e2jw+e−2jwe2jw−e−2jw=e2jw+e−2jwe2jw−e−2jw=jtan2w
化简得
S = 2 f s e j 2 π f d f s − 1 e j 2 π f d f s + 1 = j 2 f s t a n π f d f s S=2f_s\frac{e^{j2\pi \frac{f_d} {f_s}}-1} {e^{j2\pi \frac{f_d}{f_s}}+1} = j2f_stan \frac{\pi f_d}{f_s} S=2fsej2πfsfd+1ej2πfsfd−1=j2fstanfsπfd
S = j 2 π f a = j 2 f s t a n π f d f s S=j2 \pi f_a= j2f_stan \frac{\pi f_d}{f_s} S=j2πfa=j2fstanfsπfd
f a = f s π t a n π f d f s f_a=\frac{f_s}{\pi}tan\frac{\pi f_d}{f_s} fa=πfstanfsπfd
模拟滤波器的角频率Wa
w a = 2 π f a = 2 π ∗ f s π t a n π f d f s = 2 f s t a n π f d f s w_a=2\pi f_a=2\pi*\frac{f_s}{\pi}tan\frac{\pi f_d}{f_s}=2f_stan\frac{\pi f_d}{f_s} wa=2πfa=2π∗πfstanfsπfd=2fstanfsπfd
去归一化只需要将模拟滤波器传递函数中的s进行如下替换
S = S w a S=\frac{S}{w_a} S=waS
得出用数字截止频率 fd 表示S的公式
S = 2 f s 1 − z − 1 1 + z − 1 2 f s t a n π f d f s = 1 − z − 1 1 + z − 1 t a n π f d f s S=\frac{2f_s\frac {1-z^{-1}} {1+z^{-1}}}{2f_stan\frac{\pi f_d}{f_s}}=\frac{\frac {1-z^{-1}} {1+z^{-1}}}{tan\frac{\pi f_d}{f_s}} S=2fstanfsπfd2fs1+z−11−z−1=tanfsπfd1+z−11−z−1
巴特沃斯滤波器举例说明
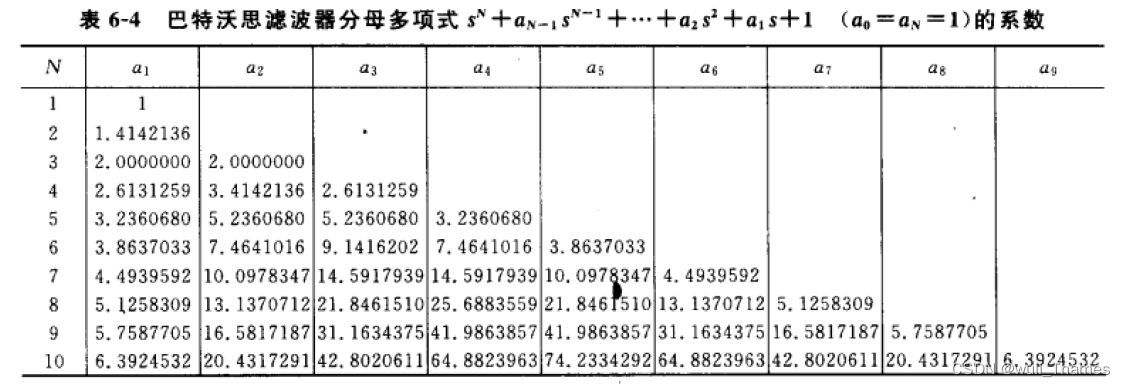
上表为巴特沃斯滤波器归一化(截止频率为 1 弧度 1 2 π ) 系数表,我们采用二阶 ( N = 2 ) 进行举例 上表为巴特沃斯滤波器归一化(截止频率为1弧度\frac 1 2\pi)系数表,我们采用二阶(N=2)进行举例 上表为巴特沃斯滤波器归一化(截止频率为1弧度21π)系数表,我们采用二阶(N=2)进行举例
H ( s ) = 1 S 2 + 1.414 S + 1 H(s)=\frac{1}{S^2 +1.414S+1} H(s)=S2+1.414S+11
H ( z ) = 1 ( 1 − z − 1 1 + z − 1 t a n π f d f s ) 2 + 1.414 ( 1 − z − 1 1 + z − 1 t a n π f d f s ) + 1 H(z)=\frac{1}{(\frac{\frac {1-z^{-1}} {1+z^{-1}}}{tan\frac{\pi f_d}{f_s}})^2+1.414(\frac{\frac {1-z^{-1}} {1+z^{-1}}}{tan\frac{\pi f_d}{f_s}})+1} H(z)=(tanfsπfd1+z−11−z−1)2+1.414(tanfsπfd1+z−11−z−1)+11
为方便化简将
Q = t a n π f d f s Q=tan\frac{\pi f_d}{f_s} Q=tanfsπfd
化简得
H ( z ) = Y ( z ) X ( z ) = Q 2 + 2 Q 2 z − 1 + Q 2 z − 2 ( 1 + 1.414 Q + Q 2 ) + ( 2 Q − 2 − 2 ) z − 1 + ( 1 + Q 2 − 1.414 Q ) z − 2 H(z)=\frac{Y(z)} {X(z)}=\frac{Q^2+2Q^2z^{-1}+Q^2z^{-2}} {(1+1.414Q+Q^2)+(2Q^{-2}-2)z^{-1}+(1+Q^2-1.414Q)z^{-2}} H(z)=X(z)Y(z)=(1+1.414Q+Q2)+(2Q−2−2)z−1+(1+Q2−1.414Q)z−2Q2+2Q2z−1+Q2z−2
再次为方便化简将
B 0 = Q 2 , B 1 = 2 Q 2 , B 2 = Q 2 , C = 1 + 1.414 Q + Q 2 , A 1 = 2 Q − 2 − 2 , A 2 = 1 + Q 2 − 1.414 Q B_0=Q^2,B_1=2Q^2,B_2=Q^2,C=1+1.414Q+Q^2,A_1=2Q^{-2}-2,A_2=1+Q^2-1.414Q B0=Q2,B1=2Q2,B2=Q2,C=1+1.414Q+Q2,A1=2Q−2−2,A2=1+Q2−1.414Q
化简得
H ( z ) = Y ( z ) X ( z ) = B 0 + B 1 z − 1 + B 2 z − 2 C + A 1 z − 1 + A 2 z − 2 H(z)=\frac{Y(z)} {X(z)}=\frac{B_0+B_1z^{-1}+B_2z^{-2}} {C+A_1z^{-1}+A_2z^{-2}} H(z)=X(z)Y(z)=C+A1z−1+A2z−2B0+B1z−1+B2z−2
Y ( z ) C + A 1 Y ( z ) z − 1 + A 2 Y ( z ) z − 2 = B 0 X ( z ) + B 1 X ( z ) z − 1 + B 2 X ( z ) z − 2 Y(z)C+A_1Y(z)z^{-1}+A_2Y(z)z^{-2}=B_0X(z)+B_1X(z)z^{-1}+B_2X(z)z^{-2} Y(z)C+A1Y(z)z−1+A2Y(z)z−2=B0X(z)+B1X(z)z−1+B2X(z)z−2
Y ( z ) = B 0 C X ( z ) + B 1 C X ( z ) z − 1 + B 2 C X ( z ) z − 2 − A 1 C Y ( z ) z − 1 − A 2 C Y ( z ) z − 2 Y(z)=\frac{B_0}{C}X(z)+\frac{B_1}{C}X(z)z^{-1}+\frac{B_2}{C}X(z)z^{-2}-\frac{A_1}{C}Y(z)z^{-1}-\frac{A_2}{C}Y(z)z^{-2} Y(z)=CB0X(z)+CB1X(z)z−1+CB2X(z)z−2−CA1Y(z)z−1−CA2Y(z)z−2
再再次为方便化简将
b 0 = B 0 C , b 1 = B 1 C , b 2 = B 2 C , a 1 = A 1 C , a 2 = A 2 C b_0=\frac{B_0}{C},b_1=\frac{B_1}{C},b_2=\frac{B_2}{C},a_1=\frac{A_1}{C},a_2=\frac{A_2}{C} b0=CB0,b1=CB1,b2=CB2,a1=CA1,a2=CA2
Y ( z ) = b 0 X ( z ) + b 1 X ( z − 1 ) + b 2 X ( z − 2 ) − a 1 Y ( z − 1 ) − a 2 Y ( z − 2 ) Y(z)=b_0X(z)+b_1X(z^{-1})+b_2X(z^{-2})-a_1Y(z^{-1})-a2Y(z^{-2}) Y(z)=b0X(z)+b1X(z−1)+b2X(z−2)−a1Y(z−1)−a2Y(z−2)
z : 表示当前周期, z − 1 : 表示上个周期, z − 2 : 表示上上个周期 z:表示当前周期,z^{-1}:表示上个周期,z^{-2}:表示上上个周期 z:表示当前周期,z−1:表示上个周期,z−2:表示上上个周期
代码示例
//二阶滤波器系数结构体
struct DoubleFilterFactor
{float b0;float b1;float b2;float a1;float a2;
}
//二阶滤波器暂存X,Y数据结构体
struct XYData
{float XData[2];float YData[2];
}void double IIRDoubleFilter(struct DoubleFilterFactor* facotr, struct XYData* xydata, float in)
{float y = facotr->b0*in + facotr->b1*xydata->XData[0] +facotr->b2*xydata->XData[1] +facotr->a1*xydata->YData[0] +facotr->a2*xydata->YData[0];//y表示输出信号xydata->XData[1] = xydata->XData[0];xydata->XData[0] = in;xydata->YData[1] = xydata->YData[0];xydata->YData[0] = y;return y;
}使用方式:
struct DoubleFilterFactor* tmpfactor;//对该二阶滤波器系数结构体赋值
struct XYData* tmpxydata;//无需赋值
int i;
float sample[num];//x表示输入信号
for(i = 0;i < num;i++)
{double Filterdata = IIRDoubleFilter(tmpfactor, tmpxydata, sample[i]);//Filterdata就是经过二阶滤波后的数据
}