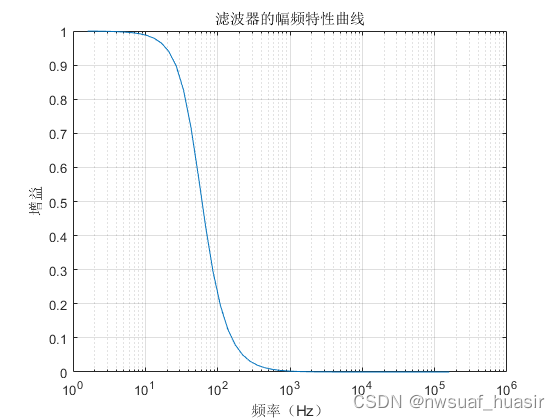
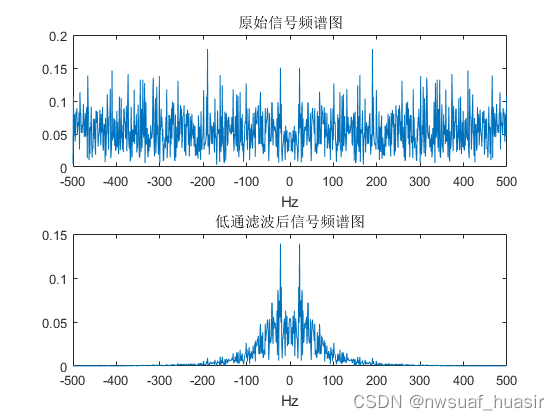
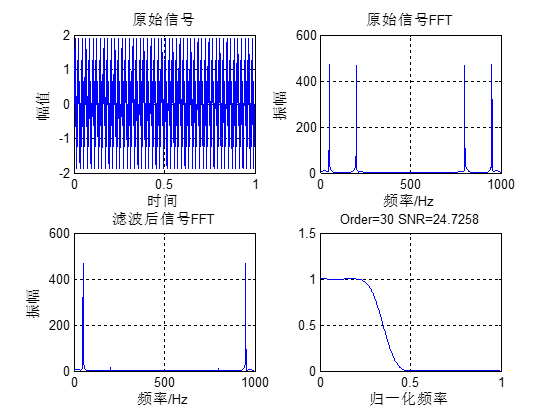
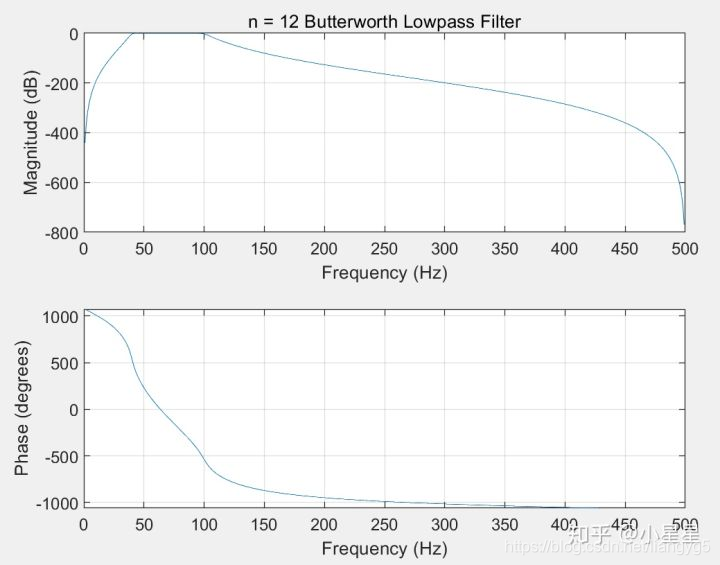
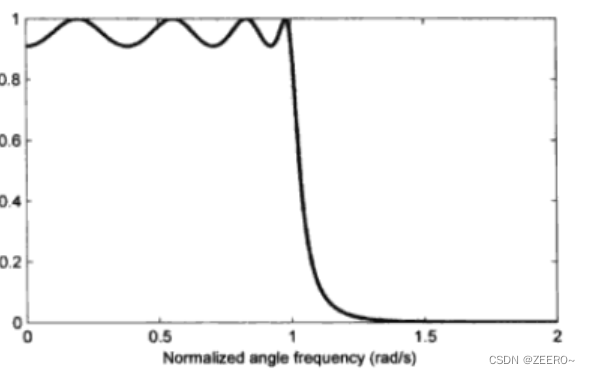
本例程展示了信号处理中低通滤波的作用,首先生成一个高斯白噪声,然后对其进行低通滤波。低通滤波器的截止频率和Q值可以自己设定,得到低通滤波器的传输函数后,在经过双线性变换法得到其单位脉冲响应。滤波后对原始信号的频谱和滤波后的信号的频谱进行了对比。
%% 低通滤波器演示程序
%% 生成白噪声信号
clc;clear all; close all;
N = 1000; %采样点数
fs = N; %采样频率
fre_base = -N/2:N/2-1;
a = randn(N,1); %生成符合高斯分布的随机噪声
F = fftshift((fft(a)))*2/N; %对其进行快速傅里叶变换
%% 生成低通滤波器
cut_off_freq = 50;
Q = 0.625;
plot_enable_L = 1;
[Hs, H_z] = produce_LPF(cut_off_freq, Q, fs, plot_enable_L);
%% 进行低通滤波
filterd_signal = filter(H_z.num{:}, H_z.den{:}, a);
filter_sig_f = fftshift(fft(filterd_signal))*2/N;
%% 绘图
figure;
subplot(2,1,1); %绘制子图
plot(fre_base,abs(F)); %绘制频率图
xlabel('Hz');
title('原始信号频谱图');
subplot(2,1,2); %绘制子图
plot(fre_base,abs(filter_sig_f)); %绘制频率图
xlabel('Hz');
title('低通滤波后信号频谱图');
产生低通滤波器的子函数代码如下:
function [Hs, H_z] = produce_LPF(cut_off_freq, Q, fs, plot_enable_L)
%% 构造低通滤波器w0 = 2*pi*cut_off_freq; % 滤波器截止频率对应的角频率A=1; B=w0/Q; C=w0^2; % 传递函数构造因子numerator = C; % 传递函数的分子的矩阵表示denominator = [A B C]; % 传递函数的分母的矩阵表示disp('二阶低通滤波器的传递函数');Hs = tf(numerator, denominator) % 构造模拟低通滤波器传递函数H_z = c2d(Hs, 1/fs, 'tustin'); % 将滤波器的脉冲响应用双线性变换法离散化%% 绘制图形 if plot_enable_L == 1%%计算坐标,画模拟滤波器的频率特性w = logspace(1,6); % 产生10^1到10^4次的对数坐标hs = freqs(numerator,denominator,w); % 滤波器的幅频、相频特性曲线mag = abs(hs); % 取幅值 phase = angle(hs); % 取相角f = w/(2*pi); % 将横坐标的单位由rad变为Hz phase = phase*180/pi; % 将纵坐标的单位变为度。figure; semilogx(f, mag); grid on xlabel('频率(Hz)'); ylabel('增益'); title('滤波器的幅频特性曲线');figure; semilogx(f, phase); grid on; xlabel('频率(Hz)'); ylabel('相位(°)'); title('滤波器的相频特性曲线');figure; impulse(Hs); grid on xlabel('时间'); ylabel('幅度'); title('模拟滤波器脉冲响应');figure; impz(H_z.num{:}, H_z.den{:}); grid on; %画双线性变换后的数字滤波器的脉冲响应 xlabel('点数'); ylabel('幅度'); title('数字滤波器脉冲响应');endend