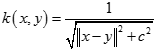核技巧Kernel trick

背景及含义：
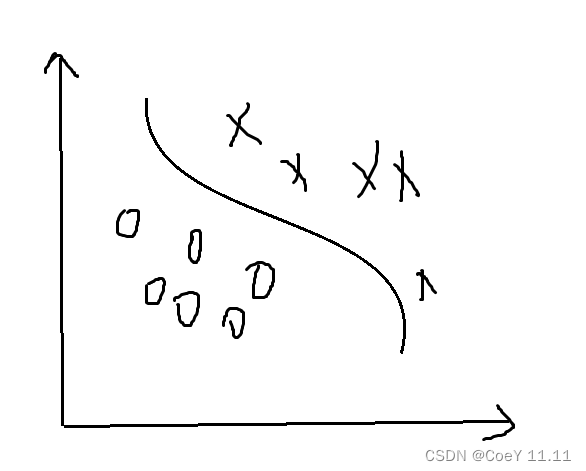
对于 原始样本空间内或许不存在能正确划分两类样本的超平面 问题，考虑 将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。
令$\varphi (x)$表示将x映射后的特征向量，则在求解特征空间中划分的超平面时，将原优化问题（支持向量机基本型）转化为求解对偶问题，将涉及到计算$\varphi (x_i{)}^T\varphi (x_j)$，即样本 $x_j$与$x_i$映射到特征空间之后的内积，由于特征空间维数可能很多，直接计算该内机会很困难，因此设想函数：(即用$\kappa (.,.)$直接表示内积结果)
$$\kappa (x_i,x_j)=<\varphi (x_i),\varphi (x_j)>=\varphi (x_i{)}^T\varphi (x_j)$$
则在特征空间中划分超平面对应的模型可表示为
$$f(x)=w^T\varphi (x)+b$$
什么函数可作为核函数：
由上可知，若已知映射$\varphi ()$，可给出核函数，但现实任务中常不知道$\varphi ()$的形式，而是直接使用核函数将原样本空间向高维映射，下面定理给出可作为核函数的条件：

令$\chi$为输入空间，$\kappa (.,.)$是定义在$\chi \times \chi$上的对称函数，则$\kappa$是核函数当且仅当对于任意数据 D = { x 1 , x 2 , . . . , x m } D=\{x_1,x_2,...,x_m\} D={x1​,x2​,...,xm​},核矩阵$K$总是半正定的：
$$K=[\kappa (x_i,x_j){]}_{(n\times n)}$$

只要一个对称函数对应的核矩阵半正定，它就能作为核函数使用，都能隐式的定义一个称“再生希尔伯特空间”的特征空间。

常用核函数及组合原则
常用核函数：

组合（${\kappa }_1$和${\kappa }_2$都为核函数）：

1. ${\gamma }_1{\kappa }_1+{\gamma }_2{\kappa }_2$仍为核函数
2. ${\kappa }_1⨂{\kappa }_2(x,z)={\kappa }_1(x,z){\kappa }_2(x,z)$核函数的直积也是核函数
3. $\kappa (x,z)=g(x){\kappa }_1(x,z)g(z)$也为核函数，任意函数g(x).

举例理解

根据阅读的知乎文章进一步理解：link

1. 核函数是在高维特征空间中的内积（可理解为相似度）
   对核函数$k(x,y)=<x,y{>}^2,x=(x_1,x_2),y=(y_1,y_2)$,该核函数对应的映射为$P(x,y)=(x^2,\sqrt{2}xy,y^2)$,即满足：
   $$<P(x),P(y)>=k(x,y)$$
   从这个例子中也可以看出用核技巧计算实际上是在原始的分类依据$x,y$上增添了$xy$的部分，相当于在分类中加入了综合考虑两个样本的部分.
2. 核矩阵中的元素定义了各样本点在高维空间中的相似度.

Mercer条件及其证明

核函数在应用过程中要注意的

1 函数的选择
比如： _{nngt的，忘了要举哪儿的例子了，果然啥事儿不能拖，想起来再补orz}
2 目前并没有研究说明对某种问题需要用某个核函数
（_{之前看到过一个椭圆形分界线，利用椭圆函数直接把核函数找出来的，感觉就很神奇，但是文献找不到了orz}）
回去查找更多的文献qaq

1 周志华. 机器学习 : = Machine learning[M]. 清华大学出版社, 2016.